
|
|
Свойства арифметических операций для транспонированных матриц.12 1) §3.Определитель квадратной матрицы и его свойства. Одной из важнейших характеристик квадратных матриц является ее определитель или детерминант: 1) Определитель второго порядка равен: 2) Определитель третьего порядка вычисляется по формуле
Таким образом, вычисление определителя третьего порядка свелось к вычислению трех определителей второго порядка. Каждый из них получается вычеркиванием строки и столбца, которые содержат элемент, стоящий перед этим определителем. Знаки перед слагаемыми вычисляются по формуле Утверждение. Определитель может быть разложен по любой строке или столбцу {б/д}. Перечислим без доказательства основные свойства определителей.
равен нулю.
Определение.Матрица, определитель которой равен нулю, называется вырожденной.
§4.Миноры и ранг матрицы. Рассмотрим матрицу Определение 1.Минором k – го порядка матрицы А (обозначается Мk) называется определитель, составленный из элементов, стоящих на пересечении выбранных k строк и столбцов матрицы А. Определение 2. Рангом матрицы А (rang(A)) называется максимальный порядок минора, отличного от нуля. Т.е., rang(A) = r, если 1) имеющий порядок r, называется базисным минором матрицы А. (Из определения сразу следует, что Строки и столбцы матрицы А, на которых строится базисный минор, так же называются базисными. Имеет место очень важное утверждение: Теорема о базисном миноре. Любая строка (столбец) матрицы А является линейной комбинацией базисных строк (столбцов). {б/д}
Любую матрицу Теорема 1. Ранг матрицы равен рангу системы векторов, составляющих эту матрицу. {Для определенности рассмотрим систему строк матрицы (S). Выберем произвольный базисный минор Mr . По предыдущей теореме любая строка матрицы, не принадлежащая базисным, линейно выражается через базисные. Следовательно, ее можно исключить из системы не изменив ранг самой системы (Введение, §4,Т.1). Отсюда получаем, что rang(S) ≤ r. Но, если ранг будет строго меньше r, то одна из строк базисного минора будет линейной комбинацией остальных и Mr = 0 (§3,св.5), что противоречит условию. Таким образом – rang(S) = rang(A)} Следствием Т.1для квадратных матриц является обобщение свойства 5 §3: Теорема 2.Определитель матрицы равен нулю тогда и только тогда, когда его строки (столбцы) линейно зависимы. {Необходимость. Пусть det(An) = 0 Достаточность. Строки линейно зависимы
§5.Вычисление ранга матрицы. Для вычисления ранга матрицы используется два метода. I. Метод окаймляющих миноров. Определение 1.Окаймляющими минорами некоторого фиксированного минора называются все миноры, полученные добавлением к нему дополнительного столбца и дополнительного строки данной матрицы ( Метод заключается в отыскании произвольного отличного от нуля минора и вычисления всех миноров, его окаймляющих. Если все эти миноры равны нулю, то ранг матрицы равен рангу исходного минора. В противном случае операция повторяется. Обоснованием метода служит Теорема 1.rang(A) = r, если II. Метод элементарных преобразований. Определение 2.Элементарными преобразованиями называются следующие: 1. Перестановка двух строк (столбцов). 2. Умножение строки (столбца) на число, отличное от нуля. 3. Прибавление к одной строке (столбцу) другой строки (столбца), умноженной на число. Теорема 2. Элементарные преобразования не меняют ранг матрицы. {При указанных преобразованиях любой минор матрицы (как обычный определитель) может изменить свое значение только следующим образом: Определение 3.Матрица В, полученная из А элементарными преобразованиями, называется эквивалентной А ( Определение 4.Первый ненулевой элемент строки будем называть отмеченным. Определение 5.Матрица называется ступенчатой, еслиотмеченныйэлемент каждой строки расположен правее отмеченногоэлемента предыдущей. Теорема 3.Любая матрица приводится к ступенчатому виду элементарными преобразованиями. {Доказательство носит конструктивный характер и будет продемонстрировано на примере} Пример. Привести матрицу к ступенчатому виду.
(в рамках −отмеченные элементы матрицы) Алгоритм может быть применен к любой матрице.
Теорема 4. Ранг ступенчатой матрицы равен числу ее ненулевых строк. {Снова продемонстрируем на том же примере: rang(A) = 3; в качестве базисного минора возьмем минор, составленный из строк 1,2,3 и столбцов 1,2,4: §6.Обратная матрица. Для квадратной матрицы важную роль играет понятие обратной матрицы. Определение 1.Матрицей, обратной матрице А (обозначается Теорема 1. Обратная матрица (если она существует) − единственна. {Пусть у матрицы А есть 2 обратных: В и С. Рассмотрим произведение ВАС: ВАС = (ВА)С = ЕС = С. С другой стороны ВАС = В(АС) = ВЕ = В. Отсюда В = С} Для вычисления обратной матрицы необходимо ввести еще несколько понятий. Легко заметить, что минор (n – 1) − го порядка у квадратной матрицы Аn можно определять, не задавая строки и столбцы, а, указав один элемент Определение 2.Алгебраическим дополнением элемента Из определения детерминанта матрицы An сразу следует, что определитель матрицы равен сумме произведений элементов любой строки (столбца) на алгебраические дополнения этой строки (столбца): С другой стороны, Т.е. сумма произведений элементов любой строки (столбца) на алгебраические дополнения другой строки (столбца) равна нулю. {Фактически, мы получаем определитель с двумя одинаковыми строками (столбцами)} Определение 3. Транспонированная матрица из алгебраических дополнений называется присоединенной матрицей: Теорема 2. {При умножении k −ой строки А на k − ый столбец Следствие. Пример. Найти обратную матрицу для
Замечания. 1. Полезно запомнить, что обратная матрица второго порядка получается из исходной следующим образом: элементы главной диагонали меняются местами, у элементов второй диагонали изменяется знак. Полученная матрица делится на определитель. 2. Обратная матрица может быть получена с помощью элементарных преобразований. Для этого составляется матрица
Свойства обратной матрицы. 1. 2. 3. В заключение докажем критерий существования обратной матрицы: Теорема 3.Обратная матрица {1. Пусть
§7.Решение матричных уравнений. Использование обратных матриц позволяет решать простые матричные уравнения относительно квадратных матриц. Рассмотрим пример одной из таких задач. Решить уравнение AXB + C = D, где Матрица Х равна:
Замечание. Так как умножение матриц не коммутативно, необходимо внимательно смотреть за тем, с какой стороны следует умножать правую часть на обратные матрицы.
§8. Системы линейных алгебраических уравнений (СЛАУ). Определение 1. Система уравнений линейных алгебраических уравнений с n неизвестными (сокращенно СЛАУ). Такая запись уравнений носит название координатной формы записи. Более компактной записью является матричная форма. Нетрудно видеть, что левая часть системы представляет собой вектор, полученный умножением матрицы системы неизвестных
системы может быть записано в виде Рассмотрим еще несколько общих понятий, относящихся к СЛАУ. Определение 2. СЛАУ называется совместной, если у нее существует хотя бы одно решение. Если решений не существует, система называется несовместной. Определение 3. СЛАУ, вектор правых частей которой равен нулю: однородной. В противном случае система называется неоднородной. Для однородных СЛАУ имеют место несколько общих утверждений. Теорема 1.Однородная СЛАУ всегда совместна. {Нулевой вектор всегда является решением однородной СЛАУ} Теорема 2.Множество решений однородной СЛАУ образует линейное пространство. {Пусть Замечание. Пространство решений однородной СЛАУ является, очевидно, подпространством линейного пространства n – мерных векторов
§9. Квадратные СЛАУ. Правило Крамера. Рассмотрим вначале СЛАУ с квадратной матрицей А − число уравнений равно числу неизвестных: Правило Крамера. Обозначим определитель матрицы буквой d , а определители матриц, полученных из А заменой k – го столбца столбцом правых частей Теорема(правило Крамера). Если определитель матрицы системы {
§10.Критерий совместности СЛАУ. Теорема Кронекера – Капелли. Вернемся к общим СЛАУ Определение.Матрица, составленная из коэффициентов при неизвестных и столбца правых частей, называется расширенной матрицей системы: Теорема(Кронекера – Капелли). СЛАУ совместна тогда и только тогда, когда ранг расширенной матрицы равен рангу исходной матрицы системы, т.е. {1. Система совместна. Правая часть есть линейная комбинация столбцов матрицы, коэффициенты которой равны координатам вектора решения. Т.е. 2.
§11.Общее решение СЛАУ. Определение.Множество решений системы линейных алгебраических уравнений называется общим решением этой системы. Т.е. любой вектор этого множества есть решение и любое решение этой системы принадлежит указанному множеству. Из §8 следует, что общим решением однородной системы является некоторое подпространство пространства {Нулевой вектор (0,0,…,0) не является решением исходной системы.} Итак, дана совместная система Можно показать, что любое решение может быть получено таким же образом. Достаточно взять В общем случае базисного минора будем называть неизвестные, не входящие в базисный минор, свободными, а, входящие в него – зависимыми. На практике матрицу системы сначала приводят к ступенчатому виду, затем выбирают базисный минор и , таким образом, зависимые и свободные неизвестные. При этом, желательно все преобразования производить только со строками, чтобы сохранить нумерацию неизвестных. После этого зависимые переменные выражают через свободные и записывают общее решение. Рассмотрим на примере данный алгоритм и сделаем несколько общих выводов.
Пусть
Из этого примера можно вывести несколько важных общих закономерностей. I. Ранг системы решений (S(x)) равен числу свободных неизвестных, т.е. rang(S(x)) = n – r, где n – количество неизвестных, а r – ранг матрицы системы (В примере: n = 4, r = 2, rang(S) = 2). Обычно, свободные неизвестные для каждого из решений выбираются следующим образом (для простоты будем считать для решения для решения ………………………………………………… для решения Легко видеть, что полученные решения 1) линейно независимы и 2) любое решение системы будет их линейной комбинацией.
II. Вектор описывает всю линейную оболочку решений однородной системы, т. е. − общее решениеоднородной системы уравнений.
III. Общее решение неоднородной системы равно сумме общего решения однородной системы и частного решения неоднородной:

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 . 2)
. 2) 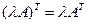 . 3)
. 3)  . {Слева – строки А на столбцы В и транспонирование. Справа – столбцы В на строки А , т.е. уже транспонированная.}
. {Слева – строки А на столбцы В и транспонирование. Справа – столбцы В на строки А , т.е. уже транспонированная.}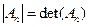 . Дадим рекуррентное определение этого понятия.
. Дадим рекуррентное определение этого понятия.

 , где i и j − индексы этого элемента. Данная формула называется разложением определителя по первой строке. Определитель четвертого порядка выражается по этому же правилу через определители третьего порядка и так далее.
, где i и j − индексы этого элемента. Данная формула называется разложением определителя по первой строке. Определитель четвертого порядка выражается по этому же правилу через определители третьего порядка и так далее.
 (определитель произведения равен произведению определителей)
(определитель произведения равен произведению определителей) . Выберем k произвольных строк и k произвольных столбцов этой матрицы (
. Выберем k произвольных строк и k произвольных столбцов этой матрицы (  ).
). , 2)
, 2)  Любой минор,
Любой минор, )
) r < n
r < n  ).
). {б/д}
{б/д} }
} ).
).
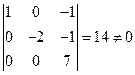 }
} ), называетсяматрица, удовлетворяющая условию:
), называетсяматрица, удовлетворяющая условию: 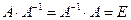 .
. , вычеркнуть i−ю строку и j−ый столбец, на пересечении которых он находится. Поэтому минор Мп−1 матрицы Ап обычно обозначают
, вычеркнуть i−ю строку и j−ый столбец, на пересечении которых он находится. Поэтому минор Мп−1 матрицы Ап обычно обозначают  .
. .
. ………………………………………….(*)
………………………………………….(*) …………….(**)
…………….(**) .
.
 получается det(A) (*), при умножении на любой другой столбец
получается det(A) (*), при умножении на любой другой столбец 
 . {
. { 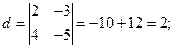
 .(проверка)}
.(проверка)} и левая часть элементарными преобразованиями приводится к единичной. При этом матрица Е преобразуется в обратную {б/д}. Последний пример:
и левая часть элементарными преобразованиями приводится к единичной. При этом матрица Е преобразуется в обратную {б/д}. Последний пример: ;
; 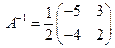 .
. {
{  (св.7,8 §3)
(св.7,8 §3) 
 {Из определения
{Из определения 
 − неизвестная матрица.
− неизвестная матрица. Пользуясь замечанием 1 предыдущего параграфа, имеем:
Пользуясь замечанием 1 предыдущего параграфа, имеем:
 называется системой m
называется системой m . В правой части получается вектор правых частей
. В правой части получается вектор правых частей  (оба вектора – столбцы). Использование этой закономерности позволяет записывать системы в более компактном виде:
(оба вектора – столбцы). Использование этой закономерности позволяет записывать системы в более компактном виде: − матричная форма записи. В случае невырожденной квадратной матрицы решение
− матричная форма записи. В случае невырожденной квадратной матрицы решение
 − решения системы
− решения системы  , т.е. их линейная комбинация тоже решение. Выполнение аксиом − очевидно.}
, т.е. их линейная комбинация тоже решение. Выполнение аксиом − очевидно.} .
.
 , то система имеетединственное решение, которое может быть получено по формулам:
, то система имеетединственное решение, которое может быть получено по формулам: 
 – аналогично. Единственность − от противного.}
– аналогично. Единственность − от противного.} .
. .
.
 в правую часть. Если теперь дать этим неизвестным произвольные фиксированные значения, то по Т. Крамера полученная система будет иметь единственное решение (определитель системы = базисному минору ≠ 0). Это решение (вместе с
в правую часть. Если теперь дать этим неизвестным произвольные фиксированные значения, то по Т. Крамера полученная система будет иметь единственное решение (определитель системы = базисному минору ≠ 0). Это решение (вместе с 

 .
. Последняя формула, вообще говоря, дает общее решение данной системы при произвольных значениях с3 и с4 . Более удобной является векторная форма записи:
Последняя формула, вообще говоря, дает общее решение данной системы при произвольных значениях с3 и с4 . Более удобной является векторная форма записи: .
. зависимыми, а
зависимыми, а 

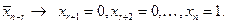
 является частным решением неоднородной системы при с3 = с4 = 0, а векторы
является частным решением неоднородной системы при с3 = с4 = 0, а векторы  линейно независимыми решениями соответствующей однородной системы уравнений. Совокупность линейных комбинаций векторов
линейно независимыми решениями соответствующей однородной системы уравнений. Совокупность линейных комбинаций векторов 
