Метод касательных (метод Ньютона).

Даны функция f(x) и ее первая производная f'(x), непрерывные на a,b. Функция f(x) удовлетворяет условию f(a)*f(b) <= 0. Очередное приближение x_k корня в методе касательных вычисляется по формуле

x_k = x_k-1 - f(x_k-1) / f '(x_k-1),

где x_k-1 - предыдущее приближение корня, f(x_k-1), f'(x_k-1) значения функции и ее первой производной в точке x_k-1.

В качестве начального приближения x₀ принимается одна из границ отрезка, удовлетворяющая условию

f(x₀) * f''(x₀) > 0 (6.2).

Вычисления корня прекращаются при условии, что

abs(x_k - x_k-1) <= Eps и abs(f(x_k)) <= Eps.

Пример вычисления корня уравнения методом касательных в среде Mathcad показан в п.6.5.3. Процесс вычисления корня уравнения методом касательных показан на Рис. 6.1.в.

Рис, 6.1.в. Метод касательных (метод Ньютона)

Метод итераций.

Требуется найти корень уравнения

f(x) = 0 (6.3),

который расположен внутри отрезка a,b. Предполагается, что f(x) непрерывна и имеет единственный корень на a,b.

Исходное уравнение преобразуется к виду

x = Fi(x) (6.4) .

Пусть x₀ некоторая точка из a,b. Подставим x₀ в уравнение (6.4) и вычислим x₁

x₁ = Fi(x₀).

Затем вычислим x₂,x₃, и т.д. На K-м шаге вычислим x_k

x_k= Fi(x_k-1).

Если последовательность x₁,x₂,...,x_k при k ® µ имеет конечный предел x* = lim x_k, то x* является корнем уравнения.

Теорема 3. Если Fi(x) определена и дифференцируема на всей числовой оси и существует положительное число q < 1, такое, что для всех x выполняется неравенство abs(Fi'(x))<q, то уравнение (6.1) имеет единственный корень и процесс итерации сходится к этому корню независимо от выбора числа x₀.

Чтобы уравнение f(x) = 0 удовлетворяло требованию теоремы 3, его следует преобразовать следующим образом.

Умножим левую и правую части уравнения (6.3) на некоторый множитель L. Тогда получим

L * f(x) = 0 (6.5) .

Добавим в левую и правую части уравнения (6.5) по x

x = x + L * f(x).

Введем обозначение Fi(x) = x + L * f(x). Первая производная Fi'(x) будет равна

Fi '(x) = 1 + L * f '(x).

Если множитель L выбрать таким, чтобы

abs(1 + L * f '(x)) < 1 (6.6) ,

то условие теоремы 3 будут выполнены, что гарантирует сходимость итерационного процесса к корню уравнения.

Пример вычисления корня уравнения методом итераций в среде Mathcad показан в п.6.5.4.

Порядок выполнения лабораторной работы.

1. Перед выполнением лабораторной работы студент должен ознакомиться с методическими указаниями.

2. Для заданного преподавателем уравнения студент определяет отрезки, содержащие корень уравнения.

3. В зависимости от выбранного метода решения уравнения необходимо:

· в методе хорд - выбрать начальное приближение корня и неподвижную точку в соответствии с условием (6.1);

· в методе - касательных выбрать начальное приближение в соответствии с условием (6.2);

· в методе итераций - выбрать множитель L в соответствии с условием (6.6).

4. В соответствии с выбранным методом выполнить расчет 3 - 4 шагов приближения корня уравнения.

5. Для выбранного метода решения уравнения необходимо набрать на ЭВМ текст программы.

6. После отладки программы вычисляются приближенные значения корней уравнения с требуемой точностью.

Пример выполнения работы.

Пример решения уравнения методом деления отрезка пополам

Отделение отрезков, содержащих корни.

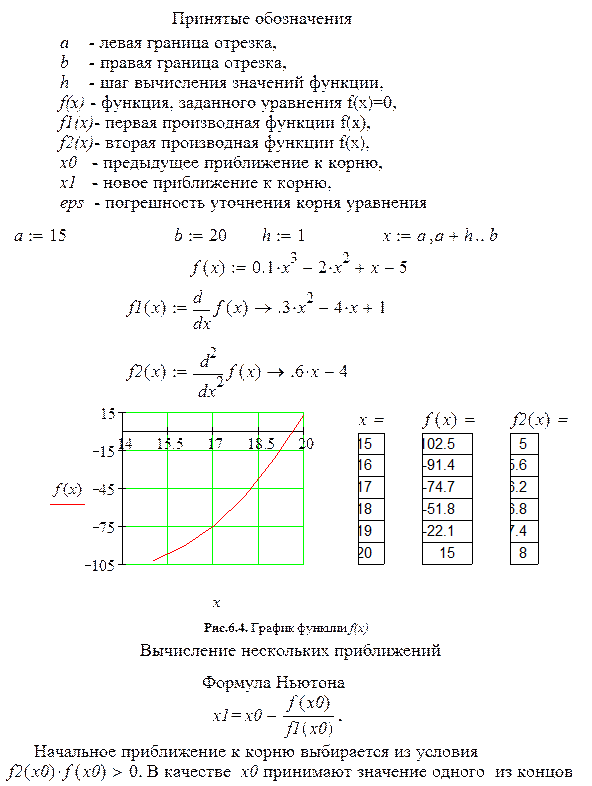
На графике функции f(x) найдем отрезки, удовлетворяющие условиям: f(x) непрерывна, на концах отрезка меняет знак, и монотонна. Данная функция имеет один отрезок, удовлетворяющий указанным выше условиям: a:=15, b:= 20.

Пример решения уравнения методом хорд.

Отделение отрезков, содержащих корни.

В качестве отрезка, содержащем корень уравнения возьмем a=15, b=20, который был получен в п. 6.5.1 графическим методом.

Пример решения уравнения методом касательных

Отделение отрезков, содержащих корни.

В качестве отрезка, содержащем корень уравнения, возьмем a=15, b=20, который был получен в п. 6.5.1 графическим методом.

Пример решения уравнения методом итераций

Отделениеотрезков, содержащих корни.

В качестве отрезка, содержащем корень уравнения, возьмем a=15, b=20, который был получен в п. 6.5.1 графическим методом

.

Содержание отчета

Отчет по лабораторной работе должен содержать :

1. Цель лабораторной работы с указанием уравнения, корень которого должен быть найден.

2. Описание метода решения уравнения

3. Определение отрезков, содержащих корень.

4. Результаты расчетов 3-4 шагов приближения корня.

5. Программу для ЭВМ в среде MathCad, реализующей выбранный метод приближенного вычисления корня.

6. Результаты вычисления корня с заданной точностью

6.7 Контрольные вопросы

1. Какими методами находится отрезок, содержащий корень уравнения ?

2. При каких условиях на отрезке имеется корень уравнения ?

3. Как можно графически представить процесс приближенного вычисления корня уравнения методом половинного деления, методом хорд, методом касательных, методом итераций ?

4. Как выбирается начальное приближение корня уравнения в методе хорд и в методе касательных ?

5. Как преобразовывается исходное уравнение в методе итераций ?

7. Как выбирается корректирующий коэффициент в методе итераций ?

Литература

1. Волков Е.А. Численные методы : Учебное пособие для вузов. - 2-е изд. - М., Наука, 1987.

2. Инженерные расчеты на ЭВМ : Справочное пособие / Под ред. В.А. Троицкого. - Л. Машиностроение, 1979.

3. Копченова Н.В., Марон И.А. Вычислительная математика в примерах и задачах. - М., Наука, 1972.

4. Мак-Кракен Д., Дорн У. Численные методы и программирование на Фортране. - М., Мир, 1969.

5. Троицкий В.А., Иванова И.М. Методы вычислительной математики, ч.1. - Л., изд. ЛПИ им. М.И. Калинина, 1975.

Не нашли, что искали? Воспользуйтесь поиском по сайту: