
|
|
Пусть номер зачетной книжки 1298.Введение В настоящих методических указаниях представлены задачи по темам: линейная алгебра, векторная алгебра, аналитическая геометрия. Методические указания содержат решения типовых примеров, варианты расчетно-графических заданий и список рекомендуемой литературы. Перед выполнением РГР студент должен изучить соответствующие разделы литературы и воспользоваться решениями типовых примеров, содержащихся в настоящих методических указаниях. Номер варианта по каждому заданию кроме второго студент выбирает по формуле где
Пример. Пусть номер зачетной книжки 1235, тогда: номер варианта первого задания: номер варианта второго задания: номер варианта третьего задания: номер варианта четвертого задания: Таким образом, студент, имеющий зачетную книжку № 1235 должен решать задачу №8 в первом задании, №11 – во втором, №14 – в третьем, №17 – в четвертом. Если итоговая цифра по формуле получится число больше 20, то для определения варианта от полученной цифры отнимают 20. Пример. Пусть номер зачетной книжки 1298. Номер варианта второго задания:
Пример 1. Найти уравнение и длину перпендикуляра, опущенного из точки С(1;2) на прямую 3х – 4у + 2 =0. Решение: Через точку С проведем пучок прямых:
Угловой коэффициент «к» найдем из условия перпендикулярности прямых
Подставим найденное значение в уравнение пучка прямых.
Длину этого перпендикуляра найдем по формуле:
В нашем случае это будет: Пример 2. Найти: а) уравнение медианы АЕ; б) прямой, проходящей через точку Е, параллельно стороне АВ в треугольнике с вершинами в точках А(-3;0),В(2;5) и С(4;3). Решение: а) Найдем координаты точки Е – середины отрезка ВС по формулам:
Уравнение медианы найдем, используя уравнение прямой, проходящей через две точки. Подставим в него координаты точек А и Е:
б) Прежде, чем ответить на вопрос задачи, найдем уравнение стороны АВ, как прямой, проходящей через две точки. Затем через точку Е проведем пучок прямых, подчинив его условию параллельности прямых.
Пучок прямых,. проходящих через точку Е: у-4=к (х-3). Условие параллельности прямых
Пример 3. Найти площадь треугольника, образованного двумя векторами
Решение. Площадь треугольника, построенного на векторах
Векторное произведение найдем по формуле:
Найдем модуль полученного вектора, используя формулу:
Тогда искомая площадь будет:
Пример 4. Найти объем пирамиды, построенной на трех некомпланарных векторах:
Решение: Объем пирамиды, построенной на трех некомпланарных векторах как на ребрах, равен
где
Величину
Тогда
Пример 5. Найти каноническое уравнение прямой, проходящей через две точки А(1,2,5) и В(0,1,2). Решение: Подставив координаты точек А и В в уравнение (3.1.13), получим:
Пример 6. Найти уравнение плоскости, проходящей через три точки: А(1, 2, 3); В(1, 1, 0) и С(2, 3, 1). Решение: Используя уравнение , получим:
(х-1)
Пример 7. Через точку А(1, 0, 2) провести прямую, перпендикулярную плоскости Решение. Используем канонические уравнения прямой , подставив координаты точки А, получим:
Проекции направляющего вектора прямой В нашем случае это будет:
Задания. Задание 1. Найти матрицу Х. Сделать проверку. 1.1. x× 1.2 . x× 1.3 . x× 1.4. x× 1.5. x× 1.6. x× 1.7. x* 1.8. x* 1.9. x* 1.10. x* 1.11. x* 1.12. x* 1.13. x* 1.14. x* 1.15. x* 1.16. x* 1.17. x* 1.18. x* 1.19. x* 1.20. x*
Задание 2. Решить систему уравнений:
тремя способами: а) методом Крамера; б) методом Гаусса; в) с помощью обратной матрицы.
Задание 3. Решить задачу. 3.1. Даны вершины тетраэдра А(2;3;1); В(4;1;-2); С(6;3;7); Д(-5;-;8). Найти длину его высоты, опущенной из вершины Д. 3.2. Разложить вектор 3.3. Вычислить объём параллелепипеда, построенного на векторах 3.4. Зная векторы, образующие треугольник 3.5. Даны векторы 3.6. Зная разложение вектора 3.7. Вычислить объём параллелепипеда, построенного на векторах 3.8. Даны векторы 3.9. Зная векторы, совпадающие с двумя сторонами треугольника 3.10. Найти проекцию вектора 3.11. В плоскости Oxy найти вектор 3.12. Даны два вектора 3.13. Разложить вектор 3.14. Вычислить длину диагоналей параллелограмма, построенного на векторах 3.15. Вычислить объём параллелепипеда построенного на векторах: 3.16. Даны разложения векторов, служащих сторонами треугольника, по двум взаимно перпендикулярны ортам: 3.17. Вычислить объём параллелепипеда, построенного на трёх данных векторах 3.18. В треугольнике АВС даны длины его сторон 3.19. Решить задачу
3.20. Вычислить синус угла между диагоналями параллелограмма, построенного на данных векторах
Задание 4 Даны вершины треугольника АВС. а) составить уравнение высоты, проведённой из вершины В, найти её длину. б) составить уравнение медианы, проведённой из вершины А в) составить уравнение биссектрис г) найти для треугольника АВС уравнения вписанной и описанной окружностей д) вычислить площадь треугольника АВС.
4.1 A(3;1) B(0;-2) C(-4;2); 4.2 A(6;4) B(3;1) C(-1;5); 4.3 A(-3;3) B(1;-1) C(4;2); 4.4 A(-1;5) B(-4;2) C(0;-2); 4.5 A(3;9) B(0;6) C(4;2); 4.6 A(7;5) B(4;2) C(0;6); 4.7 A(1;7) B(-2;4) C(2;0); 4.8 A(-6;0) B(-2;-4) C(1;-1); 4.9 A(3;1) B(-1;5) C(2;8); 4.10 A(-1;5) B(3;1) C(6;4); 4.11 A(2;8) B(-1;5) C(3;1); 4.12 A(3;1) B(0;-2) C(-4;2); 4.13 A(-4;2) B(0;-2) C(3;1); 4.14 A(-4;2) B(0;-2) C(3;1); 4.15 A(2;0) B(-2;4) C(1;7); 4.16 A(1;-1) B(-3;3) C(0;6); 4.17 A(-2;4) B(2;0) C(5;3); 4.18 A(-3;3) B(1;-1) C(4;2); 4.19 A(0;-2) B(-4;2) C(-1;5); 4.20. A(0;6) B(-3;3) C(1;-1).
Задание 5 Решить задачу. 5.1. Найти уравнение диагонали параллелограмма, не проходящей через точку пересечения его сторон x+y-11=0 и y+1=0, если известно, что диагонали параллелограмма пересекаются в точке p(-1;0). 5.2. Даны уравнения двух сторон треугольника 4x-5y+9=0 и x+4y-3=0. Найти уравнение третьей стороны, если известно, что медианы этого треугольника пересекаются в точке P(3;1). 5.3. Даны уравнения двух сторон квадрата 5x+12y-10; 5x+12y+29=0. Составить уравнения двух других его сторон при условии, что точка М1(-3;5) лежит на сторон этого квадрата. 5.4. Даны уравнения двух сторон квадрата 5x+12y-10; 5x+12y+29=0. Составить уравнения двух других его сторон при условии, что точка М1(-3;5) лежит на сторон этого квадрата. 5.5 Составить уравнение прямой, проходящей через точку А(-1;2) так, что середина ее отрезка, заключенного между параллельными прямыми x+2y+1=0 и x+2y-3=0, лежит на прямой x-y-6=0. 5.6. Составить уравнение сторон квадрата, если А(-5;5) и В(3;-1) – две его вершины, а Д(2;5) – точка пересечения его высот. 5.7. Составить уравнение сторон треугольника, зная одну из его вершин А(-4;2) и уравнения двух медиан: 3x-2y+2=0; 3x+5y-12=0. 5.8. Вычислить координаты точки пересечения перпендикуляров восстановленных из середин сторон треугольника, вершинами которого служат точки А(2;3); В(0;-3);С(5;-2). 5.9. Вычислить координаты точки пересечения перпендикуляров, восстановленных из середин сторон треугольника, вершинами которого служат точки А(2;3); В(0;-3); С(5;-2). 5.10. Вычислить координаты вершин ромба, если известны уравнения двух его сторон 2x-5y-1=0; 2x-5y-34=0 и уравнение одной из его диагоналей x+3y-6=0. 5.11. Составить уравнение прямой, проходящей через точку А(-1;2) так, что середина ее отрезка, заключенного между параллельными прямыми x+2y-3=0 и x+2y+1=0, лежит на прямой x-y-6=0. 5.12. Даны вершины четырехугольника А(-9;0); В(-3;6); С(3;4); D(6;-3). Найти точку пересечения его диагоналей АС и ВD и вычислить угол между ними. 5.13. В треугольнике АВС известны: сторона АВ: 4x+y-12=0; высота BH: 5x-4y-15=0 и высота AH: 2x+2y-9=0. Написать уравнения двух других сторон и третьей высоты. 5.14. Даны две смежные вершины А(-3;-1) и В(2;2) параллелограмма АВСD и точка Q(3;0) пересечения его диагоналей. Составить уравнения сторон этого параллелограмма. 5.15. Даны вершины треугольника А(1;2) и В(-1;6) и С(5;10). Составить уравнение сторон ромба АМNP вписанного в треугольник так, что вершинами M принадлежит стороне АВ, N – стороне ВС и З – стороне АС. 5.16. Даны стороны четырёхугольника: x-y=2; x+3y=0; x-y-4=0; 3x+y-12=0. Определить его диагонали. 5.17. Найти уравнение прямой, проходящей через точку (2;-1) и составляющей с осью а угол, вдвое больший угла, составляющего с той же осью прямой у= 5.18. Даны вершины четырёхугольника: А(-2;14); В(4;-2); С(6;-2); Д(6;10). Определить точку пересечения его диагоналей АС и ВД. 5.19. Точка А(-4;5) является вершиной квадрата, диагональ которого лежит на стороне7x-y+18=0 Составить уравнения сторон и второй диагонали этого квадрата. 5.20. Дано уравнение одной из сторон квадрата x+3y-7=0 и точка пересечения его диагоналей Р(0;-1). Найти уравнения трёх остальных сторон этого квадрата.
Задание 6 6.1. Составить уравнение линии, каждая точка которой является основанием перпендикуляра, опущенного из начала координат напрямую, проходящую через точку А(2;0). 6.2. Составить уравнение линии, каждая точка которой равноудалена от точки А(2;2) и оси абсцисс. 6.3. Составить уравнение линии, для каждой точки которой расстояние от начала координат и от точки А (0;5) относятся как 3:2. 6.4. Составить уравнение линии, для каждой точки которой расстояние от точки А (1;0) вдвое меньше расстояния от прямой x=4. 6.5. Определить траекторию точки М, которая движется так, что остаётся вдвое дальше от точки F(-8;0), чем от прямой x=-2. 6.6. Дана точка А(2;0). Точка М движется так, что в треугольнике ОМА угол ОМА остаётся прямым. Определить траекторию движения точки М. 6.7. Составить уравнение линии, для каждой точки которой расстояние от точки А(0;1) вдвое меньше расстояния до прямой y=4. 6.8. Определить траекторию точки М, которая при своём движении остаётся втрое ближе к точке А(1;0), чем к прямой X=9. 6.9. Составить уравнение линии, каждая точка которой находится вдвое ближе к точке А(1;0), чем к точке В(-2;0). 6.10. Составить уравнение геометрического места точек, сумма квадратов расстояний которых до точек А(-3;0) и В(3;0) равно 50. 6.11. Найти геометрическое место точек, для которых расстояние до данной точки F(0;-5) равно расстоянию до данной прямой y-5=0. 6.12. Точка М(x, y) движется так, что сумма квадратов расстояний от неё до начала координат и до точки А(-2;0) остаётся равной 4. Определить траекторию движения точки М. 6.13. Составить уравнение линии, каждая точка которой равноудалена от точки А(2;2) и оси абсцисс. 6.14. Составить уравнение линии, каждая точка которой является центром окружности касающейся оси абсцисс и проходящей через точку А(0;3). 6.15. Составить уравнение геометрического места точек, сумма квадратов расстояний которых до точек А(-3;0) и В(3;0) равно 50. 6.16. Составить уравнение линии, каждая точка которой является основанием перпендикуляра, опущенного из начала координат напрямую, проходящую через точку А(2;0). 6.17. Вывести уравнение геометрического места точек, разность расстояний которых до двух данных точек F1 (-5;0) и F1 (5;0), есть величина постоянная, равная 6. 6.18. Составить уравнение траектории движения точки М, которая при движении находятся на одинаковом расстоянии о точки А(3;0) и от прямой х=-3. 6.19. Составить уравнение линии, для каждой точки которой кк расстояние до точки А(4;-1) равно расстоянию до прямой y=1. 6.20. Составить уравнение линии, для каждой таки которой отношение расстояние до начала координат к расстоянию до прямой 3x+16=0 равно 0,6.
Задание 7 Даны координаты вершин пирамиды А1А2А3А4. Требуется найти: а) длину ребра А1А2 б) угол между ребрами А1А2 и А1А4 в) уравнение плоскости А1А2А3 г) площадь грани А1А2А3 д) объем пирамиды е) уравнение прямой А1А4 ж) уравнение высоты, опушенной из вершины А4 на грань А1А2А3 з) угол между ребром А1А4 и гранью А1А2А3
7.1. A1(4;6;3); A2(3;9;8);A3(0;7;1) A4(4;1;5). 7.2. A1(7;9;6); A2(4;5;7);A3(9;4;4) A4(7;5;3). 7.3. A1(4;6;3); A2(3;9;8);A3(0;7;1) A4(4;1;5). 7.4. A1(-1;6;1); A2(-1;1;6);A3(0;4;-1) A4(3;1;4). 7.5. A1(1;2;6); A2(4;2;0);A3(6;1;1) A4(4;6;6). 7.6. A1(7;3;0); A2(2;4;7);A3(6;6;2) A4(5;4;7). 7.7. A1(9;5;5); A2(-3;7;1);A3(5;7;8) A4(6;9;2). 7.8. A1(7;5;3); A2(9;4;4);A3(4;5;7) A4(7;9;6). 7.9. A1(4;1;3); A2(3;2;-1);A3(2;-1;1) A4(5;5;4). 7.10. A1(1;-1;2); A2(3;2;4);A3(-2;0;5) A4(5;2;-3). 7.11. A1(7;5;3); A2(9;4;4);A3(4;5;7) A4(7;9;6). 7.12. A1(4;6;5); A2(6;9;4);A3(2;10;10) A4(7;5;9). 7.13. A1(3;3;9); A2(6;9;1);A3(1;7;3) A4(8;5;8). 7.14. A1(2;2;8); A2(5;8;0);A3(0;6;2) A4(7;0;4). 7.15. A1(4;2;5); A2(0;7;2);A3(0;2;7) A4(1;5;0). 7.16. A1(6;6;2); A2(5;4;7);A3(2;4;7) A4(7;3;0). 7.17. A1(3;5;4); A2(5;8;3);A3(1;9;9) A4(6;4;8). 7.18. A1(0;7;1); A2(4;1;5);A3(4;6;3) A4(3;9;8). 7.19. A1(5;8;2); A2(3;5;10);A3(5;5;4) A4(3;8;4). 7.20. A1(4;1;3); A2(3;2;-1);A3(2;-1;1) A4(5;5;4).
Задание 8 Решить задачу 8.1. Написать уравнение плоскости, которая проходит через точку (3;1;-2) и через прямую 8.2. Составить уравнение плоскости, проходящей через точку P(4;-3;1) и параллельной прямой: 8.3. Провести плоскость через перпендикуляры, опущенные из точки (-3;2;5) на плоскости 4x+y-3z+13=0 и x-2y+z-11=0. 8.4. Написать уравнение перпендикуляра опущенного из точки (2;3;1) на прямую 8.5. Составить уравнение прямой, проходящей через точки пересечения плоскости 2x+y-3z+1=0 c прямыми 8.6. Найти расстояние точки М(7;9;7) от прямой 8.7. Составить уравнения прямой, проходящей через точку М0(2;-3;-5) перпендикулярно к плоскости 6x-3y-5z+2=0. 8.8. На прямой 8.9. На прямой 8.10. Даны вершины треугольника А(4;1;-2); В(2;0;0) и С(-2;3;-5). Составить уравнения биссектрис угла А треугольника. 8.11. Проверить, что прямые 8.12. Написать уравнение плоскости, проектирующей прямую 8.13. Написать уравнение прямой, проходящей через начало координат и составляющей равные углы с плоскостями 4y=3x; y=0 и z=0. Найти эти углы. 8.14. На прямой 8.15. Написать уравнение плоскости, проектирующей прямую 8.16. Найти точку симметричную точке Р(4;3;10) относительно прямой 8.17. Даны плоскость x+y-z=0 и прямая, проходящая через точки А(0;0;4) и В(2;2;0). Найти точку пересечения прямой с плоскостью и угол между ними. 8.18. Составить уравнение плоскости, проходящей через точку М0 (1;-1;-1) перпендикулярно к прямой 8.19. Составить канонические уравнения прямой, проходящей через точку М0 (2;-4;-1) и середину отрезка прямой 8.20. Проверить, что прямые
Библиографический список 1. Шипачев В.С, Высшая математика: Учеб./под ред. А.Н. Тихонова. – 2-е изд. стереотип. – М.: Высш. шк., 1990. – 479 с. 2. Письменный Д.Т. Конспект лекций по высшей математике. I, IIч.. –М.:Рольф, 2002. – 288с.
3. Зайцев И.А. Высшая математика: Учеб. – М.: Высш. шк., 1991. – 400с.
4. Данко П.Е. и др. Высшая математика в упражнениях и задачах: В 2ч. – М.: Высш. шк. т.1. – 1999. – 304 с.
4. Шипачев В.С. Задачник по высшей математике: Учеб. пособие. – 2-е изд., испр. – М.: Высш. шк., 2000. – 304 с.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ,
, - номер варианта,
- номер варианта, -номер задания,
-номер задания, -предпоследняя цифра зачетной книжки студента,
-предпоследняя цифра зачетной книжки студента, -последняя цифра зачетной книжки студента.
-последняя цифра зачетной книжки студента. =
=  ;
; ;
; ;
; .
. . Промежуток 26-20=6. Таким образом, во втором задании студент решает задачу вариант №6.
. Промежуток 26-20=6. Таким образом, во втором задании студент решает задачу вариант №6.
 , для чего прежде найдем угловой коэффициент заданной прямой.
, для чего прежде найдем угловой коэффициент заданной прямой. тогда
тогда  .
. уравнение перпендикуляра.
уравнение перпендикуляра. где
где - координаты точки С.
- координаты точки С.
 Е(3;4).
Е(3;4). .
. ;
; 
 .
. . Подставим это значение «к» в уравнение пучка, у-4=х-3, или у=х+1.
. Подставим это значение «к» в уравнение пучка, у-4=х-3, или у=х+1. и
и , выходящими из одной точки.
, выходящими из одной точки. и
и  , равна половине площади параллелограмма, построенного на этих же векторах как на сторонах, т.е. равна
, равна половине площади параллелограмма, построенного на этих же векторах как на сторонах, т.е. равна  модуля векторного произведения векторов
модуля векторного произведения векторов  .
.

 (кв.ед.)
(кв.ед.) .
. , где
, где  ,
, -смешанное произведение векторов.
-смешанное произведение векторов.
 (куб.ед.).
(куб.ед.).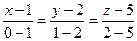 ;
; 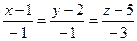 ;
;  .
.

 ,
,



 .
. найдем из условия перпендикулярности прямой и плоскости .
найдем из условия перпендикулярности прямой и плоскости . , тогда будем иметь:
, тогда будем иметь:  .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. две последние цифры зачетки.
две последние цифры зачетки. .
. .
. =
=  по взаимно перпендикулярным ортам
по взаимно перпендикулярным ортам  , образующим правую тройку.
, образующим правую тройку. , где
, где  - взаимно перпендикулярные орты.
- взаимно перпендикулярные орты. ;
;  ;
;  , где
, где  и
и  - взаимно перпендикулярные орты, определить углы этого треугольника.
- взаимно перпендикулярные орты, определить углы этого треугольника.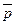 и
и  , удовлетворяющими условиям:
, удовлетворяющими условиям: 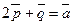 ;
;  ;
; по трём перпендикулярным ортам, вычислить длину вектора
по трём перпендикулярным ортам, вычислить длину вектора  ,
,  и
и 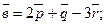
 где
где  - взаимно перпендикулярные орты.
- взаимно перпендикулярные орты. , если известно, что он компланарен векторам
, если известно, что он компланарен векторам  .
. и
и  , вычислить углы этого треугольника.
, вычислить углы этого треугольника. на ось, имеющую направление вектора
на ось, имеющую направление вектора  , где
, где  - взаимно перпендикулярные орты. Вычислить углы между осью проекций и единичными векторами
- взаимно перпендикулярные орты. Вычислить углы между осью проекций и единичными векторами 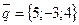 и имеющий одинаковую с ним длину.
и имеющий одинаковую с ним длину. и
и  . Найти единичный вектор, лежащий в плоскости векторов
. Найти единичный вектор, лежащий в плоскости векторов  и
и  , если известно, что
, если известно, что  =2
=2  ,
,  =3 и угол между
=3 и угол между  = π/4.
= π/4. Где p, q, взаимно перпендикулярные орты.
Где p, q, взаимно перпендикулярные орты. ;
;  . Вычислить длину медианы АМ и высоту АД треугольника АВС.
. Вычислить длину медианы АМ и высоту АД треугольника АВС. ={-4;0;3};
={-4;0;3};  ={1;5;-1} и исследовать, образуют ли векторы левую или правую тройку.
={1;5;-1} и исследовать, образуют ли векторы левую или правую тройку. =5;
=5;  =6;
=6;  =7. Найти скалярное произведение векторов
=7. Найти скалярное произведение векторов  ;
;  ;
;  ;
;  . Доказать, что АВСD – параллелограмма.
. Доказать, что АВСD – параллелограмма. и
и  , где
, где  - взаимно перпендикулярные орты.
- взаимно перпендикулярные орты. .
. .
. и
и  .
. .
.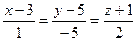 и
и  .
.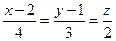 .
.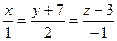 найти точку, ближайшую к точке (3;2;6).
найти точку, ближайшую к точке (3;2;6). найти точку, одинаково удаленную от двух данных точек А(3;11;4) и В(-5;-13;-2).
найти точку, одинаково удаленную от двух данных точек А(3;11;4) и В(-5;-13;-2). и
и  пересекаются и написать уравнение плоскости, через них проходящей.
пересекаются и написать уравнение плоскости, через них проходящей. на плоскость XOY.
на плоскость XOY.
 .
. .
. , заключённого между плоскостями 5x+3y-4z+11=0; 5x+3y+4z-41=0.
, заключённого между плоскостями 5x+3y-4z+11=0; 5x+3y+4z-41=0.
 и
и  пересекаются и написать уравнение плоскости, через них проходящей.
пересекаются и написать уравнение плоскости, через них проходящей.