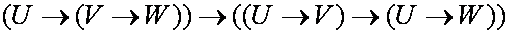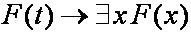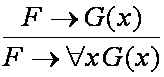|
|
Отношение и предикат Кванторы. Язык логики предикатов. Аксиомы. Правила вывода. Свойства исчисления предикатов.12
В ряде случаев высказывания касаются свойств объектов или отношений между ними, при этом требуется иметь возможность утверждать, что любые или какие-то объекты обладают определенными свойствами или находятся в некоторых отношениях. Одноместные (унарные) отношения называются признаками или свойствами. Предикат является индикатором отношения, предикат может принимать значения истина или ложь в зависимости от того имеет место или нет данное отношение. Например: Отношение – больше - для которого используется знак >. Выражения 2>3, 22>3 имеют ложное или истинное значение. Предикат x>5 (x>y) – функция, которая будет принимать значения истина или ложь в зависимости от значений входящих в нее переменных. n – местным предикатом P(x1,x2,…,xn) называется функция P: Mn →B , где M - произвольное множество, а B={0,1}. Кванторы. Пусть P(x1,x2,…,xn) - предикат. Переменные x1,x2,…,xn называются свободными. Переход от данного выражения к Выражение, не имеющее свободных переменных называется высказыванием. Выражение, на которое навешан квантор, называется областью действия квантора. Значение истинности выражения зависит от значения свободных переменных и не зависит от значений связанных переменных, поэтому переименование связанной переменной в области действия квантора не изменяет значения истинности всего выражения. Например: Предикат Мать(x,y) означает, что x является матерью для y, тогда Язык логики предикатов. Собака – друг человека. Мартик – собака. Татьяна – человек. Следовательно, Мартик - друг Татьяны. Верно ли это логическое заключение? R(x,y) – предикат, обозначающий, что x является другом y. R1(x) – свойство «субъект с именем x является собакой» R2(x) – свойство « x - имя человека». Первое утверждение можем записать так: Второе утверждение - R1(M), третье – R2(Т). Логическое заключение будет иметь вид: R(М,Т). Таким образом, требуется доказать (или опровергнуть), что: { или, что то же самое, доказать или опровергнуть, что ( будет истинной формулой в данной интерпретации. Не трудно доказать, что это так и будет, причем вне зависимости от того, какой смысл будет вкладываться в R, R1, R2, x, y, М,Т то есть независимо от интерпретации и в любой интерпретации. Язык исчисления высказываний является частным случаем языка исчисления предикатов, значит пропозициональные формулы (высказывания) являются формулами языка исчисления предикатов. Символы языка: - логические связки: - кванторы:{ - предметные переменные; - предметные константы; - функциональные символы: {f,f1,g,…,F,φ,…}; - математические функции; - предикатные символы:{P,P1,…Q,Q1,…R,…}; Термы – это или предметные константы, или предметные переменные, или выражения вида: где f(n)- n – местный функциональный символ. t1,…,tn – термы. n>0. (при n=0 терм называют предметной или функциональной константой). Атомарные (элементарные) формулы – выражения вида: Формулами исчисления предикатов являются либо атомарные формулы, либо выражения вида: где Литералами называются формулы вида Любое вхождение предметной переменной Формула, к которой применяется квантор по данной переменной, называется областью действия этого квантора. Предметная переменная называется свободной, если она не находится в области действия какого-либо квантора. Формула, не содержащая свободных переменных, называется замкнутой, и представляет собой высказывание, не зависящее от предметных переменных. Аксиомы исчисления предикатов: - аксиомы исчисления высказываний: o o o - собственные аксиомы исчисления предикатов: o o в этих аксиомах t свободен для x в формуле F, F(t) получена из F(x) заменой всех свободных вхождений x на t. Правила вывода: В этих аксиомах предполагается, что G(x) содержит свободные вхождения x, а F их не содержит, в противном случае можно получить неправильные выводы. - Правило заключения (modus ponens) то же, что и в исчислении высказываний: - Правило обобщения или правило введения квантора всеобщности: - Правило введения квантора существования: . Логический вывод в исчислении предикатов. С точки зрения программирования на Прологе формула, которую нужно доказать в прикладном исчислении предикатов, должна логически следовать из множества формул, составляющих программу. В противном случае программа или будет работать неправильно, или правильно с точки зрения логики, но не будет приводить к требуемому результату. - суть первого шага метода резолюций приведена в п.4. и состоит в получении формулы, противоречивость которой необходимо доказать; - приведение ее к предваренной форме (исключить связки эквивалентности и импликации, уменьшить область действия отрицания, переименовать, если это необходимо связанные переменные, удалить кванторы, если это возможно или перенести их в начало формулы); - приведение к клаузальной форме (которую можно записать в виде множества дизъюнктов); - проведение опровержения на основе правила резолюций

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 или
или 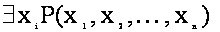 называется навешиванием квантора на переменную
называется навешиванием квантора на переменную  или связыванием переменной
или связыванием переменной 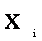 .
. Мать(x,y) означает, что у каждого человека есть мать, - истинное утверждение.
Мать(x,y) означает, что у каждого человека есть мать, - истинное утверждение.  Мать(x,y) означает, что существует мать всех людей, что является другим утверждением, истинность которого зависит от множества значений, которые могут принимать y: если это множество братьев и сестер, то оно истинно, а в противном случае оно ложно. Таким образом, перестановка кванторов всеобщности и существования может изменить смысл и значение выражения.
Мать(x,y) означает, что существует мать всех людей, что является другим утверждением, истинность которого зависит от множества значений, которые могут принимать y: если это множество братьев и сестер, то оно истинно, а в противном случае оно ложно. Таким образом, перестановка кванторов всеобщности и существования может изменить смысл и значение выражения. (R1(x) &R2(y)→ R(x,y)).
(R1(x) &R2(y)→ R(x,y)).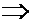 R(М,Т)
R(М,Т) ;
; };
};
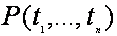 , где
, где  - предикатный символ, ti– термы, n≥0 (при n=0 атомарная формула совпадает с пропозициональной переменной.
- предикатный символ, ti– термы, n≥0 (при n=0 атомарная формула совпадает с пропозициональной переменной.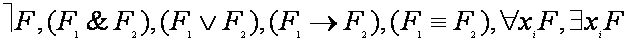
 - формулы,
- формулы,  - предметная переменная.
- предметная переменная.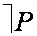 , где
, где  или
или  называется связанным, а предметная переменная – связанной.
называется связанным, а предметная переменная – связанной.