
|
|
ФОРМЫ РАЗВИТИЯ ЗНАНИЯ: ПРОБЛЕМА. ГИПОТЕЗА. ТЕОРИЯ.1. Проблема (вопрос). Виды вопросов и ответов. 2. Понятие гипотезы, ее виды. 3. Построение гипотезы и этапы ее развития. Способы подтверждения гипотез. 4. Теория как наиболее сложная форма научного мышления. Литература 1. Ивлев Ю.В. Теория и практика аргументации: Учеб. для вузов /Ю.В.Ивлев – М., Проспект, 2011. 2. Логика / Мигунов А.И., Микиртумов И.Б., Федоров Б.И. и др. – М., Проспект, 2010 - 700с. 3. Гетманова А.Д. Логика: Углубленный курс. Учебное пособие/ А. Д. Гетманова – М., Кнорус, 2008, - 192 с. 4. Хоменко И. В. Логика. Теория и практика аргументации . М.: Юрайт, 2010. 320 с. ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА 5.Андреева И.Д. Научная теория как форма организации научного знания. - М., 1979. 6.Иоселиани А.Д. Место и роль гипотезы в становлении современного научного знания. - М., Финансовая академия, 1999 . В данной теме студент должен понимать следующие вопросы: 1) Проблема. Неразвитая и развитая проблема. 2) Понятие гипотезы. Гипотеза как форма развития знаний. Логическая природа гипотез. 2.1). Виды гипотез: общие и частные. Понятие рабочей гипотезы. Условия отбора предпочтительных гипотез. 2.2).Построение гипотезы и этапы ее развития. 2.3).Роль умозаключения и опытных данных при построении гипотез. 2.4). Способы подтверждения гипотез. Основной способ подтверждения гипотез: выведение следствий и их верификация. 3) Теория как высшая и наиболее сложная форма научного мышления: 3.1). Исходные основания. 3.2). Объект теории. 3.3). Система законов и утверждений 4) Основные функции теории: а) описание, б) объяснение, в) предсказание.
X. Образцы решения логических задач Теория логики - это лишь исходное условие и средство, помогающее привить навыки правильного рассуждения, применять на практике логические законы, приемы и операции. Важную роль в формировании этих навыков играют систематические упражнения в решении логических задач. Предлагаемые образцы решения задач ориентированы на использование лишь элементарных логических актов, а потому умение их выполнять может считаться базовым для оценки развитости правильного мышления. Поскольку пособие предназначено для изучения курса логики в рамках подготовки специалистов различных областей, предлагаемые образцы решения задач могут служить основой для выполнения контрольных работ студентов всех форм обучения Государственной полярной академии. Образцы решения задач подобраны на основные темы, предусмотренные программой курса. Приступать к анализу образцов решения задач и их записей следует лишь после того, как изучен теоретический материал, проанализированы таблицы и схемы по каждой из тем.
ПРЕДМЕТ ЛОГИКИ. ОСНОВНЫЕ ПОНЯТИЯ И СТРУКТУРА ЛОГИКИ Предмет и основные понятия логики 1. Установите, какие из следующих выражений являются понятиями, суждениями и умозаключениями. А) Самая удаленная точка Вселенной Б) Великий русский писатель Л.Н. Толстой В) Сфинкс Г) Государство Д) Приведения не существуют Е) 510 больше 333 Ж) На Марсе есть жизнь 3) Все киты млекопитающиеся И) Все металлы электропроводны. —> Ни один не электропроводник не является металлом. К) Некоторые музыканты играют на пианино. —> Все пианисты являются музыкантами.
Решение. Первые четыре выражения - понятия, следующие четыре – суждения, последние два – умозаключения. 2. Установите, какие из следующих высказывании имеют одинаковую логическую форму. А) Всякое дерево есть растение. Г) Некоторые лекции являются увлекательными. Высказывания А) и Б) имеют одинаковую логическую форму: « Все S есть P» , а В) и Г) : «Некоторые S есть P». 3. Определите, есть ли противоречие в следующих утверждениях или в них нарушен принцип тождества. А) Я в Бога не верю, однако он есть. Решение. В этом утверждении выражения «не верю» и «однако он есть» не противоречат друг другу, т.к. первое и второе выражения несут разную смысловую нагрузку. Поэтому нарушен здесь скорее принцип тождества. Б) Ноздрев был в некотором отношении исторический человек. Ни на одном собрании, где он был, не обходилось без истории (II.В. Гоголь). Решение. В этом выражении нарушен закон тождества, поскольку употребление омонимов ведет к двусмысленности. В) Если трава зеленая, то она зеленая. Решение. В этом утверждении совершенно ясно выражена формула закона тождества (А → А, если А истинно, то оно истинно). Поэтому здесь закон тождества не нарушен. 4. Определите, нарушен ли принцип непротиворечивости мышления в следующих утверждениях. А) Я знаю, что я ничего не знаю (Сократ). Решение. В этом утверждении Сократ противоречит сам себе, если он знает, что он ничего не знает, то он и этого не знает. Поэтому данное утверждение скрывает в себе противоречие. Б) Все грибы являются растениями или животными (А), и тем не менее они не являются ни растениями, ни животными (В). Решение. Если две части этого высказывания обозначить как А и В, тогда станет очевидно, что в этом высказывании заключено отношение противоположности, т.к. в первой части (А) делается утверждение относительно грибов, во второй части (В) - отрицание. В) Неверно, что птицы летают, и что они не летают. Решение. В этом утверждении совершенно ясно выражена формула закона непротиворечия ( (А & А), неверно что истинно А и не-А). Поэтому здесь закон непротиворечия не нарушен. 5. В каких из следующих высказываний нарушен принцип исключенного третьего. А) Все грибы являются съедобными (А) или же ни один гриб не является съедобным (В). Решение. Если две части этого высказывания обозначить как А и В, тогда станет очевидно, что принцип исключенного третьего нарушен, поскольку согласно этому принципу, одно из них (либо А, либо В) должно быть истинно. В данном высказывании две части не могут быть истинными, но могут быть обе ложными. Поэтому здесь действует лишь закон непротиворечия и не действует закон исключенного третьего. Б) Про данный гриб нельзя сказать, что он является съедобным (А), так же как и неверно было бы говорить, что он не является съедобным (К). Решение. В данном высказывании две части (А и В) не отрицают одна другую: то, что данный гриб несъедобен, является не отрицанием того, что он съедобен, а более сильным высказыванием, при этом может оказаться, что обе части ложны, т.е. данный гриб может быть определен как условно съедобным. Следовательно, в приведенном высказывании принцип исключенного третьего не нарушен. В) Аристотель умер в 322 году до н.э. или он не умер в этом году. Решение. В этом высказывании совершенно ясно выражена формула закона исключенного третьего (А v а, истинно либо А, либо не-А). 6. Является ли последующая мысль достаточным основанием для первой? Студент Иванов вряд ли решит задачи по логике. Студент Иванов не может решить задачи по логике. Студент Иванов, как правило, не умеет решать задач по логике. Решение. Третье высказывание является достаточным основанием для первого, в котором выражается сомнение по поводу способностей в решении задач по логике, но является достаточным основанием для второго, потому что неумение решать задачи в большинстве случаев оставляет возможность для исключения из этого правила, т.е. нет достаточных оснований считать, что студент Иванов не решит какую-то конкретную задачу. Глава 2. Логический анализ языка 1. Какие из следующих выражений являются знаками, а какие не являются? Б) NaOH + 17. Решение. Первое выражение является знаком, поскольку оно выражает свойство числа; второе – нет, ибо оно не имеет смысла и значения. Однако при рассмотрении составляющих частей второго выражения часть независимо друг от друга имеет и смысл и значение. 2. Укажите предметное значение следующих выражений. А) Сумма 5+5. Б) «Жизнь за царя». В) Щука - рыба. Решение. Значением первого выражения является число 10; значением второго - название оперы; значением третьего - истина. 3. Укажите, какие высказывания истинны, а какие ложны, и почему? А) Москва - столица России. Б) «Москва» - имя того города, который можно обозначить также словосочетанием «столица России». В) Москва - название города. Решение. Третье утверждение является ложным, т.к. значением выражения слева от тире является «город», тогда как значением выражения справа от тире является «название города». Истинным будет выражение: «Москва» - есть имя, обозначающее город». Первое высказывание также является истинным. 4. Определите дескриптивные и логические термины в высказывании: «Все грибы являются растениями или животными». Решение. В данном высказывании дескриптивными терминами являются: «грибы», «растения», «животные», а логическими терминами: «все», «или».
5.Определите, к каким семантическим категориям относятся следующие выражения. А) Листва, упавшая на землю. Б) Семена упали на землю. К) Когда будут собраны семена? Г) Отец Перикла Решение. А) Листва, упавшая на землю - дескриптивный термин, имя предмета. Б) Семена упали на землю - суждение, выраженное в форме повествовательного предложения. В) Когда будут собраны семена? - вопросительное предложение, не содержащее суждения. Г) Отец Перикла— дескриптивный термин, имя предмета. 6. Укажите, какие функции могут быть представлены термином «сестра» (общая форма записи, местность вид функции, область определения (области возможных аргументов), значения). Решение. Термином «сестра» могут быть представлены две функции: А) Сестра Х - одноместная предметно-предметная функция, область определения которой – множество людей, а область значения - множество женщин. Б) Х сестра У- двухместная предметно-пропозициональная функция, области возможных аргументов которой множество женщин и множество людей, область определения -множество упорядоченных пар женщин, человек, а область значения - множество, состоящее из двух абстрактных объектов - истина, ложь. 7. Определите составляющие термины следующего выражения: «Число является простым тогда и только тогда, когда оно делится на себя, на единицу и не делится ни на какие другие числа». Решение. В данное выражение входят термины: «число» - общее имя, «является простым» - одноместный предикатор, «тогда, и только тогда, когда» - логическая связка (эквиваленция), «оно (число)» - общее имя, «делится на» - двухместный предикатор, «себя (число)» - общее имя, «единица» - единичное имя, «и» - логическая Глава 3. Основные понятия и направления символической (математической) логики 1. Запишите на языке логики высказывания следующее высказывание: «Если бы Иван IV был зол по природе и не заботился об интересах государства, то он не отменил бы опричнины». Решение. В этом сложном высказывании следует определить простые высказывания и обозначить их определенными символами: р - простое высказывание «Иван IV был зол по природе»; q - простое высказывание «не заботился об интересах государства»; r - простое высказывание «он не отменил бы опричнины»; ^ - конъюнкция соответствует союзу «или»; → - импликация соответствует союзу «если..., то». Тогда логическая форма данного сложного высказывания может быть записана в виде формулы: (р ^ q) → r 2. Переведите следующие высказывания естественного языка на язык логики предикатов: А) Наталья - девушка. Решение. Формула Р(а), где предметная константа а соответствует имени «Наталья», а одноместная предикаторная константа Р - знаку свойства - «девушка». Б) Анастасия любит Андрея. Решение. Формула R(а, Ь), где R соответствует двухместному предикатору «любит», а а и b - именам Анастасия», «Андрей».
Г) Всякая девушка красива.
Е) Ни одна девушка не красива.
Ж) Всякий ученик любит какую-нибудь одноклассницу.
Буквальный смысл – этой записи - «Для всякого человека х верно, что если он ученик, то существует человек у, такой, что он одноклассница и х любит у». 3) Некоторые ученики любят всякую одноклассницу.
И) Некоторые ученики не любят ни одной одноклассницы.
РАЗДЕЛ II Глава 4. Общая характеристика понятия 1. Раскройте содержание понятия «коллега» и запишите его логическую форму на языке логики предикатов. Решение. Содержание: человек (родовой признак), который служит или работает вместе с кем-нибудь (видовое отличие). Логическая формула понятия:
2. Сравните содержание и объем понятия «наказание» и «ограничение свободы». Решение. Понятие «ограничение свободы» (В) видовое по отношению к
3. Дайте полную логическую характеристику (определите вид)понятиям«юрист» и « человек , не знающий страха». Решение. «Юрист» - понятие непустое, общее, нерегистрирующее, конкретное, положительное, безотносительное. « Человек, не знающий страха» - понятие непустое, общее, нерегистрирующее, абстрактное, отрицательное, относительное.
Глава 5. Отношения между понятиями 1. Подберите понятия, находящиеся в отношении соподчинения к понятию«религия». Решение. Соподчиненными понятию «религия» (А)
2. Определите вид отношения между понятиями «каменный дом», «недостроенный дом», «дом», «строение», «гараж». Решение. Понятие «каменный дом» (А) и понятие «недостроенный дом» (В) находятся в отношении пересечения. Понятия (А) и (В) находятся в подчинении понятию «дом» (С). Понятие «дом» (С) и понятие «гараж» (Д) являются несовместимыми понятиями, находящимися в соподчинении понятию «строение» (Е).
Глава 6. Логические операции с понятиями 1. Проверьте правильность обобщения: «равносторонний треугольник - равноугольный треугольник - треугольник». Решение. Обобщение неверное, т.к. первое понятие не является видовым по отношению ко второму, а равнозначно с ним. Нарушено требование к обобщению. 2. Ограничьте понятие: «периодическое издание». Решение. Ограничением понятия «периодическое издание» является понятие «газета». 3. Определите, в каком примере произведено таксономическое деление понятия (отношение «род- вид»), а в каком мереологическое деление (отношение «часть-целое»); в каком примере высказывание является операцией определения понятия. Сделайте полный разбор определения или деления. В примере деления установите: вид деления, делимое понятие, члены деления, основание деления. В примере определения укажите вид определения, произведите анализ определения через род и видовое отличие. Определите, является ли операция (определения или деления) правильной, если нет, то укажите какие правила нарушены. А) «Приговоры бывают обвинительными, оправдательными и справедливыми». Решение. В данном высказывании заключено таксономическое деление понятия, т.к. раскрывается объем понятия «приговоры». Вид деления: по видоизменению признака, делимое понятие «приговоры»,члены деления : «обвинительные, оправдательные, справедливые». Деление неправильное, т.к. нарушены правила деления. Деление понятия «приговоры» произведено не по одному основанию. Б) «По устройству часы делятся на механизм, циферблат, корпус, стекло, заднюю крышку, браслет, замок на браслете». Решение. В данном высказывании заключено мереологическое деление понятия «часы». Деление является неправильным. Здесь часть членов деления («механизм», «циферблат», «корпус», «стекло», «задняя крышка выделены по одному основанию (устройства часов), а часть («браслет», «замок на браслете») - по другому основанию (аксессуаров часов). В) «Понятие - это форма мышления, отражающая предметы в их существенных признаках». Решение. Это высказывание является определением, т.к в нем раскрывается содержание понятия. Определение явное, реальное через род и видовое отличие. Определяемое понятие (А) - «понятие», определяющее понятие (В) - «форма мышления, отражающая предметы в их существенных признаках», где «форма мышления род, «отражающая предметы в их существенных признаках» - видовое отличие. Определение является правильным, т.к. в нем не нарушены правила определения. Простые суждения 1. Укажите субъект и предикат в следующих суждениях и определите, являются они атрибутивными или с отношениями. А) Спаниель – собака. Решение. «Спаниель» - субъект, «собака» - предикат (признак - свойство), ассерторическое простое атрибутивное суждение. Б) Роза имеет приятный запах. Решение. «Роза» - субъект, «приятный – запах» - предикат (признак - свойство), ассерторическое простое атрибутивное общеутвердительное суждение. В) Растения при дыхании выделяют кислород. Решение. «Растение» - субъект, «выделяют при дыхании кислород» - предикат (признак - свойство), ассерторическое простое общеутвердительное атрибутивное суждение. Г) Некоторые люди не знают ни одного закона физики. Решение. Субъект этого суждения - пара понятий («люди», «законы физики»), предикат - двухместное отношение «знают» и перед ним - отрицание, ассерторическое простое суждение с отношениями, по количеству – общее - общее. Д) Роман дарит Ольге цветы. Решение. Субъект этого суждения - тройка понятий («Роман», «Ольга», «цветы»), предикат – трехместное отношение «дарит», ассерторическое простое суждение с отношениями, по количеству – единично-единичное-общее. Е) Осенние яблоки были не хуже летних. Решение. «Осенние яблоки» - субъект, «были не хуже летних» - предикат (признак - свойство), ассерторическое общеутвердительное атрибутивное суждение. Ж) Осенние яблоки были не хуже, чем летние. Решение. Субъект этого суждения - пара понятии («осенние яблоки», «летние яблоки»), предикат - двухместное отношение «были не хуже, чем», ассерторическое простое суждение с отношениями, по количеству – частное-частное. 3) Права авторов (S1), рационализаторов (S2) и изобретателей (S3) охраняются государством (Р). Решение. Данное суждение можно рассматривать как сложное, состоящее из трех простых или как простое со сложным субъектом. Логическая форма S (S1, S2, S3) есть Р. И) Никто (S) не может быть подвергнут произвольному аресту (P1), задержанию (Р2) или изгнанию (Рз). Решение. Данное суждение можно рассматривать как сложное, состоящее из трех простых или как простое со сложным предикатом. Логическая форма S есть Р (Р1,P2,Р3). 2. Определите количество и качество следующих суждений с отношениями. А) Игорь старше Павла. Решение. Суждение утвердительное, единично-единичное. Б) Каждый студент 501 группы знает каждого преподавателя кафедры философии. Решение. Суждение утвердительное, обще-общее. В) Некоторые студенты 501 группы знают некоторых преподавателей кафедры логики. Решение. Суждение утвердительное, частно-частное. Г) Все студенты 751 группы изучают логику. Решение. Суждение утвердительное, обще-единичное. Д) Некоторые студенты 751 группы изучают логику. Решение. Суждение утвердительное, частно-единичное. 3. Определите вид суждений и укажите распределенность терминов в них. А) Некоторые студенты - спортсмены. Решение. Субъект - «студенты», предикат - «спортсмены», квантор существования - «некоторые». Б) Ни один тигр не есть травоядное животное. Решение. Субъект - «тигр», предикат - «травоядное животное», квантор общности - «ни один». 4. Определите вид суждения. Найдите квантор, субъект, предикат, определите количество и качество А) Все квадраты - равносторонние прямоугольники.
Квантор общности - «все». Субъект суждения - «квадрат» (S). Предикат суждения - «равносторонние прямоугольники» (Р). По количеству данное суждение - общее. S, P По качеству - утвердительное. Схема суждения: «Все S есть Р». Данное суждение - общеутверднтельное (А). Схема отношения между терминами: S - распределен P - распределен Б) Некоторые виды уголовного наказания предусматривают лишение свободы. Квантор существования - «некоторые». Субъект суждения - «виды уголовного наказания» (S) Предикат суждения - «предусматривают лишение свободы» (Р). По количеству данное суждение - частное. По качеству - утвердительное. Схема суждения: Некоторые S есть Р. Данное суждение - частноутвердительное (1). Схема отношения между терминами:
S-нераспределен
Р - нераспределен Глава 9. Сложные суждения 1. Составьте символическую запись следующего сложного суждения на языке логики высказываний: Решение. Приводим данное сложное суждение в явную логическую форму: «Если служащий нарушил Где P - служащий нарушил дисциплину Q - администрация предприятия обязана взять у него устные объяснения Где P, Q, R - простые суждения, соединенные между собой логическими союзами. В символической записи: P → (Q V R) 2. Запишите логическую форму следующего сложного суждения на языке логики высказываний, «Если человек читал книгу, то он знает ее содержание или основную идею». Решение. Данное суждение состоит из трех простых: «человек читал книгу» (P), человек знает ее содержание» (Q), «человек знает ее идею» (R). Логическая форма: ( P → (Q V R)). Истинностная таблица имеет вид
Формула выполнимая, но не тождественно-истинная. 3. Определите, какие из следующих формул являются тождественно-истинными, какие тождественно-ложными и какие собственно выполнимыми: А) (р→q) v (q → р) Решение. Истинностная таблица имеет вид:
Формула является тождественно истинной. Б) ( P ^ Q) = ( P V Q) Решение. Истинностная таблица имеет вид:
Формула является тождественно ложной. Глава 10. Отрицание суждений Произведите отрицания следующих суждений. А) «Существуют жильцы, которые не знают своих соседей». Решение. Это высказывание является ассерторическим простым частноотрицательным суждением. При отрицании частно-частноотрицательного суждения получается обще-общеутвердительное суждение («Некоторые S не есть Р» —> «Все S есть P»). В качестве результата получается суждение: «Каждый жилец знает всех своих соседей». Б) «Если у меня будет свободное время (P), то я прочту интересную книгу (Q) или пойду в театр (R). Решение. Это высказывание является сложным суждением, его логическая форма: Р → (Q V R) Противоречащее суждение будет иметь следующую логическую форму: (Р → (Q V R)) = (Р V(Q V R ) = Р ^ (Q ^ R) , а читаться оно будет так: «У меня будет свободное время, но я не прочту интересную книгу и не пойду в театр». Глава 11. Отношения между суждениями 1. Постройте логический квадрат. Опираясь на него, выведите суждения, вступающие в логические отношения с данным суждением. Установите их истинность или ложность, исходя из условия, что исходное суждение является истинным. А) «Всякая наука имеет свой предмет исследования». Решение. Записываем логическую форму суждения: «Все S есть Р», где S - «наука», Р - «имеет свой предмет исследования». Данное суждение общеутвердительное (А). 1) Отношение противоположности.
По логическому квадрату в отношении противоположности Следовательно, противоположным по отношению к исходному суждению будет суждение: «Ни одна наука не имеет свой предмет исследования». Логическая форма: «Ни одно S не есть Р» (Е). Исходя из отношений по логическому квадрату данное суждение необходимо ложно. 2) Отношение подчинения. В отношении логического подчинения находятся суждения вида А и I, а также Е и О. Истинность общего суждения определяет истинность частного, подчиненного суждения. Ложность общего суждения оставляет частное суждение неопределенным. Истинность частного суждения оставляет общее суждение неопределенным. Следовательно, в отношении логического подчинения к исходному суждению находится суждение: «Некоторые науки имеют свой предмет исследования». Логическая форма «Некоторые S есть Р» (I). Исходя из отношений суждений по логическому квадрату данное суждение необходимо истинно. 3) Отношения противоречия. В отношении противоречия находятся суждения вида А и О, а также Е и I. Два противоречащих суждения не могут быть одновременно истинными и одновременно ложными. Следовательно, в отношении противоречия к исходному суждению находится суждение: «Некоторые науки не имеют своего предмета исследования». Логическая форма: «Некоторые Sесть Р» (О). Исходя из отношений по логическому квадрату данное суждение необходимо ложно.
2. Определите по логическому квадрату отношения между суждениями и установите их истинность или ложность: «Некоторые открытия ведут к новым проблемам». - «Некоторые открытия не ведут к новым проблемам». Решение. Определим типы суждений: первое суждение - I, второе - О. Отношение между ними субконтрарность (частичное совпадение). В этом отношении суждения вида I и О, имеют одинаковые субъекты и одинаковые предикаты, но различаются по качеству. Оба они одновременно могут быть истинными, но не могут быть одновременно ложными. Если одно из них ложно, то другое необходимо истинно. Однако, если одно из них
3. Определите с помощью «логического квадрата» отношения между следующими простыми суждениями: «Некоторые планеты не имеют атмосферы» и «Не все планеты имеют атмосферу». Решение. Суждение «Некоторые планеты не имеют атмосферы» представлено в явной логической форме. Его логическая форма: Некоторые S не есть Р - это частноотрицательное суждение (О), где «планеты» - S «имеют атмосферу» - Р. Суждение «Не все планеты имеют атмосферу» нужно привести к явной логической форме: «Не верно, что все планеты имеют атмосферу». Его логическая формула: Неверно (Все S есть Р) = (Все S есть Р). Отрицанием УМОЗАКЛЮЧЕНИЯ 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

 В) Некоторая девушка красива.
В) Некоторая девушка красива.




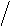 Решение. Формула х (Р(х) → Q(х)). Буквальный смысл этой записи «Для всякого
Решение. Формула х (Р(х) → Q(х)). Буквальный смысл этой записи «Для всякого  объекта (человека) верно, что если она девушка, то она красива».
объекта (человека) верно, что если она девушка, то она красива».















 Решение. Данное предложение является простым атрибутивным выделяющим суждением.
Решение. Данное предложение является простым атрибутивным выделяющим суждением.
