
|
|
НЕКОТОРЫЕ МЕТОДЫ ЧИСЛЕННОГО РЕШЕНИЯ СИСТЕМ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ.Содержание работы и порядок выполнения
Задача, предлагаемая в курсовой работе – задача прямого моделирования – получение однозначного решения при условии, что математическая модель определена полностью, т. е. известны все параметры модели, начальные условия, задается: 1. Схема механизма химической реакции. 2. Константы скоростей отдельных стадий реакций. 3. Начальные концентрации компонентов. 4. Продолжительность реакции. 5. Метод численного решения дифференциальных уравнений кинетики. Требуется: 1. Составить кинетическую модель данной химической реакции. 2. Выполнить на калькуляторе численное решение дифференциальных уравнений кинетики с целью получения кинетических зависимостей компонентов реакции в виде таблиц и графиков функций Сi (t) для пяти равноотстоящих значение t. 3. Выполнить программирование задачи для ЦВМ на алгоритмическом языке Паскаль. 4. Решить задачу на ЦВМ для 20 равноотстоящих значений t.
1.2. Содержание и оформления отчета. Отчет по лабораторной работе должен включать формулировку задания, а также подробное описание порядка выполнения работы в соответствии с предыдущим разделом « Содержание и порядок выполнения ». В отчете должны быть представлены: система дифференциальных уравнений, представляющая кинетическую модель данной химической реакции; описание метода численного решения системы дифференциальных уравнений; результаты численного решения задачи на калькуляторе в виде таблиц, графиков; Паскаль-программа решения задачи; результаты решения задачи на ЦВМ в виде таблиц и графиков решений, построенных на миллиметровой бумаге. Отчет оформляется лабораторной тетради.
ПОСТАНОВКА ЗАДАЧИ. Маршрут химической реакции принято отражать с помощью стехиометрического уравнения, которое показывает, в каких соотношениях вещества вступают во взаимодействие. Компоненты реакции обозначают буквами A,B,C,…
Если стехиометрическое уравнение отражает механизм химической реакции, то оно служит основанием для составления кинетических уравнений. Кинетические уравнения определяют связь между скоростью химической реакции концентрациями реагирующих веществ. Кинетические уравнения записываются на основании закон действующих масс, в соответствии с которым, скорость химической реакции пропорциональна концентрациям взаимодействующих веществ и не зависит от концентрации продуктов. Так, для приведенного выше стехиометрического уравнения имеем:
Здесь К – константа скорости химической реакции. Решая систему дифференциальных уравнений с некоторыми заданными начальными условиями СА(О) = САО , СВ(О) = СВО , СС(О) = ССО , получим кривые зависимости СА(t) , СВ(t) , СС(t) – кинетические кривые, таким образом, можем рассчитать концентрации компонентов в определенный момент времени.
НЕКОТОРЫЕ МЕТОДЫ ЧИСЛЕННОГО РЕШЕНИЯ СИСТЕМ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ. Математическое моделирование кинетики сложных химических реакций сводится к решению систем обыкновенных дифференциальных уравнений вида:
с начальными условиями yi(x0) = yio , где i = 1,…,К. Как правило, система уравнений, описывающих кинетику изучаемой реакции, является нелинейной и поэтому не может быть решена аналитически. Возникает необходимость использования метод приближенного численного интегрирования. Эти методы позволяют приближенно отыскать решения дифференциальных уравнений только на некотором конечном интервале [a; b]. Пусть имеем некоторое дифференциальное уравнение первого порядка y=f(x;y) с начальными условиями y(x0)=y0. Будем искать решение этого уравнения на отрезке [x0;b]. Разобьем этот отрезок на n равных частей. Тогда получим систему равноотстоящих узлов x0 , x1=x0+h, x2=x1+h, …, xn=b. Здесь h=(b-x0)/n – шаг интегрирования. Численные методы дают возможность найти в некотором числе точек x1, x2, …, xn приближения y1, y2, …, yn для значений точного решения y(x1), y(x2), …, y(x0) . Наиболее простым методом решения дифференциальных и их систем является
3.1 МЕТОД ЭЙЛЕРА.
Пусть дано дифференциальное уравнение y'=f(x,y) (1), с начальными условиями y(x0)=y0 . Пусть y=y(x) – искомое точное решение. Интегральная кривая проходит через точку (x0,y0). Найдем приближенные значения функции в точках x1, x2, …, xn. Построим систему равноотстоящих точек x0, x1=x0+h, …, xn=b. Проведём прямые x=x0, x=x1, …, x=b.

Рассмотрим отрезок [x0,x1]. На этом отрезке есть одна точка, которая принадлежит искомой кривой – это точка А (x0,y0). Заменим дугу искомой кривой y=y(x) на отрезке [x0,x1] касательной к ней, проведенной в точке (x0,y0). В качестве y1 возьмём ординату точки пересечения прямой x=x1 к касательной. Очевидно y1=y0+h•tgα0. Но tgα0=y'(x0), т.е. y1=y0+h•y'(x0). Но из уравнения (1) следует, что y'(x0)=f(x0,y0). Итак, получаем y1=y0+h•f(x0,y0), x1=x0+h . Предположим теперь, что точка (x1,y1) принадлежит искомой кривой. В этой точке опять проведём касательную к графику функции до пересечения с прямой x=x2 . Тогда аналогично: y2= y1+ h f(x1,y1); x2= x1+ h . Продолжая и так далее, получим систему значений y1,y2,…,yn, которые и будут приближенными значениями функции y=y(x) в точках x1,x2,…xn. Итак, расчётные формулы метода Эйлера: ym+1= ym+ h f(xm,ym); xm+1= xm+ h Для системы дифференциальных уравнений y'I = fi(x,y1,y2,…yk) yi(x0) = yi0 i = 1,…,K расчетные формулы записываются аналогично yim+1 = yim + hfi(x,y1m,y2m,…ykm); xm+1 = xm+ h, здесь i – номер уравнения в системе, n – номер шага. Метод Эйлера является грубым методом, ошибка, которую мы допускаем, на каждом шаге, пропорциональна h, т.е. |y(xk) - yk|≈ h. Чтобы повысить точность вычислений, используют некоторые усовершенствованные методы. 3.2. МЕТОД ЭЙЛЕРА-КОШИ
Пусть опять решаем уравнение y'= f(x,y), y(x0)= y0. Решение ищем на отрезке [x0,xn]. Пусть нам известны координаты некоторой точки, принадлежащей искомому решению (xm,ym). Найдём средний тангенс угла наклона касательной для двух точек: (xm,ym) и (xm+h,ym+h·ỹm). Последняя точка, есть та самая, которую в методе Эйлера мы обозначаем (xm+1,ym+1), но здесь точка будет вспомогательной. ỹm+1
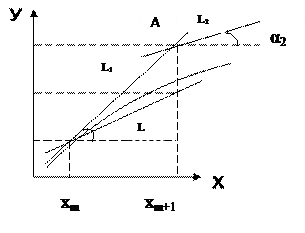
Итак, сначала по методу Эйлера находится точка А, лежащая на прямой L1, тангенс угла наклона которой tgα1= f(xm,ym). В этой точке снова вычисляется тангенс угла наклона касательной L2 tgα2= f(xm+h,ym+hỹm) Затем через точку (xm,ym) проводим прямую L, тангенс угла наклона которой равен (tgα1+tgα2)/2. Точка, в которой L пересекается с прямой x=xm+1 и будет искомой (xm+1,ym+1). Таким образом, ym+1 есть искомое приближение значений функции на данном шаге интегрирования. Расчетные формулы метода Эйлера-Коши следующие: ỹm+1= ym+hf(xm,ym); ym+1= ym+(h/2)·[f(xm,ym)+f(xm+1,ỹm+1)]; xm+1= xm+h. Аналогично, для системы дифференциальных уравнений: yi'= fi(x,y1,y2,…yk), yi(x0)=yio, i=1,2,..k; ỹim+1= yim+ hfi(xm,y1m,y2m,…ykm); yim+1= yim+ (h/2)·[fi(xm,y1m,y2m,…ykm)+fi(xm+1,ỹ1m+1,ỹ2m+1,ỹkm+1)]; xm+1= xm+h. Здесь i – номер уравнения системы, m – номер шага.
ПРОГРАММА МЕТОДА ЭЙЛЕРА.
PROGRAM EILER; USES CRT; VAR C, Z: ARRAY[1..4] OF REAL; I: INTEGER; T, TMAX: REAL; BEGIN CLRSCR; WRITE (‘TMAX=’); READLN (TMAX); T:=0; WRITE (‘ВВЕДИТЕ С1, С2, С3, С4’); READLN(C[1]); READLN(C[2]); READLN(C[3]); READLN(C[4]); WRITELN (‘T C1 C2 C3 C4’); WHILE T<=TMAX DO BEGIN Z[1]:={ПРАВАЯ ЧАСТЬ ПЕРВОГО УРАВНЕНИЯ СИСТЕМЫ}; Z[2]:={ПРАВАЯ ЧАСТЬ ВТОРОГО УРАВНЕНИЯ СИСТЕМЫ}; Z[3]:={ПРАВАЯ ЧАСТЬ ТРЕТЬЕГО УРАВНЕНИЯ СИСТЕМЫ}; Z[4]:={ПРАВАЯ ЧАСТЬ ЧЕТВЁРТОГО УРАВНЕНИЯ СИСТЕМЫ}; T:=T+0.5; WRITE (T:5:1); FOR I:=1 TO 4 DO WRITE (Z[1]:10:5); WRITELN; FOR I:=1 TO 4 DO C[I]:=Z[I]; END; READKEY; END.
Program Eiler; Uses Crt; Type Vec=Array[1..6] of Real;
Var y, k, f:Vec; i, KolKom, KolRec, KolForPrint,count:Byte; x, xk, h, s:Real; Fout:text; NameOut:string[12]; Procedure f_dir(y:vec; var f:vec); var r:vec; begin r[1]:=k[1]*y[1]; r[2]:=k[2]*y[2]; r[3]:=k[3]*y[2]; r[4]:=k[4]*y[3]; r[5]:=k[5]*y[2]; f[1]:=-r[1]+r[5] ; f[2]:=r[1]-r[2]-r[3]+r[4]-r[5]; f[3]:=r[2]-r[4]; f[4]:=r[3] end;
BEGIN ClrScr; x:=0; xk:=15; h:=0.1;count:=0;s:=0;
write('введите количество компонентов ');readln(KolKom); For i:=1 to KolKom do begin write(введите концентрации компонентов');readln(y[i]) end; write('введите количество химических реакций ');readln(KolRec); For i:=1 to KolRec do begin write(введите константы химической реакции');readln(k[i]) end; write('введите число точек для вывода значения на экран'); readln(KolForPrint); write('введите имя файлов для результатов'); readln(NameOut); ClrScr; assign(fout,NameOut); rewrite(fout); write('время');write(fout,'время'); For i:=1 to KolKom do begin write(' y[',i,']'); write(fout,' y[',i,']'); end; writeln(' сумма '); writeln(fout,' сумма '); write(x:5:1);write(fout,x:5:1); for i:=1 to KolKom do begin s:=s+y[i];write(y[i]:8:5);write(fout,y[i]:8:5) end; writeln(s:8:2);writeln(fout,s:8:2);
repeat f_dir(y,f); For i:=1 to KolKom do y[i]:=y[i]+h*f[i]; x:=x+h; count:=count+1; if count=round(xk/h/KolForPrint) then begin write(x:5:1);write(fout,x:5:1);s:=0; for i:=1 to KolKom do begin s:=s+y[i];write(y[i]:8:5);write(fout,y[i]:8:5); end; writeln(s:8:2);writeln(fout,s:8:2);count:=0 end; until x>xk; close(fout); readkey end. ПРОГРАММА МЕТОДА ЭЙЛЕР-КОШИ Program Eiler_Koshi; Uses Crt; Type MAS=Array[1..6] of Real; Var y, y0,k, f0,f:MAS; i, KolKom, KolRec, KolForPrint, count:Byte; x xk, h, s:Real; Fout:text; NameOut:string[12];
Procedure f_dir(y:vec; var f:vec); var r:vec; begin r[1]:=k[1]*y[1]; r[2]:=k[2]*y[2]; r[3]:=k[3]*y[2]; r[4]:=k[4]*y[3]; r[5]:=k[5]*y[2]; f[1]:=-r[1]+r[5] ; f[2]:=r[1]-r[2]-r[3]+r[4]-r[5]; f[3]:=r[2]-r[4]; f[4]:=r[3] end;
BEGIN ClrScr; x:=0; xk:=15; h:=0.1;count:=0;s:=0;
write('введите количество компонентов ');readln(KolKom); For i:=1 to KolKom do begin write(‘введите концентрацию компонента');readln(y[i]) end; write('введите количество химических реакций ');readln(KolRec); For i:=1 to KolRec do begin write('введите константы химической реакции');readln(k[i]) end; write('введите число точек для вывода значений на экран '); readln(KolForPrint); write('введите имя файла для результатов'); readln(NameOut); ClrScr; assign(fout,NameOut); rewrite(fout);
write(' время');write(fout,' время'); For i:=1 to KolKom do begin write(' y[',i,']'); write(fout,' y[',i,']'); end; writeln(' сумма '); writeln(fout,' сумма '); write(x:5:1);write(fout,x:5:1); for i:=1 to KolKom do begin s:=s+y[i];write(y[i]:8:5);write(fout,y[i]:8:5) end; writeln(s:8:2);writeln(fout,s:8:2);
repeat f_dir(y,f); For i:=1 to KolKom do begin y0[i]:=y[i]; f0[i]:=f[i]; y[i]:=y0[i]+h*f[i]; end; f_dir(y,f); For i:=1 to KolKom do y[i]:=y0[i]+0.5*h*(f0[i]+f[i]); x:=x+h; count:=count+1; if count=round(xk/h/KolForPrint) then begin write(x:5:1);write(fout,x:5:1);s:=0; for i:=1 to KolKom do begin s:=s+y[i];write(y[i]:8:5);write(fout,y[i]:8:5); end; writeln(s:8:2);writeln(fout,s:8:2);count:=0 end; until x>xk; close(fout); readkey end.
3.3. МЕТОД РУНГЕ-КУТТА 2-ГО ПОРЯДКА
Пусть имеем дифференциальное уравнение y'=f(x,y) с начальными условиями у(x0)=y0. Ищем решение на отрезке [x0,xn]. Пусть имеем точку (xm,ym), принадлежащему искомому решению. Для того, чтобы найти следующую точку проведем касательную к кривой в точке (xm,ym) до пересечения с прямой x=xm+0.5, где xm+0.5=xm+h/2. Тогда получим координату (по формуле Эйлера) ym+0.5=ym+h/2·f(xm,ym). Теперь найдём тангенс угла наклона касательной в т.В (xm+0.5,ym+0.5), (прямая L). Через точку А проведём прямую L'||L. Ординату точки пересечения прямых L' и x=xm+1 возьмём в качестве ym+1. Таким образом ym+0.5= ym+h/2·f(xm,ym), xm+0.5=xm+h/2 ym+1= ym+h·f(xm+0.5,ym+0.5), xm+1=xm+h Для системы дифференциальных уравнений yi'= fi(x,y1,y2,…yk), yi(x0)= yi0, i= 1,2,…k расчетные формулы имеют вид: yim+0.5= yim+h/2·fi(xm,y1m,y2m,…ykm), xm+0.5= xm+h/2; yim+1= yim+h·fi(xm+0.5,y1m+0.5,y2m+0.5,…ykm+0.5); xm+1= xm+h.
ПРОГРАММА РУНГЕ-КУТТА 2-ГО ПОРЯДКА Program Runge_Kutte_Method; Uses Crt; Type Vec=Array[1..6] of Real; Var y, y0, k, f:Vec; i, KolKom, KolRec, KolForPrint, count:Byte; x, xk, h, s:Real; Fout:text; NameOut:string[12];
Procedure f_dir(y:vec; var f:vec); var r:vec; begin r[1]:=k[1]*y[1]; r[2]:=k[2]*y[2]; r[3]:=k[3]*y[2]; r[4]:=k[4]*y[3]; r[5]:=k[5]*y[2]; f[1]:=-r[1]+r[5] ; f[2]:=r[1]-r[2]-r[3]+r[4]-r[5]; f[3]:=r[2]-r[4]; f[4]:=r[3] end;
BEGIN ClrScr; x:=0; xk:=15; h:=0.1;count:=0;s:=0;
write('введите количество компонентов ');readln(KolKom); For i:=1 to KolKom do begin write(i,’введите концентрации компонентов ');readln(y[i]) end; write('введите количество химических реакций ');readln(KolRec); For i:=1 to KolRec do begin write(i,'введте константы химических реакции');readln(k[i]) end; write('введите число точек для вывода значения на экран '); readln(KolForPrint); write('введите имя файлов для результатов'); readln(NameOut); ClrScr; assign(fout,NameOut); rewrite(fout);
write(' время ');write(fout,' время '); For i:=1 to KolKom do begin write(' y[',i,']'); write(fout,' y[',i,']'); end; writeln(' сумма '); writeln(fout,' сумма '); write(x:5:1);write(fout,x:5:1); for i:=1 to KolKom do begin s:=s+y[i];write(y[i]:8:5);write(fout,y[i]:8:5) end; writeln(s:8:2);writeln(fout,s:8:2);
repeat f_dir(y,f); For i:=1 to KolKom do begin y0[i]:=y[i]; y[i]:=y0[i]+0.5*h*f[i]; end; f_dir(y,f); For i:=1 to KolKom do y[i]:=y0[i]+h*f[i]; x:=x+h; count:=count+1; if count=round(xk/h/KolForPrint) then begin write(x:5:1);write(fout,x:5:1);s:=0; for i:=1 to KolKom do begin s:=s+y[i];write(y[i]:8:5);write(fout,y[i]:8:5); end; writeln(s:8:2);writeln(fout,s:8:2);count:=0 end; until x>xk; close(fout);
readkey end.
3.4. МЕТОД РУНГЕ-КУТТА 4-ГО ПОРЯДКА Этот метод один из самых распространённых методов интегрирования дифференциальных уравнений. Для одиночного дифференциального уравнения y'= f(x,y), y(x0)=y0 расчётные формулы имеют следующий вид: ym+1= ym+h/6(k1+2k2+2k3+k4), где k1= f(xm,ym); k2= f(xm+ k3= f(xm+ k4= f(xm+h,ym+hk3); xm+1= xm+h. Для системы дифференциальных уравнений yi'= fi(x,y1,y2,…yk), yi(x0)=yi0, i=1,2,..k, расчетные формулы запишутся следующим образом: yim+1= yim+ где k1i= fi(xm,y1m,y2m,…ykm); k2i= fi(xm+h/2,y1m+ k3i= fi(xm+ k4i= fi(xm+h,y1m+hk31,y2m+hk32,…ykm+hk3k). PROGRAM RYNGE_KYTT; USES CRT; VAR X,X0,Y0,XMAX:REAL; YT,DY,K1,K2,K3,K4:REA; H:REAL; I,N:LONGINT;
FUNCTION F(X,Y:REAL):REAL; BEGIN F:=(-2*Y/X+EXP(-X*X)/X; END;
BEGIN WRITE(‘H=’); READLN(H); WRITE(‘X0=’); READLN(X0); WRITE(‘XMAX=’); READLN(XMAX); WRITE(‘Y0=’); READLN(Y0); N:=ROUND((XMAX-X0)/H); YT:=-EXP(-X0*X0)/(2*X0*X0)+15/(X0*X0); WRITELN(‘X0=’,X0:8:4,’ Y0=YT= ’,YT:8:4); FOR I:=1 TO N DO BEGIN K1:=F(X0,Y0); K2:=F(X0+H/2,Y0+H*K1/2); K3:=F(X0+H/2,Y0+H*K2/2); K4:=F(X0+H,Y0+H*K3); Y0:=Y0+H/6*(K1+2*K2+2*K3+K4); X0:=X0+H; YT=-EXP(-X0*X0)/(2*X0*X0)+15/(X0*X0); DY:=ABS(YT-Y0); WRITELN(‘X=’,X0:8:4,’YT=’,YT:8:4,’YR=’,YO:8:4,’DY=’,DY:10:8); END; READKEY; END.
Program Runge_Kutte_4_Method; Uses Crt; Type =Array[1..6] of Real; Var y, y0, k, ka, f:Vec; i, KolKom, KolRec, KolForPrint, count:Byte; x, xk, h, s:Real; Fout:text; NameOut:string[12];
Procedure f_dir(y:vec; var f:vec); var r:vec; begin r[1]:=k[1]*y[1]; r[2]:=k[2]*y[2]; r[3]:=k[3]*y[2]; r[4]:=k[4]*y[3]; r[5]:=k[5]*y[2]; f[1]:=-r[1]+r[5] ; f[2]:=r[1]-r[2]-r[3]+r[4]-r[5]; f[3]:=r[2]-r[4]; f[4]:=r[3] end;
BEGIN ClrScr; x:=0; xk:=15; h:=0.1;count:=0;s:=0;
write('введите количество компонентов ');readln(KolKom); For i:=1 to KolKom do begin write(i,'введите концентрации компонентов');readln(y[i]); y0[i]:=y[i] end; write('введите количество химических реакций ');readln(KolRec); For i:=1 to KolRec do begin write(i,'введите константы химической реакции ');readln(k[i]) end; write(' введите число точек для вывода значения на экран '); readln(KolForPrint); write('введите имя файла для результатов '); readln(NameOut); ClrScr; assign(fout,NameOut); rewrite(fout);
write('время');write(fout,' время '); For i:=1 to KolKom do begin write(' y[',i,']'); write(fout,' y[',i,']'); end; writeln(' сумма '); writeln(fout,' сумма'); write(x:5:1);write(fout,x:5:1); for i:=1 to KolKom do begin s:=s+y[i];write(y[i]:8:5);write(fout,y[i]:8:5) end; writeln(s:8:2);writeln(fout,s:8:2);
repeat f_dir(y,f); For i:=1 to KolKom do begin ka[i]:=h*f[i]; y[i]:=y0[i] + ka[i]/2; end; f_dir(y,f); For i:=1 to KolKom do begin ka[i]:=ka[i] + 2*h*f[i]; y[i]:=y0[i] + h*f[i]/2; end; f_dir(y,f); For i:=1 to KolKom do begin ka[i]:=ka[i] + 2*h*f[i]; y[i]:=y0[i] + h*f[i]; end; f_dir(y,f); For i:=1 to KolKom do begin y[i]:=y0[i] + (ka[i] + h*f[i])/6; y0[i]:=y[i] end; x:=x+h; count:=count+1; if count=round(xk/h/KolForPrint) then begin write(x:5:1);write(fout,x:5:1);s:=0; for i:=1 to KolKom do begin s:=s+y[i];write(y[i]:8:5);write(fout,y[i]:8:5); end; writeln(s:8:2);writeln(fout,s:8:2);count:=0 end; until x>xk; close(fout); readkey end.
4. МОДЕЛИРОВАНИЕ КИНЕТИКИ ХИМИЧЕСКОЙ РЕАКЦИИ Пример. Задано: 1. Схема механизма химической реакции
К1 К2
Д
2. Константы скоростей отдельных стадий реакции К1 = 0,76 с-1 К2 = 0,9 с-1 К3 = 0,5 с-1 К4 = 0,45 с-1 К5 = 0,6 с-1 3. Начальные концентрации компонентов СА(0) = 0,7 моль/л СВ(0) = 0 СС(0) = 0 СД(0) = 0 4. Продолжительность реакции 15 секунд 5. Метод численного решения – Эйлера. Выполнение работы: 1. Система дифференциальных уравнений, представляющая кинетическую модель данной химической реакции:
2. Расчетные формулы метода Эйлера: CAm+1= CAm+h(-K1CAm+K5CBm); CBm+1= CBm+h(-K2CBm+K1CAm+K4CCm-K5CBm-K3CBm); CCm+1= CCm+h(K2CBm-K4CCm); CDm+1= CDm+h·K3CBm; tm+1= tm+h. 3. Результаты численного решения системы дифференциальных уравнений на калькуляторе. h = 0.2; 5 шагов по времени. Пример вычислений:
СA1 = 0.7+0.2(-0.76*0.7+0.6*0)=0.5936; CB1 = 0+0.2(-0.2*0+0.76*0.7+0.45*0-0.6*0-0.5*0)=0.01064 CC1 = 0+0.2(0.9*0-0.45*0)=0; CD1=0+0.2(0.5*0)=0; t=0+0.2=0.2 Аналогично вычисляем СА2, СВ2, СС2, СД2,…СА5, СВ5, СС5, СД5.
Таблица результатов расчёта
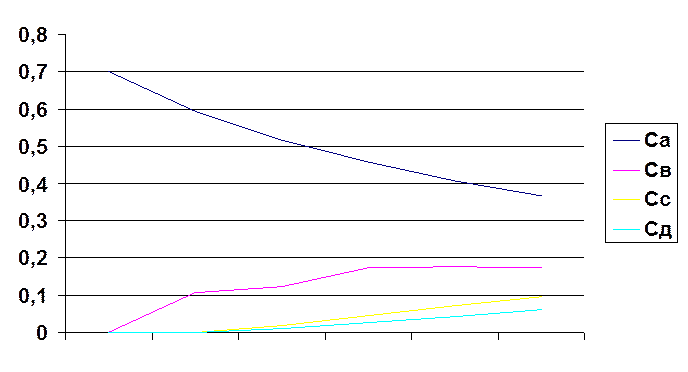
Графики кинетических кривых
PROGRAM EILER; USES CRT; VAR C, Z: ARRAY[1..4] OF REAL; I: INTEGER; T, TMAX: REAL; BEGIN CLRSCR; WRITE (‘TMAX=’); READLN (TMAX); T:=0; WRITE (‘ВВЕДИТЕ С1, С2, С3, С4’); READLN(C[1]); READLN(C[2]); READLN(C[3]); READLN(C[4]); WRITELN (‘T C1 C2 C3 C4’); WHILE T<=TMAX DO BEGIN Z[1]:=C[1]+0.2*(-0.76*C[1]+0.6C[2]); Z[2]:=C[2]+0.2*(-0.9*C[2]+0.76*C[1]+0.45*C[3]-0.6*C[2]-0.5*C[2]); Z[3]:=C[3]+0.2*(0.9*C[2]-0.45*C[3]); Z[4]:=C[4]+0.2*0.5*C[2]; T:=T+0.2; WRITE (T:5:1); FOR I:=1 TO 4 DO WRITE (Z[1]:10:5); WRITELN; FOR I:=1 TO 4 DO C[I]:=Z[I]; END; READKEY; END.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 Например, А + В С – стехиометрическое уравнение.
Например, А + В С – стехиометрическое уравнение.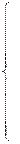
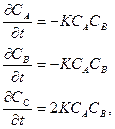

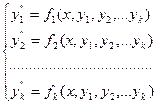
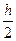 ,ym+
,ym+ 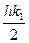 );
);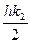 );
);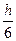 (k1i+2k2i+2k3i+k4i), i=1,2,…k,
(k1i+2k2i+2k3i+k4i), i=1,2,…k,
 А В С
А В С К5 К3 К4
К5 К3 К4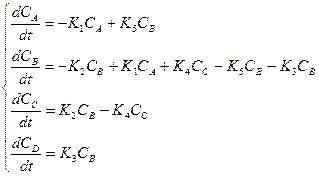

 4. ПАСКАЛЬ-программа решения системы дифференциальных уравнений
4. ПАСКАЛЬ-программа решения системы дифференциальных уравнений