
|
|
Расчётно-графическая работа«Линейная алгебра и аналитическая геометрия» Задание 1. Найти область решения системы неравенств. Сделать чертеж. 1.
4.
7.
10.
13.
16.
19.
22.
25. Задание 2. Решить систему уравнений двумя способами: 1) методом Гаусса; 2) матричным методом.
Задание 3. Дана пирамида 1) угол между ребрами 2) уравнение плоскости 3) уравнение и длину высоты, опущенной из вершины 4) угол между ребром 5) объем пирамиды 6) площадь грани. Сделать чертеж.
Задание 4. Даны векторы Показать, что векторы
Задание 5. Привести уравнение кривой второго порядка к каноническому виду. Сделать чертеж. Найти координаты вершин и фокусов. Построить директрисы кривой .
Задание 6. Дано комплексное число
Задание 7. Найти собственные векторы линейного преобразования, приводящего квадратичную форму к каноническому виду. Установить вид кривой и сделать чертеж. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25.
Пример выполнения варианта расчетно-графической работы. Задание 1.Найти область решения системы неравенств. Сделать чертеж.
Решение. Заменим в данной системе каждое неравенство равенством. По полученным уравнениям построим прямые. Каждая прямая разделит плоскость на две полуплоскости, в одной из которых выполняется неравенство, в другой - нет. Часть плоскости, в которой выполняются все неравенства и есть область решения.
Рис.1
Ответ. Областью решения служит четырехугольник ABCD.
Задание 2.Решить систему уравнений двумя способами: 1) Методом Гауcса 2) Матричным методом.
Решение. Вычислить определитель системы ∆: ∆=
Следовательно, система имеет единственное решение. Решим систему методом Гаусса. Составим расширенную матрицу, и, применяя элементарные преобразования, приведем ее к диагональному виду
Проверка:
Решим систему матричным методом. Составим обратную матрицу А-1. Вычислим алгебраическое дополнение Аίj:
Ответ: Задание 3.Дана пирамида Найти: 1)угол между ребрами 2)уравнение плоскости 3)уравнение и длину высоты, опущенной из вершины 4)угол между ребром 5)объем пирамиды; 6)площадь грани
Решение. 1)Найти координаты векторов
Вычислим косинус угла
2)Запишем уравнение плоскости, проходящей через три точки:
Уравнение плоскости 3)Вычислим векторное произведение векторов
Так как вектор векторного произведения перпендикулярен плоскости
Найдем координаты точки
Уравнение высоты запишем в параметрической форме и решим систему:
Вычислим длину высоты
Уравнение высоты
Длинна 4)Вычислим синус угла между ребром
5)вычислим объем пирамиды
6) Вычислим площадь грани
Сделаем чертеж:
Рис. 2
Задание 4.Даны векторы Показать, что векторы
Решение. Три вектора образуют базис в пространстве, если они некомпланарны. Условием компланарности трех векторов служит равенство Вычислим смешенное произведение:
Следовательно, векторы образуют базис. Найдем координаты вектора d в этом базисе. Разложение вектора Переходя к координатам записи, получим:
Решим систему по формуле Крамера: ∆=9 Найдем вспомогательные определители:
Искомое разложение имеет вид:
Задание 5.Привести уравнение кривой к каноническому виду. Сделать чертеж. Найти координаты фокусов и вершин.
Решение. Выделим полные квадраты по
Полученное уравнение - уравнение гиперболы. Центр симметрии в точке 0(0: 3). Действительная полуось гиперболы
Получим координаты фокусов:
Координаты вершин:
Рис.3 Задание 6.Дано комплексное число
Решение. Запишем комплексное число в алгебраической форме:
Найдем модуль комплексного числа:
Решим уравнение: Запишем число z в тригонометрической форме:
По правилу извлечения корня третьей степени из z ,получим:
Изобразим схематически полученные результаты.
Алгебраическая форма: Тригонометрическая форма: Корни уравнения:
Задание 7. Найти собственные векторы линейного преобразования, приводящего квадратическую форму Решение. Составим матрицу квадратной формы: Найдем собственные значения и собственные векторы линейного преобразования, определяемого матрицей А:
Найдем корни полученного уравнения:
Найдем собственные векторы, соответствующие собственным значениям:
Пусть Собственный вектор
Пусть Собственный вектор Составим матрицу преобразования:
Запишем формулы преобразования координат:
Поставим в квадратную форму:
Полученное уравнение описывает гиперболу. Действительная полуось гиперболы Сделаем чертеж.
Рис. 5
Содержание
1. Линейные уравнения и неравенства с двумя неизвестными………………….3 2. Системы линейных уравнений и неравенств с двумя неизвестными………..5 3. Матрицы и определители……………………………………………………….7 4. Определители произвольного порядка……………………………………….10 5. Системы линейных алгебраических уравнений……………………………..12 6. Методы решения системы линейных алгебраических уравнений………….14 7. Векторы и линейные операции над ними…………………………………….16 8. Умножение векторов…………………………………………………………...21 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 2.
2.  3.
3. 
 5.
5.  6.
6. 
 8.
8.  9.
9. 
 11.
11.  12.
12. 
 14.
14.  15.
15. 
 17.
17.  18.
18. 
 20.
20.  21.
21. 
 23.
23.  24.
24. 










 . Найти:
. Найти: и
и  ;
; ;
; на грань
на грань  ;
; и гранью
и гранью  ;
; ;
;





































































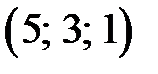





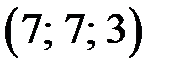







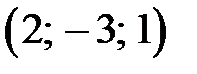
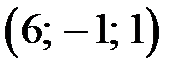














 и
и  в некотором базисе.
в некотором базисе. и
и  образуют базис и найти координаты вектора
образуют базис и найти координаты вектора 





















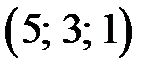














































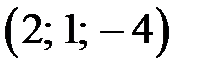









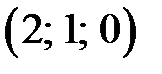














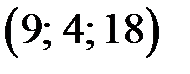






























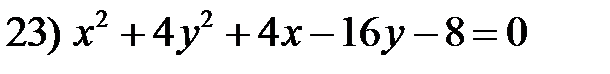







 . Записать комплексное число в алгебраической и тригонометрической формах. Найти все корни уравнения
. Записать комплексное число в алгебраической и тригонометрической формах. Найти все корни уравнения  . Результаты изобразить схематически.
. Результаты изобразить схематически.


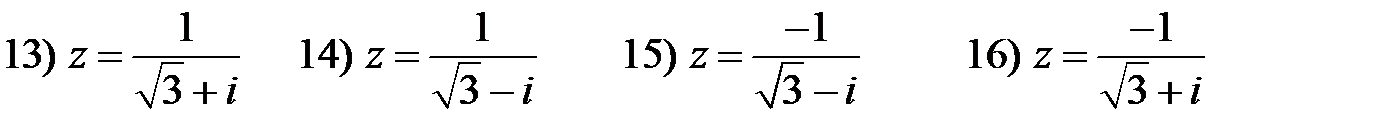































 =
= 

















 :
:  ,
,  ,
,  ,
,  .
. и
и  .
. ;
; на грань
на грань  ;
; и гранью
и гранью  ;
; . Сделать чертеж.
. Сделать чертеж. и
и 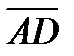 :
: =
= 

 =
= 


 =
= 

 образованного векторами
образованного векторами 






 и
и  :
:
 . Уравнения высоты будет иметь вид:
. Уравнения высоты будет иметь вид:
 , пересечения прямой
, пересечения прямой  с плоскостью
с плоскостью  . Запишем уравнение плоскости
. Запишем уравнение плоскости 






 ;
;  ;
; 
 :
:


 и гранью
и гранью 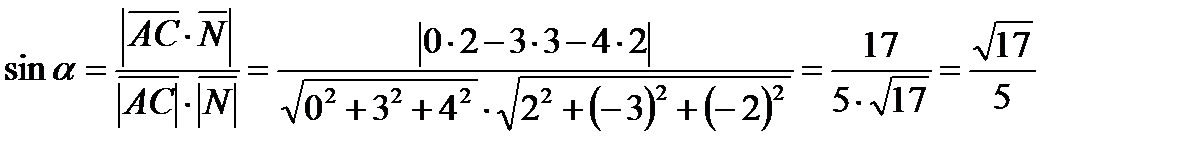
 рад.
рад.
 :
:
 ед.
ед. 
 :
: ед
ед 

 в некотором базисе.
в некотором базисе. образуют базис и найти координаты вектора
образуют базис и найти координаты вектора  в базисе
в базисе  .
. =
=  ,
,  =
=  ,
,  =
=  ,
,  =
= 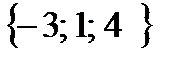


 в базисе
в базисе  , имеет вид:
, имеет вид:  =
= 






 ,
,  ,
, 
 +
+  -
- 
 .
. и
и  :
: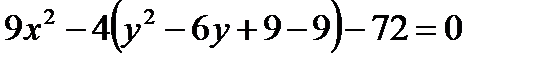


 ; мнимая полуось
; мнимая полуось  .
.
 ,
,  .
. ,
,  ,
,  ,
, 

 .Записать комплексное число в алгебраической и трибометрической формах. Найти все корни уравнений
.Записать комплексное число в алгебраической и трибометрической формах. Найти все корни уравнений  . Результат изобразить схематически.
. Результат изобразить схематически.





 .
.










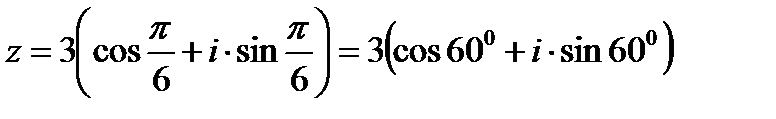



 к каноническому виду. Установить вид кривой и сделать чертеж.
к каноническому виду. Установить вид кривой и сделать чертеж.



 .
.

 , тогда
, тогда 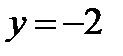
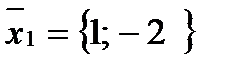 . Найдем единичный вектор:
. Найдем единичный вектор:  =
=  .
.

 , тогда
, тогда  .
. =
=  Единичный вектор:
Единичный вектор:  =
= 






 , мнимая полуось
, мнимая полуось  .
.