
|
|
Приведение общей кривой 2-го порядка к каноническому виду.Собственные векторы и собственные числа.
Опр.Пусть дано линейное преобразование
Замечание. Определение означает, что вектор Найдем собственные векторы и собственные значения. Для этого рассмотрим линейное пространство R с базисом
Подставим (7) и (8) в
собирая элементы при
Однородная система, всегда совместна. Если r<n имеет не нулевые решения, что возможно если минор максимального порядка равен нулю, Мn=0,то есть
Это выражение называется характеристическое уравнение. Решая его найдем собственные числа 2. Билинейные формы. Опр.Скалярная функция
Матрица билинейной формы. Найдём выражение билинейной формы в некотором базисе имеем j
Обозначим
Рассмотрим билинейную форму в пространстве R3 с базисом Тогда билинейная форма имеет вид
Получим матрицу билинейной формы Если базис ортонормированный, то матрица билинейной формы имеет вид: Определение. Билинейная форма называется симметричной (симметрической) если
Матрица симметричной билинейной формы
Линейные преобразования и билинейные формы. Пусть в пространстве R есть элементы Теорема . Для того, чтобы линейное преобразование Квадратичная форма. Определение. Если в билинейной форме
где Запишем квадратичную форму в R3.
учитывая, что
Приведение квадратичной формы к каноническому виду. Рассмотрим квадратичную форму
Пусть у нас есть ортонормированный базис
Говорят, что квадратичная форма (1) приведена к сумме квадратов или к каноническому виду. Пример: Привести к каноническому виду квадратичную форму.
Решение: Соответствующее этой форме симметричное линейное преобразование имеет матрицу.
Найдём собственные значения. Для этого составим характеристическое уравнение.
Приведение общей кривой 2-го порядка к каноническому виду. Рассмотрим уравнение.
Опр. Множество точек, координаты которых удовлетворяют уравнению (1) называется кривой 2-го порядка. Этими кривыми являются: эллипс, окружность, гипербола, парабола. В уравнении (1) группу старших членов можно рассматривать как квадратичную форму вектора
Мы уже знаем, что в некотором ортонормированном базисе
- где
Заметим, что коэффициенты данного характеристического уравнения и коэффициенты в уравнении кривой (1) не зависят от выбора базиса, и тем самым являются инвариантами, т.е. не меняются при переходе от одной системы координат к другой, итак:
Здесь
Из коэффициентов уравнения (1) можно составить определитель Тогда величины I1=
представляет эллиптический и гиперболический тип кривой. Здесь Уравнение Представляет параболический тип кривой. Здесь Таблица.
Пример: Определить тип кривой Составим матрицу Найдем инварианты Найдем третий инвариант

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 . Не нулевой вектор
. Не нулевой вектор  называется собственным вектором линейного преобразования, если
называется собственным вектором линейного преобразования, если 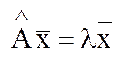 , где l - действительное число, оно называется собственным числом или собственным значением вектора
, где l - действительное число, оно называется собственным числом или собственным значением вектора  . Равенство
. Равенство  . (6)
. (6) .
. ,
,  , …,
, …,  и вектор
и вектор , (7)
, (7) . (8)
. (8) или учитывая (2) из предыдущей лекции, получим
или учитывая (2) из предыдущей лекции, получим
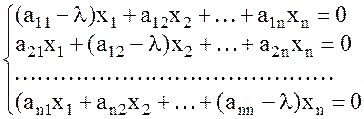 (9)
(9) (10)
(10) . Подставив их в систему (9) найдем собственные векторы
. Подставив их в систему (9) найдем собственные векторы  .
. двух векторных аргументов
двух векторных аргументов  называется билинейной формой, если она линейна по каждому аргументу, то есть
называется билинейной формой, если она линейна по каждому аргументу, то есть .
.


 j
j  в краткой записи
в краткой записи

 тогда:
тогда:

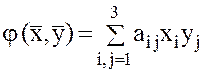
 или
или

 (символ Кронекера)
(символ Кронекера) или
или .
. .
. , то применим к вектору
, то применим к вектору  линейное преобразование
линейное преобразование  , получим вектор
, получим вектор  . Образуем скалярное произведение
. Образуем скалярное произведение  , получим:
, получим:  тогда билинейная форма
тогда билинейная форма  будет равна
будет равна  - скалярная функция векторных аргументов.
- скалярная функция векторных аргументов. было симметричным необходимо и достаточно, чтобы связанная с ним билинейная форма
было симметричным необходимо и достаточно, чтобы связанная с ним билинейная форма  была симметричной.
была симметричной. считать
считать  , то получим функцию
, то получим функцию 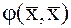 называемую квадратичной формой. Поскольку
называемую квадратичной формой. Поскольку 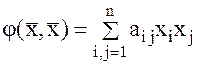
 - симметричная матрица.
- симметричная матрица.
 , получим
, получим выпишем матрицу квадратичной формы:
выпишем матрицу квадратичной формы: -это симметричная матрица.
-это симметричная матрица. , приведём соответствующее ей линейное преобразование
, приведём соответствующее ей линейное преобразование  , тогда:
, тогда: .
. тогда матрица квадратичной формы в ортонормированном базисе:
тогда матрица квадратичной формы в ортонормированном базисе: Здесь
Здесь  -собственные значения базисных векторов
-собственные значения базисных векторов  Разложим вектор
Разложим вектор  тогда скалярное произведение векторов есть:
тогда скалярное произведение векторов есть:  , тогда квадратичная форма примет вид
, тогда квадратичная форма примет вид  придадим значения индексам, получим:
придадим значения индексам, получим: (1).
(1).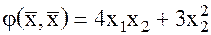


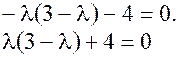
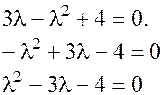
 Подставим найденные собственные значения в квадратичную форму
Подставим найденные собственные значения в квадратичную форму  .
.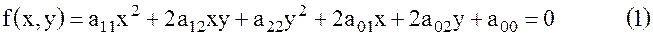
 , имеющего координаты х, у. Тогда
, имеющего координаты х, у. Тогда (2)
(2) данную квадратичную форму можно привести к каноническому виду:
данную квадратичную форму можно привести к каноническому виду: (3)
(3) и
и  собственные значения матрицы
собственные значения матрицы 
 Значение
Значение 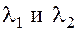 можно найти из характеристического уравнения
можно найти из характеристического уравнения (4)
(4) (5)
(5) ; (6)
; (6) . (7)
. (7)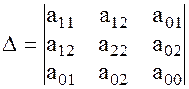 .
. (8)
(8) .
. (9)
(9)

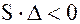 эллипс
эллипс
 мнимый эллипс
мнимый эллипс

 кривая
гиперболического
типа
кривая
гиперболического
типа
 кривая
параболического
типа
кривая
параболического
типа

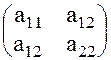 =
= 
 ;
;  , так как
, так как  , то из таблицы следует, что кривая эллиптического типа.
, то из таблицы следует, что кривая эллиптического типа. . Так как
. Так как  ;
;  ; Равенство равносильно системе
; Равенство равносильно системе ;
;  ; точка (-1;0)
; точка (-1;0)