
|
|
Приведение общей кривой 2-го порядка к каноническому виду.Лекция 5 1. Базис линейного пространства. 2. Линейные преобразования. 3. Матрица линейного преобразования. 4. Собственные векторы и собственные числа. 5. Билинейные формы. 6. Матрица билинейной формы. 7. Квадратичная форма. 8. Приведение общей кривой 2-го порядка к каноническому виду. Базис линейного пространства. Опр.: Совокупность nлинейно – независимых векторов образует базис линейного пространства.
Пример: Показать, что векторы
однородная система имеет тривиальное единственное решение, когда r=n=3, но это когда Линейные преобразования. Опр. Говорят, что в векторном пространстве L задан оператор Опр. Оператор 1. 2. Вектор Геометрический смысл свойств. Свойство 1 – означает, что диагональ параллелограмма, построенного на векторах
Свойство 2 - означает, что если вектор Следовательно, при линейном отображении коллинеарные вектора переходят в коллинеарные. Примеры линейных преобразований: 1.) Преобразование, которое вектор 2.) Преобразование, которое вектору Матрица линейного преобразования. Пусть в линейном пространстве L задан базис Собственные векторы и собственные числа. Опр.Пусть дано линейное преобразование
Найдем собственные векторы и собственные значения. Для этого рассмотрим линейное пространство R с базисом
Матрица линейного оператора
Матрица тождественного оператора
В результате получим однородную систему
Однородная система, всегда совместна. Если r<n имеет не нулевые решения, что возможно при Мn=0,то есть
Это выражение называется характеристическое уравнение. Решая его найдем собственные числа 5. Билинейные формы. Опр.Скалярная функция
Матрица билинейной формы. Найдём выражение билинейной формы в некотором базисе имеем в краткой записи j Обозначим j j Рассмотрим билинейную форму в пространстве R3 с базисом Тогда билинейная форма имеет вид
Квадратичная форма. Опр. Если в билинейной форме
где Запишем квадратичную форму в R3.
учитывая что
Приведём соответствующее ей линейное преобразование
Переходя к новой системе координат можно показать, что имеет место выражение:
Говорят, что квадратичная форма (5) приведена к сумме квадратов или к каноническому виду. Здесь Приведение общей кривой 2-го порядка к каноническому виду. Рассмотрим уравнение.
Опр. Множество точек, координаты которых удовлетворяют уравнению (6) называется кривой 2-го порядка. Этими кривыми являются: эллипс, окружность, гипербола, парабола. Введем инварианты. Обозначим:
Из коэффициентов уравнения (6) можно составить определитель
Тогда величины I1; I2; I3 будут инвариантами, т.е. не меняются при переходе от одной системы координат к другой. . Значение
Составим таблицу.
Пример: Определить тип кривой Составим матрицу Найдем инварианты S=1+1=2;

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
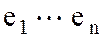 Теорема: Если образуют базис, то любой вектор
Теорема: Если образуют базис, то любой вектор  , можно представить в этом базисе, причем единственным образом в виде линейной комбинации базисных векторов
, можно представить в этом базисе, причем единственным образом в виде линейной комбинации базисных векторов
 ,
, 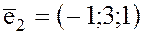 ,
,  образует базис.
образует базис. Решение: Если
Решение: Если  ,
,  ,
,  образуют базис, то они линейно независимы т.е. , при х1=х2=х3=0. Покажем это
образуют базис, то они линейно независимы т.е. , при х1=х2=х3=0. Покажем это ,
, 
 . Да, образует базис.
. Да, образует базис. или преобразование
или преобразование  поставлен в соответствие вектор
поставлен в соответствие вектор  .
. и числа
и числа  выполняется условие:
выполняется условие:
 .
. . Вектор
. Вектор  .
. отображается в диагональ
отображается в диагональ  параллелограмма, построенного на векторах
параллелограмма, построенного на векторах  .
.
 тоже увеличился в a раз.
тоже увеличился в a раз. .
. , является линейным. Геометрически преобразование
, является линейным. Геометрически преобразование  представляет собой однородное растяжение (сжатие) всех векторов пространства. Такое преобразование называется гомотетией.
представляет собой однородное растяжение (сжатие) всех векторов пространства. Такое преобразование называется гомотетией. ,
,  , …,
, …,  . Тогда любой вектор
. Тогда любой вектор  можно представить
можно представить  . Пусть в нашем пространстве задан линейный оператор
. Пусть в нашем пространстве задан линейный оператор  . Можно показать, что матрица оператора
. Можно показать, что матрица оператора 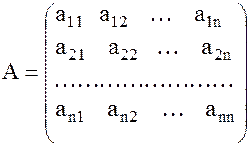 .
. . Равенство
. Равенство  . (1)
. (1) , (2)
, (2) есть
есть
 в этом же базисе
в этом же базисе  , так как он отображает вектор
, так как он отображает вектор  в
в  или
или .
. (3)
(3)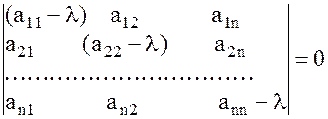 (4)
(4) . Подставив их в систему (3) найдем собственные векторы
. Подставив их в систему (3) найдем собственные векторы  .
. двух векторных аргументов
двух векторных аргументов  называется билинейной формой, если она линейна по каждому аргументу, то есть
называется билинейной формой, если она линейна по каждому аргументу, то есть .
.


 =j
=j  j
j 
 тогда:
тогда:

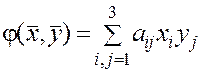

 Получим матрицу билинейной формы
Получим матрицу билинейной формы 
 считать
считать  , то получим функцию
, то получим функцию  называемую квадратичной формой. Поскольку
называемую квадратичной формой. Поскольку 
 - симметричная матрица.
- симметричная матрица.
 выпишем матрицу квадратичной формы:
выпишем матрицу квадратичной формы: -это симметричная матрица.
-это симметричная матрица. , тогда:
, тогда: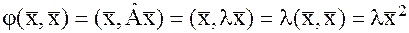 .
. (5).
(5). -собственные значения базисных векторов.
-собственные значения базисных векторов.
 ; (7)
; (7)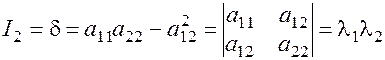 . (8)
. (8) (9)
(9) можно найти из характеристического уравнения
можно найти из характеристического уравнения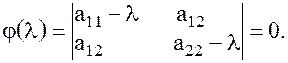 (10)
(10)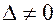
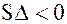 эллипс
эллипс
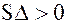 мнимый эллипс
мнимый эллипс

 кривая
гиперболического
типа
кривая
гиперболического
типа
 кривая
параболического
типа
кривая
параболического
типа

 =
= 
 кривая эллиптического типа.
кривая эллиптического типа. - точка. Найдем ее. Сгруппируем по х.
- точка. Найдем ее. Сгруппируем по х. ;
;  ;
; ;
;  ; точка (-1;0)
; точка (-1;0)