
|
|
Собственные векторы и собственные числа.Лекция 14 1. Евклидово пространство 2. Базис линейного пространства. 3. Линейные преобразования. 4. Матрица линейного преобразования. 5. Собственные векторы и собственные числа.
Евклидово пространство.
1. 2. 3. 4.
Опр.: Угол между векторами определим как Можно показать, что
Это можно показать с помощью неравенства Коши – Буняковского Базис линейного пространства. Опр.: Совокупность nлинейно – независимых векторов образует базис линейного пространства.
Пример: Показать, что векторы
однородная система имеет тривиальное единственное решение, когда r=n=3, но это когда Линейные преобразования. Опр. Говорят, что в векторном пространстве L задан оператор Опр. Оператор 1. 2. Вектор Геометрический смысл свойств. Свойство 1 – означает, что диагональ параллелограмма, построенного на векторах
Свойство 2 - означает, что если вектор Следовательно, при линейном отображении коллинеарные вектора переходят в коллинеарные. Примеры линейных преобразований: 1.) Преобразование (или оператор), которое вектор 2.) Преобразование, которое вектору Матрица линейного преобразования. Пусть в линейном пространстве L задан базис Собственные векторы и собственные числа. Опр.Пусть дано линейное преобразование
Найдем собственные векторы и собственные значения. Для этого рассмотрим линейное пространство R с базисом
Матрица линейного оператора
Матрица тождественного оператора
В результате получим однородную систему
Однородная система, всегда совместна. Если r<n имеет не нулевые решения, что возможно при условии, что минор n-го порядка Мn=0, то есть
Это выражение называется характеристическое уравнение. Решая его найдем собственные числа (собственные значения) Схема решения задач. 1. Составляем характеристическое уравнение (4) и находим его корни, которые являются собственными значениями матрицы. 2. Подставляем поочередно полученные собственные значения в систему (3). Если уравнение (4) имеет два различных корня, то получим два собственных вектора соответственно для каждого значения 3. Если корни уравнения (4) – 4. Если имеется пара корней уравнения (4) – 5. Если имеется пара корней уравнения (4) – Замечание. Симметричные матрицы второго порядка
всегда имеют два действительных собственных значения, причем при
6. Билинейные формы. Опр.Скалярная функция

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 Опр.: Линейное пространство называется Евклидовым, если в нем определена операция скалярного умножения: любым двум векторам
Опр.: Линейное пространство называется Евклидовым, если в нем определена операция скалярного умножения: любым двум векторам  ,
, 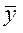 из Lсопоставляется число (
из Lсопоставляется число ( 


 , из условия
, из условия  , вытекает, что
, вытекает, что 
 Опр.: Длиной, модулем или нормой вектора в Евклидовом пространстве называется:
Опр.: Длиной, модулем или нормой вектора в Евклидовом пространстве называется:

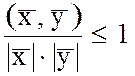
 .
. Теорема: Если образуют базис, то любой вектор
Теорема: Если образуют базис, то любой вектор 
 ,
,  ,
,  образует базис.
образует базис.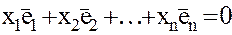 Решение: Если
Решение: Если  ,
,  ,
,  образуют базис, то они линейно независимы т.е. , при х1=х2=х3=0. Покажем это
образуют базис, то они линейно независимы т.е. , при х1=х2=х3=0. Покажем это ,
, 
 . Да, образует базис.
. Да, образует базис. или преобразование
или преобразование  поставлен в соответствие вектор
поставлен в соответствие вектор 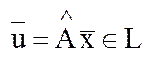 .
. и числа
и числа  выполняется условие:
выполняется условие:
 .
. . Вектор
. Вектор  .
. отображается в диагональ
отображается в диагональ  параллелограмма, построенного на векторах
параллелограмма, построенного на векторах 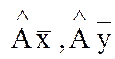 .
.
 тоже увеличился в a раз.
тоже увеличился в a раз. .
. , является линейным. Геометрически преобразование
, является линейным. Геометрически преобразование  представляет собой однородное растяжение (сжатие) всех векторов пространства. Такое преобразование называется гомотетией.
представляет собой однородное растяжение (сжатие) всех векторов пространства. Такое преобразование называется гомотетией. ,
,  , …,
, …, 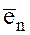 . Тогда любой вектор
. Тогда любой вектор 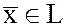 можно представить
можно представить  . Пусть в нашем пространстве задан линейный оператор
. Пусть в нашем пространстве задан линейный оператор  . Можно показать, что матрица оператора
. Можно показать, что матрица оператора  .
. . Равенство
. Равенство  . (1)
. (1) , (2)
, (2) есть
есть
 в этом же базисе
в этом же базисе  , так как он отображает вектор
, так как он отображает вектор  в
в  или
или .
. (3)
(3) (4)
(4) . Подставив их в систему (3) найдем собственные векторы
. Подставив их в систему (3) найдем собственные векторы  .
. .
. – действительные и различные, то мы получим собственные векторы с действительными координатами.
– действительные и различные, то мы получим собственные векторы с действительными координатами. – действительные и равные (кратные), то мы можем получим один собственный вектор с действительными координатами.
– действительные и равные (кратные), то мы можем получим один собственный вектор с действительными координатами.
 действительные собственные значения будут различны.
действительные собственные значения будут различны. двух векторных аргументов
двух векторных аргументов  называется билинейной формой, если она линейна по каждому аргументу, то есть
называется билинейной формой, если она линейна по каждому аргументу, то есть .
.