
|
|
Решение систем линейных уравнений методом Гаусса.Способы нахождения ранга. 1. Метод окаймляющих миноров. Сначала находят минор k– го порядка не равный 0, затем вычисляют все окаймляющие миноры (k+1). Если они равны нулю, то все миноры более высоких порядков равны нулю. Тогда r(A)=k. Если среди (k+1) – го порядка найдется минор не равный 0, надо рассматривать все (k+2) – го порядка и т.д. Пример: А= (3 r(A)
2. Метод элементарных преобразований. Опр. Элементарными преобразованиями называются следующие преобразования: 1.Транспонирование – замена строк столбцами; 2. Перестановка двух строк или двух столбцов; 3. Умножение всех элементов строки или столбца на число не равное 0; 4. Прибавление ко всем элементам строки или столбца соответствующих элементов другой строки или столбца умноженных на одно и тоже число. Теорема. При элементарных преобразованиях ранг матрицы не меняется. Если в результате элементарных преобразований получена единичная матрица вида

Если в результате элементарных преобразований получена ступенчатая (треугольная) матрица
Опр. Минор, с помощью которого устанавливается ранг матрицы, называется базисным минором. Базисных миноров может быть несколько. Пример: Найти ранг.
3 Нахождение ранга матрицы с помощью теоремы о ранге. Теорема (о ранге матрицы). Если ранг матрицы равен r, то в этой матрице можно найти r линейно независимых строк (столбцов) через которые линейно выражаются остальные ее строки (столбцы). Пример: Найти ранг.
Теорема Кронекера – Капели. Пусть дана система из m –уравнений и n – неизвестных
В частном случае если m = n и detA ≠ 0, система совместна, имеет единственное решение и оно находится матричным способом, методом Крамера или методом Гаусса. В общем случае возникает вопрос о ее совместности. Ответ на него дает теорема Кронекера – Капелли. Введем основную и расширенную матрицы системы.
- расширенная матрица.
Теорема(Кронекера – Капелли). Для совместности системы линейных алгебраических уравнений необходимо и достаточно чтобы ранг основной матрицы системы равнялся рангу расширенной матрицы Замечание:Ранг расширенной матрицы системы не может быть больше ранга основной матрицы. Согласно теореме Кронекера – Капелли если ранг основной матрицы системы меньше ранга расширенной матрицы, то система не совместна. Решение систем линейных уравнений методом Гаусса. Рассмотрим случаи для системы размерности Пусть ранг равен числу неизвестных Суть метода Гаусса состоит в том, что путем элементарных преобразований из всех уравнений системы, кроме первого, исключаем неизвестное Пример. Решить систему.
Запишем расширенную матрицу системы, поменяв местами 1 - е и 2 – е уравнение (при этом
= =
=
Матрица имеет ступенчатый вид. Основная матрица имеет размерность
Из последнего уравнения

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|

 5)
5) 3 Выберем минор , т.к. М=
3 Выберем минор , т.к. М=  тогда М=
тогда М= 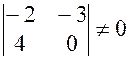 окаймляющий минор М3=
окаймляющий минор М3=  но другой М3=
но другой М3=  следовательно r(A)= 3.
следовательно r(A)= 3.
 ,то ранг равен числу не нулевых элементов на главной диагонали.
,то ранг равен числу не нулевых элементов на главной диагонали.

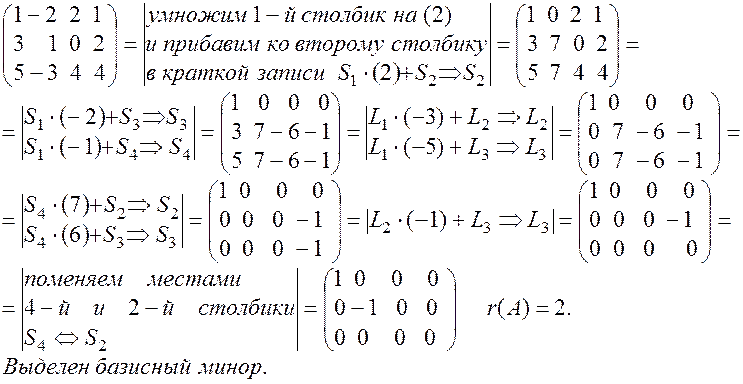
 строки данной матрицы являются линейно зависимыми так как между ними имеется следующая зависимость
строки данной матрицы являются линейно зависимыми так как между ними имеется следующая зависимость  или
или  или
или  видим, что строки
видим, что строки  - линейно выражаются через
- линейно выражаются через  . Следовательно
. Следовательно  линейно независимы и по теореме о ранге – ранг равен двум
линейно независимы и по теореме о ранге – ранг равен двум  .
. (1)
(1) - основная матрица;
- основная матрица;
 .
.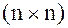 :
: . Поскольку число уравнений такой системы n равно рангу системы r, то система имеет единственное решение, которое можно найти известными методами (матричным, Крамера) или Гаусса.
. Поскольку число уравнений такой системы n равно рангу системы r, то система имеет единственное решение, которое можно найти известными методами (матричным, Крамера) или Гаусса. , далее из всех уравнений системы, кроме первого и второго, исключаем неизвестное
, далее из всех уравнений системы, кроме первого и второго, исключаем неизвестное  , и т. д.
, и т. д.
 -это значение учитывается при подсчете определителя), получим:
-это значение учитывается при подсчете определителя), получим: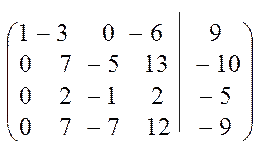

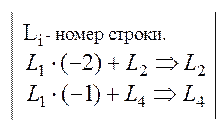

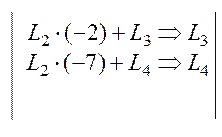

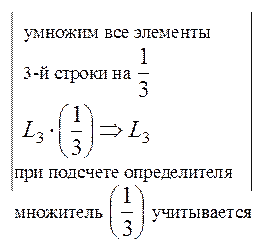




 , следовательно, ее ранг
, следовательно, ее ранг  . Расширенная матрица Размера
. Расширенная матрица Размера  ее ранг также
ее ранг также  , значит ранг основной матрицы
, значит ранг основной матрицы  . Расширенная матрица также будет иметь ранг
. Расширенная матрица также будет иметь ранг  . Обозначим
. Обозначим  Применим обратный ход метода Гаусса.
Применим обратный ход метода Гаусса. найдем
найдем  =1 и подставим в 3-е уравнение, найдем
=1 и подставим в 3-е уравнение, найдем  , получим
, получим  . Подставим
. Подставим 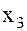 во 2-е уравнение
во 2-е уравнение  , или
, или 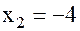 и окончательно из первого уравнения
и окончательно из первого уравнения  или
или  . Получили единственное решение системы.
. Получили единственное решение системы.