
|
|
Диаметральная плоскость поверхности второго порядка.Раздел III Общая теория поверхностей второго порядка Рассмотрим многочлен степени 2 от трех неизвестных
Инварианты общих ортогональных преобразований ПДСК в пространстве многочлена (1) Инварианты поворота и переноса
Инварианты поворота
Аффинные свойства поверхностей второго порядка. Рассмотрим поверхность второго порядка
Рассмотрим поверхность с уравнением (2) и прямую в пространстве
Рассмотрим различные случаи пересечения прямой и поверхности:
Найдем точки пересечения, т.е. решения уравнения (5) I. P=0 (5)->
Если прямая (4) удовлетворяют условию (7), то она называется прямой асимптотического направления относительно поверхности с уравнением (2). Уравнение (5), различные решения I.1. Q≠0
В этом случае прямая (4) пересекает поверхность (2) в одной точке. I.2. Q=0 R≠0 (5.1)->R=0 (противоречие) т.е. прямая не имеет точек пересечения с поверхностью, если она имеет асимптотическое направление (удовл (7)), то она является асимптотой. I.3. Q=R=0 ур-е (5)-> все точки лежащие на прямой являются точками пересечения с поверхностью, т.е. прямая (4) целиком лежит на поверхности и она называет прямолинейной образующей поверхности. Конус асимптотических направлений и асимптотический конус поверхностей. Пусть все такие прямые проходят через т. М0. Из (4)
(8) – уравнение конической поверхности второго порядка с вершиной М0. Определение. Коническая поверхность (8) называется конусом асимптотических направлений поверхности с уравнением (2). Любая прямая асимптотического направления (удовл (7)), проходящая через т.М0 лежит на этом конусе. Определение. Если т.М0 совпадает с центром поверхности второго порядка, то конус асимптотических направлений (8) называется асимптотическим конусом поверхности второго порядка.
II. P≠0 прямой неасимтотического направления относительно поверхности II.1. тогда прямая (4) пересекает поверхность в двух точках и образует хорду уравнение (5) имеет 2 корня II.2. Прямая является касательной, она касается поверхности второго порядка. II.3. Прямая не имеет точек пересечения с поверхностью второго порядка. Касательная плоскость к поверхности второго порядка Рассмотрим поподробнее случай II.2. Пусть
Для касательной прямой должно удовлетворять (*) Из (4), пусть
(*)=>
=> (**)=> Уравнению (9) должна удовлетворять любая прямая, касающаяся поверхности в т.М0. (x;y;z) – это координаты текущей точки прямой, касающейся поверхности в т.М0, т.к. это уравнение плоскости => все такие прямые укладываются в эту плоскость, она называется касательной плоскостью поверхности в т.М0.
Центр поверхности второго порядка. Центральные и нецентральные поверхности. Определение. Точка пространства называется центром поверхности второго порядка, если любая хорда поверхности, проходящая через эту точку, делится в этой точке пополам. Теорема 1.Точка М0(x0;y0;z0) – центр поверхности с уравнением (2) <=> выполняются условия
Док-во: |=> Пусть M0 – центр M1 M2 – хорда (4) и (2) M1 M0 – середина хорды M1 M2=> t1 и t2 - корни уравнения по т. Виета Q=0 (т.к.
Рассмотрим 3 линейно независимых неасимптотических вектора
Вопрос: как найти F10, F20, F30? (**) – система однородных линейных уравнений на F10, F20, F30. Рассмотрим определитель этой системы
=> по т.Крамера получаем, что
<=| Если выполняется (10), докажем, что М0 – центр. Пусть выполняется (10) для точки М0 Рассмотрим хорды, проходящие через т.M0=>Q=0=(т.Виета. ур.(5))=> => Поверхность, которая имеет единственный центр, называется центральной. (10): Пусть Тогда система (10) по теореме Крамера имеет единственное решение, поверхность имеет один центр. Если
Диаметральная плоскость поверхности второго порядка. Определение. Геометрическое место середин хорд поверхности второго порядка одного и того же неасимптотического направления {l;m;n} называется диаметральной плоскостью поверхности второго порядка, сопряженной направлению {l;m;n}. Пусть М1М2 – хорда с серединой в точке M0 =>
Рассмотрим уравнение (11) (уравнение первой степени), выделим в нем коэффициенты при x, y и z:
(11.1) Пусть
Докажем, что это уравнение первой степени методом от противного. Предположим не первой => нулевой. (13) Определение. Направление вектора Особое направление не имеет сопряженной диаметральной плоскости и является асимптотическим. Но не каждое асимптотическое направление является особым.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 (1)
(1)
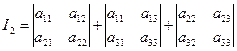

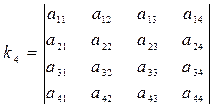


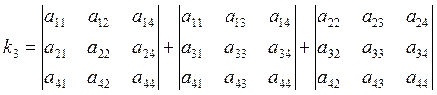
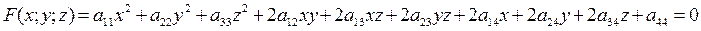 (2)
(2)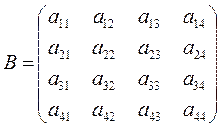
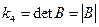
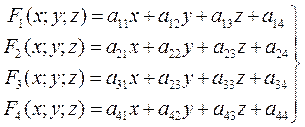 (3)
(3)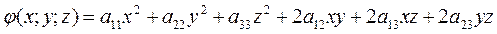

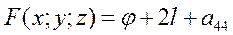
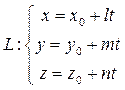 (4)
(4) 
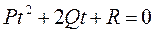 (5)
(5) (6)
(6)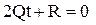 (5.1)
(5.1)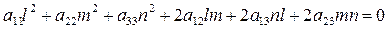 (7)
(7)
 , т.е.
, т.е.  - решение (5)
- решение (5)
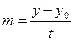
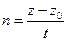 -> в (7) и делим на t2:
-> в (7) и делим на t2: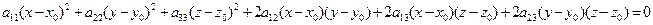 (8)
(8)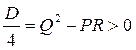
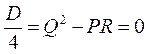

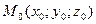 - точка касания =>
- точка касания => 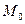 - принадлежит поверхности (2)
- принадлежит поверхности (2)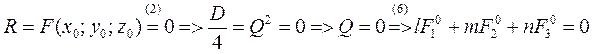 (*)
(*)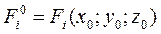
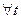
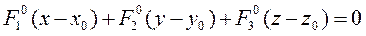 (**)
(**)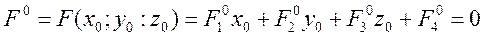
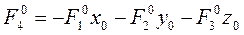
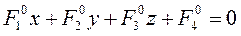 (9)
(9) ,
, 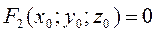 ,
, 
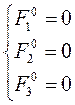 (10)
(10)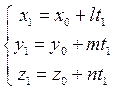 M2
M2 
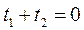
 (5)
(5)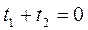 )
)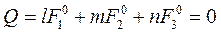 (*)
(*)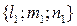 ;
;  ;
; 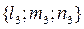 и рассмотрим хорды этих направлений, проходящие через т.M0, для них всех выполняется равенство (*)
и рассмотрим хорды этих направлений, проходящие через т.M0, для них всех выполняется равенство (*)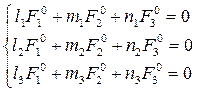 (**)
(**) , т.к. 3 вектора л/н,
, т.к. 3 вектора л/н, -- единственное решение.
-- единственное решение.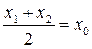 ;
; 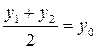 ;
;  => M0 – Центр.
=> M0 – Центр.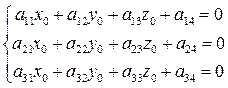

 , то поверхность является нецентральной. Такая поверхность может не иметь центра, иметь прямую центров, иметь плоскость центров.
, то поверхность является нецентральной. Такая поверхность может не иметь центра, иметь прямую центров, иметь плоскость центров.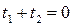 =>Q=0=>
=>Q=0=> 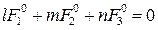 (*)
(*)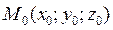 - текущая точка =>
- текущая точка => 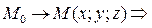 (*) превратиться в
(*) превратиться в (11) – уравнение геометрического места середин хорд.
(11) – уравнение геометрического места середин хорд.
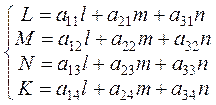 (12)
(12)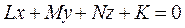 (11.1)
(11.1)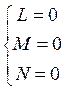 , но
, но 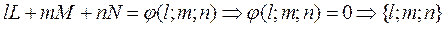 - асимптотическое направление, что противоречит условию. Следовательно, уравнение (11) – это уравнение первой степени.
- асимптотическое направление, что противоречит условию. Следовательно, уравнение (11) – это уравнение первой степени.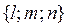 , координаты которого удовлетворяют условию (13), называется особым направлением поверхности (2).
, координаты которого удовлетворяют условию (13), называется особым направлением поверхности (2).