
|
|
Модуль 1: Линейная алгебраЛИНЕЙНАЯ АЛГЕБРА И ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ МТ, РК и ИБМ, 1 курс, 2 семестр 2011-2012 уч. г. Практические занятия Литература Основная литература (ОЛ) ОЛ-6.Сборник задач по математике для втузов. Ч. 1. Линейная алгебра и основы математического анализа: Учеб. пособие для втузов / Под ред. А.В. Ефимова, Б.П. Демидовича. – М.: Наука, 1993. – 478 с. ОЛ-8.Задачи и упражнения по математическому анализу для втузов /Под ред. Б.П. Демидовича. – М.: Астрель 2005, – 416 с. Дополнительная литература (ДЛ) ДЛ-3.Сборник задач по линейной алгебре / Под ред. С.К. Соболева. – М.: МГТУ, 1991. Методические пособия, изданные в МГТУ (МП) 1. Ильичев А.Т., Крапоткин В.Г., Савин А.С. Линейные операторы. Методические указания к выполнению типового расчета. – М.: МГТУ, 2003. – 36 с. 2. Пугачев О.В., Стась Г.П, Чередниченко А.В. Квадратичные формы и их геометрические приложения. Методические указания к выполнению типового расчета. – М.: МГТУ, 2004. – 59 с. 3. Гришина Г.В., Демин А.И., Михайлова О.В. Функции многих переменных. Методические указания к выполнению домашнего задания. – М.: МГТУ, 2003. – 44 с. 4. Богомолов В.Г., Матвеев М.В., Филиновский А.В. Дифференциальное исчисление функций нескольких переменных. – М.: МГТУ, 1993. – 52 с. 5. Богомолов В.Г., Матвеев М.В., Филиновский А.В. Прикладные задачи дифференциального исчисления функций нескольких переменных. – М.: МГТУ, 1993. – 56 с. 6. Дерябина Г.С., Чуев В.Ю. Вектор-функция нескольких переменных. – М: МГТУ, 2002, – 26 с. 7. Сидняев Н.И.. Феоктистов В.В. Линейные и евклидовы пространства. – М,: МГТУ им. Баумана, 2008. 8. Павельева Е.Б., Томашпольский В.Я. Линейная алгебра. Методические указания к выполнению типового расчета (ЭУИ). – М.: МГТУ им. Баумана, 2010. МОДУЛЬ 1: ЛИНЕЙНАЯ АЛГЕБРА Занятие 1. Линейное пространство. Линейная зависимость. Базис и размерность пространства. Переход к новому базису. Ауд.: ОЛ-6, гл. 4: 4.1–4.9 (неч.), 4.15, 4.17, 4.21, 4.24, 4.28, 4.30, 4.37 или ДЛ-3, гл. 3: 7–17 (неч.), 21–25 (неч.), 29–33 (неч.), 40, 53–57(неч.), 63. Дома: ОЛ-6, гл. 4: 4.2–4.10 (четн.), 4.16, 4.18, 4.19, 4.25, 4.31 или ДЛ-3, гл. 3: 8–14 (четн.), 22–26 (четн.), 30–34 (четн.), 42, 54–58 (четн.), 64. Занятие 2. Ранг системы векторов. Линейная оболочка системы векторов. Подпространство линейного пространства. Ауд.: ОЛ-6, гл. 4: 4.45–4.53 (неч.) или ДЛ-3, гл. 3: 73–77 (неч.), 87–91 (неч.), 95–99 (неч.). Дома: ОЛ-6, гл. 4: 4.46, 4.48, 4.52, 4.54 или ДЛ-3, гл. 3: 74–78 (четн.), 88–92 (четн.), 96–100 (четн.), гл. 4: 6–12 (четн.), 32, 38. Занятие 3. Евклидовы пространства. Процесс ортогонализации Грама – Шмидта. Ауд.: ОЛ-6, гл. 4: 4.63 (а), 4.64 (а), 4.65 (а,б), 4.67–4.76 (неч.), или ДЛ-3, гл. 4: 5–12 (неч.), 17– 24 (неч.), 31, 37, 39, 47, 49, 53, 57, 59. Дома: ОЛ-6, гл. 4: 4.63 (б), 4.64 (б), 4.65 (в), 4.67–4.76 (четн.) или ДЛ-3, гл. 4: 5–12 (четн.) 17–24 (четн.), 32, 38, 48, 50, 54, 58, 60.
Занятие 4. Линейные операторы и их матрицы. Преобразование матрицы линейного оператора при переходе к новому базису. Действия над линейными операторами. Ауд.: ОЛ-6, гл. 4: 4.83 – 4.99 (неч.), 4.103, 4.106 (б), 4.107, 4.110, 4.113 или ДЛ-3, гл. 5: 1, 5, 7, 21, 23, 25, 32 (а), 33 (а), 44, 45 (а), 47, 49, 51 (а, б), 71. Дома: ОЛ-6, гл. 4: 4.84, 4.86, 4.90 – 4.100 (четн.), 4.102, 4.104, 4.108, 4.110(б), 4.118 или ДЛ-3, гл. 5: 6, 8, 22, 24, 32 (6), 33 (б), 43, 45 (б), 48, 51 (в, г), 72. Занятие 5. Собственные векторы и собственные значения линейного оператора. Диагонализация симметричных матриц ортогональным преобразованием. Ауд.: ОЛ-6, гл. 4: 4.129, 4.131, 4.135–4.143 (неч.), 4.174, 4.183, 4.191 или ДЛ-3, гл. 5: 75–80 (неч.). 89–100 (неч.), 155–162 (неч.). Дома: ОЛ-6, гл. 4: 4.130, 4.132, 4.134–4.142 (четн.), 4.176, 4.184, 4.186 или ДЛ-3, гл. 5: 75–80 (четн). 89–100 (четн.), 156–162 (четн.). Занятие 6. Квадратичные формы, критерий Сильвестра. Преобразование матрицы квадратичной формы при переходе к новому базису. Ауд.: ОЛ-6, гл. 4: 4.218–4.225 (четн.) или ДЛ-3, гл. 6: 13, 15, 43, 45. Дома: ОЛ-6, гл. 4: 4.218–4.233 (неч.) или ДЛ-3, гл. 6: 14, 16, 44, 46. Занятия 7–8. Приведение квадратичной формы к каноническому виду методом Лагранжа и ортогональным преобразованием. Приведение кривых второго порядка к каноническому виду. Ауд.: ОЛ-6, гл. 4: 4.210, 4.211, 4.213, 4.215, 4.226, 4.228, 4.231 или ДЛ-3, гл. 6: 19, 21, 23 (б), 29, 31, 35, 47, 49, 55. Дома: ОЛ-6, гл. 4: 4.212, 4.214, 4.216, 4.227, 4.229, 4.230 или ДЛ-3, гл. 6: 20, 22, 23 (а), 30, 32, 36, 48, 50, 56. Занятие 9. Рубежный контроль по модулю 1. МОДУЛЬ 2. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ Занятие 10. Область определения ФНП. Линии и поверхности уровня. Предел и непрерывность ФНП. Ауд.: ОЛ-8: 1792 (в), 1793 (г), 1794 (в), 1795 (а), 1796 (в), 1797 (б, в), 1788 (в), найти предел на непрерывность в точке (0; 0) или ОЛ-6, гл. 7: 7.6, 7.8, 7.10, 7.19, 7.21 (построить линии и поверхности уровня), 7.32, 7.35, 7.44, 7.46, 7.50, 7.55. Дома: ОЛ-8 гл. 4: 1792 (е, и), 1793 (б, в), 1794(г, ж), 1796 (а, б), 1797 (г, е), 1799 (б) или ОЛ-6, гл. 7: 7.7, 7.9, 7.13, 7.20 (построить линии и поверхности уровня), 7.33, 7.34, 7.45, 7.47, 7.51. Занятие 11. Частные производные 1-го порядка. Частные производные высших порядков. Дифференциал первого и второго порядка ФНП. Ауд.: ОЛ-8: 1801–1825 (неч), 1892, 1894, 1897, 1834, 1838, 1844, 1917, 1924 или ОЛ-6, гл. 7: 7.57, 7.60, 7.61, 7.63, 7.66, 7.87, 7.89, 7.91, 7.103, 7.105, проверить функцию Дома: ОЛ-8: 1801–1825 (четн.), 1891, 1893, 1898, 1838, 1840, 1845, 1916, 1925 или ОЛ-6, гл. 7: 7.56, 7.58, 7.59, 7.62, 7.64, 7.67, 7.88, 7.90, 7.92, 7.102, 7.107. Занятия 12-13. Производная сложной и неявной ФНП. Производная по направлению и градиент ФНП. Касательная плоскость и нормаль к поверхности. Ауд.: ОЛ-8: 1856, 1861, 1864, 1865, 1870, 1944, 1946, 1948, 1950, 1955, 1876, 1878, 1882 (а), 1886, 1889, 1981 (а), 1982, 1985, 1986 или ОЛ-6, гл. 7: гл. 7: 7.114, 7.119, 7.122, 7.129, 7.135, 7.141, 7.145, 7.149, 7.152, 7.229 (а), 7.233 (а), 7.232, 7.234, 7.239 (а); ОЛ-6 гл. 10: 10.31–10.43 (неч.). Дома: ОЛ-8: 1857, 1862, 1863, 1871, 1943, 1947, 1949, 1956, 1877, 1879, 1882 (6), 1883, 1888, 1981 (б), 1984, 1987, 1990 или ОЛ-6, гл. 7: 7.116, 7.118, 7.123, 7.130, 7.136, 7.140, 7.146, 7.150, 7.151; 7.229 (б), 7.233 (б, в), 7.235, 7.239 (б); ОЛ-6 гл. 10: 10.32–10.44 (четн.). Занятия 14-15. Безусловный и условный экстремум ФНП. Ауд.: ОЛ-8: 2008, 2010, 2012, 2016, 2016.1, 2021–2024, 2031 или ОЛ-6, гл. 7: 7.187–7.195 (неч.), 7.201, 7.205, 7.214. Дома: ОЛ-8: 2009, 2011, 2014, 2016.2, 2023, 2024, 2033 или ОЛ-6, гл. 7: 7.187–7.195 (четн.), 7.202–7.204, 7.210–7.213. Занятие 16. Рубежный Контроль по модулю 2.
КОНТРОЛЬНЫЕ МЕРОПРИЯТИЯ (КМ) Модуль 1: Линейная алгебра КМ-1. Домашнее задание №1 «Линейная алгебра»состоит из 7 задач по темам: линейные и евклидовы пространства, линейные операторы, квадратичные формы и их геометрические приложения. Сроки выполнения: выдача– 1 неделя, прием – 7 неделя. КМ-2: Рубежный контроль № 1 по теме «Линейная алгебра», практика. Билет содержит 4-5 задач. Срок проведения – 8 неделя. КМ-3: Рубежный контроль № 1 по теме «Линейная алгебра», теория. Задание содержит 2-3 теоретических вопроса. Срок проведения – 9 неделя КМ-4. Посещаемость, поведение и прилежание в модуле 1 (недели 1–9) 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , проверить функцию
, проверить функцию 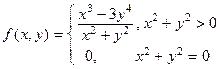
 на дифференцируемость в точке (0,0).
на дифференцируемость в точке (0,0).