
|
|
III. Аналитическая геометрия.Е.В. Бондарева
Для студентов специальностей 020400 «География», 020800 «Экология и природопользование».
Волгоград 2011 © I. Линейная алгебра Матрицы. Действия над матрицами 1. Даны матрицы: Найти: 1) А±В; 2) 5А − 7В; 3) АВ и ВА. 2. Даны матрицы: Найти: 1) 5А − 2В; 2) 2А + 3В; 3) АВ и ВА. 3. Найти произведения матриц АВ и ВА, если
5. Даны матрицы Найти произведение АВ.
6. Даны матрицы:
7. Дана матрица 8. Найти матрицу D=(AB)T − С2, если
9. Найти матрицу АВС, если
10. Вычислить А3, если 11.Даны матрицы А и В:
Найти матрицу косвенных затрат.
12. Предприятие производит продукцию трех видов и использует сырье двух типов. Нормы затрат сырья на единицу продукции каждого вида заданы матрицей § 2. Определители.
1. Вычислить определители второго порядка: 1) 2. Вычислить определители третьего порядка, используя правило треугольников: 1) 3. Вычислить определители с использованием свойств определителя: 1) 4. Вычислить определители: 1) 5) 5. Найти сумму 6. Доказать, что 7. Найти сумму 8. Найти отношение
Обратная матрица.
1.Вычислить матрицу, обратную к матрице А, если 1) 4) Сделать проверку
2. При каких значениях λ матрица А не имеет обратной 1) 3. Вычислить матрицу В = 11 · (А-1)Т + АТ , где
4.А − матрица коэффициентов прямых затрат производства
Найти матрицу коэффициентов полных затрат производства, используя формулу S = (E − А)−1
Ранг матрицы.
1.Найти ранги матриц: 1) 3)
Системы линейных уравнений. 1.Решить систему линейных уравнений методом обратной матрицы: 1) 2. Решить матричные уравнения: 1) 3) АХВ=С, если
3. Решить систему по формулам Крамера: 1) 3) 4. Решить систему методом Гаусса: 1) 3) 5) 5. Исследовать систему уравнений и решить ее в случае совместности: 1)
3)
5)
7)
9) 11) Индивидуальное задание №1 по теме: «Решение систем линейных уравнений» Решить систему уравнений: 1)Методом обратной матрицы; 2)По формулам Крамера.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
23.
24.
25.
26.
27. 20.
21.
22 II. Элементы векторной алгебры Векторы. Линейные операции над векторами (задачи на построение) 1.Даны произвольные векторы 1) 2) 3) − 2.Даны произвольные векторы 1) 2) 3) − 4) − 3. Пользуясь параллелограммом, построенном на векторах 1) ( 3) 4.Даны векторы 1) 2 2) 3 3) 4) 5. Векторы 1) | 2) | 6. Вычислить модули векторов: 1) 2) 3) 7. Найти длину вектора 8. Дан вектор 9. Дано 10. Вычислить направляющие косинусы для векторов: 1) 2) 11. Вектор
Скалярное произведение векторов. Проекция вектора на заданное направление. 1. Вычислить скалярное произведение векторов 1) 2) 3) 2. Определить угол между векторами 1) 2) 3) 3. Показать, что вектор 4. Даны координаты вершин треугольника в пространстве: А (−1; 2; 3); В (1; 1; 1); С (0; 0; 5) . Показать, что треугольник АВС – прямоугольный. 5. Найти угол между векторами А (5; −2; 3); В (7; −4; 4); С (0; −1; 2); М (4; 3; 6). 6. Определить, при каком значении m векторы 7. Даны векторы 1) 2) 8. Найти проекцию вектора 1) А (3; 1; 0); В (0; −2; 6); С (3; −2; 0); М (1; −2; 4); 2) А (− 2; 3; 4); В (2; 2; 5); С (1; −1; 2); М (3; 2; −4). Векторное произведение векторов. 1. Дано: 1) 0; 2) 30о; 3) 90о; 4) 120о; 5) 150о. 2. Упростить выражения:
3. Найти векторное произведение для следующих пар векторов:
4. Найти вектор
Вычислить в каждом случае площадь параллелограмма, построенного на векторах 5. Вычислить площадь треугольника с вершинами: 1) А (2; 2; 2); В (1; 3; 3); С(3; 4; 2); 2) А (– 3; – 2; – 4); В (– 1; – 4; – 7); С(1; – 2; 2); 6. Найти орт 1) 7. Дан треугольник с вершинами А (9; – 9; 13); В (7; – 13; 17); С(17; – 3; 17). Найти длину высоты, проведенной из вершины С. 8. Дано: 9. Дано: Смешанное произведение векторов. 1. Найти смешанное произведение векторов
2. Доказать, что векторы компланарны, если:
3. Вычислить объем тетраэдра с вершинами в точках 1) А (–1; 1; 0); В (2; – 2; 1); С(3; 1; –1); D(1; 0; –2); 2) А (–4; – 4; – 3); В (– 2; –1; 1); С(2; – 2; –1); D(– 1; 3; –2) 4. Показать, что точкиА (3; 5; – 4); В (1; –1; – 3); С(7; 2; –6); D(– 1; 3; –2) принадлежат одной плоскости. 5. Вычислить объем параллелепипеда, построенного на векторах Линейные пространства. 1. Выяснить, являются ли векторы а1, а2, а3 линейно зависимыми: 1) а1= (2; −1; 3), а2 = (1; 4; −1), а3= (0; −9; 5); 2) а1= (1; 2; 0), а2 = (3; −1; 1), а3= (0; 1; 1).
2. Показать, что векторы а1= (8; 5; 9; 1), а2 = (1; −3; –6; –3), а3= (3; –1; 5; 2), а4= (0; 2; –1; 4), заданные в базисе е1, е2, е3, сами образуют базис.
3. Даны векторы а = е1 + е2 + е3, b =2е2 + 3е3, c = е2 + 5е3, где е1, е2, е3 базис линейного пространства. Доказать, что векторы a, b, c образуют базис. Найти координаты вектора d = 2е1 − е2 + е3 в базисе a, b, c.
4. Даны векторы а1, а2, а3, b. Показать, что векторы а1, а2, а3 образуют базис трехмерного пространства, и найти координаты вектора b в этом базисе, если: 1) а1= (4; 3; 2), а2 = (−3; 2; −1), а3 = (2; 3; 1), b=(16; 8; 7); 2) а1= (−1; 2; 0), а2 = (2; 4; 2), а3 = (−3; −1; 3), b=(−8; 0; 4).
5. Даны векторы а1, а2, а3, а4, b. Показать, что векторы а1, а2, а3, а4 образуют базис четырехмерного пространства, и найти координаты вектора b в этом базисе, если: 1) а1=(–1; 2; 3; 1), а2=(–1; 3;−2; –1), а3=(3; 5; 4; 1), а4=(3;1;4;–1), b=(0; 3; 5; 4); 2) а1=(1; 2; 1; 3), а2 =(1;–1;–1;–1), а3=(–1; 3; 0;1), а4 =(1;– 2; 2;–1), b=(4; 1; 6; 0).
Индивидуальное задание №2 по теме: «Элементы векторной алгебры» Задание №1. Даны координаты вершин пирамиды ABCD. Требуется: 1. Записать векторы 2. Найти угол между векторами 3. Найти проекцию вектора 4. Найти площадь грани АВС; 5. Найти объем пирамиды АВСD.
1) А(1; 2; 1), В( – 1; 5; 1), С( – 1; 2; 7), D (1; 5; 9). 2) А(2; 3; 2), В(0; 6; 2), С(0; 3; 8), D (2; 6; 10). 3) А(0; 3; 2), В( –2; 6; 2), С( – 2; 3; 8), D (0; 6; 10). 4) А(2; 1; 2), В(0; 4; 2), С( 0; 1; 8), D (2; 4; 10). 5) А(2; 3; 0), В( 0; 6; 0), С(0; 3; 6), D (2; 6; 8). 6) А(2; 2; 1), В(0; 5; 1), С(0; 2; 7), D (2; 5; 9). 7) А(1; 3; 1), В( – 1; 6; 1), С( – 1; 3; 7), D (1; 6; 9). 8) А(1; 2; 2), В( – 1; 5; 2), С( – 1; 2; 8), D (1; 5; 10). 9) А(2; 3; 1), В(0; 6; 1), С( 0; 3; 7), D (2; 6; 9). 10) А(2; 2; 2), В(0; 5; 2), С( 0; 2; 8), D (2; 5; 10). 11) А(1; 3; 2), В( – 1; 6; 2), С( – 1; 3; 8), D (1; 6; 10). 12) А(0; 1; 2), В( – 2; 4; 2), С( – 2; 1; 8), D (0; 4; 10). 13) А(0; 3; 0), В( – 2; 6; 0), С( – 2; 3; 6), D (0; 6; 8). 14) А(2; 1; 0), В( 0; 4; 0), С( 0; 1; 6), D (2; 4; 8). 15) А(0; 2; 1), В( – 2; 5; 1), С( – 2; 2; 7), D (0; 5; 9). 16) А(1; 1; 1), В( – 1; 4; 1), С( – 1; 1; 7), D (1; 4; 9). 17) А(1; 2; 0), В( – 1; 5; 0), С( – 1; 2; 6), D (1; 5; 8). 18) А(0; 1; 0), В( – 2; 4; 0), С( – 2; 1; 6), D (0; 4; 8). 19) А(0; 1; 1), В( – 2; 4; 1), С( – 2; 1; 7), D (1; 4; 9). 20) А(0; 2; 0), В( – 2; 5; 0), С( – 2; 2; 6), D (0; 5; 8). 21) А(4; 2; 5), В(0; 7; 2), С( 0; 2; 7), D (1; 5; 0). 22) А(4; 4; 10), В(4; 10; 2), С(2; 8; 4), D (9; 6; 4). 23) А(4; 6; 5), В(6; 9; 4), С(2; 10; 10), D (7; 5; 9). 24) А(3; 5; 4), В(8; 7; 4), С(5; 10; 4), D (4; 7; 8). 25) А(10; 6; 6), В( – 2; 8; 2), С(6; 8; 9), D (7; 10; 3). 26) А(1; 8; 2), В(5; 2; 6), С(5; 7; 4), D (4; 10; 9). 27) А(6; 6; 5), В(4; 9; 5), С(4; 6; 11), D (6; 9; 3). 28) А(7; 2; 2), В(5; 7; 7), С(5; 3; 1), D (2; 3; 7). 29) А(8; 6; 4), В(10; 5; 5), С(5; 6; 8), D (8; 10; 7). 30) А(7; 7; 3), В(6; 5; 8), С(3; 5; 8), D (8; 4; 1). Задание №2 Даны векторы 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) 18) 19) 20) 21) 22) 23) 24) 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 и
и  .
. и
и 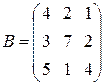 .
. и
и  .
. и
и  .
. и
и  . Доказать, что АВ ≠ ВА.
. Доказать, что АВ ≠ ВА.
 . Найти А2.
. Найти А2.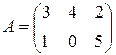 ;
;  ;
;  .
. ;
;  ;
;  .
.
 − матрица коэффициентов прямых затрат производства,
− матрица коэффициентов прямых затрат производства, −матрица коэффициентов полных затрат производства.
−матрица коэффициентов полных затрат производства. . Стоимость единицы сырья каждого типа задана матрицей
. Стоимость единицы сырья каждого типа задана матрицей  . Каковы общие затраты предприятия на производство 100 единиц продукции первого вида, 200 единиц продукции второго вида и 150 единиц продукции третьего вида? (Ответ 28 000).
. Каковы общие затраты предприятия на производство 100 единиц продукции первого вида, 200 единиц продукции второго вида и 150 единиц продукции третьего вида? (Ответ 28 000). ; 2)
; 2)  .
.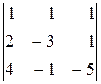 ; 2)
; 2)  .
. ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
. ;2)
;2)  ; 3)
; 3)  ; 4)
; 4)  ;
; .
. +
+  .
. = 5
= 5  .
. +
+  .
. :
: 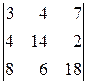 .
. ; 2)
; 2)  ; 3)
; 3)  ;
; ; 5)
; 5)  ; 6)
; 6) 
 ; 2)
; 2) 
 .
.
 ; 2)
; 2) 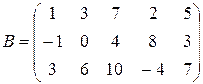 ;
; ; 4)
; 4)  .
. 2)
2) 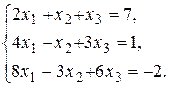
 ; 2)
; 2) 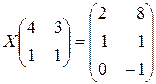 ;
; ,
,  ,
, 
 2)
2) 
 4)
4) 
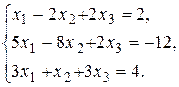 2)
2) 
 4)
4) 
 6)
6) 
 2)
2) 
 4)
4) 
 6)
6) 
 8)
8) 
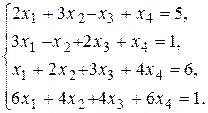 10)
10) 
 12)
12) 




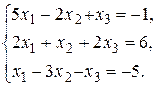
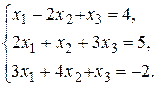











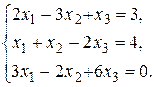
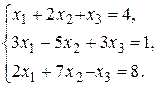





 29.
29. 
 30.
30. 
 и
и 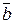 . Построить векторы:
. Построить векторы: . Построить векторы:
. Построить векторы: −
−  ;
; и
и 
 ;
;


 =5,
=5,  =12. Определить
=12. Определить − 10
− 10  + 11
+ 11 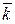 ;
; =2
=2 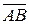 , если А (1; 2; −3) и В (3; −1; 0)
, если А (1; 2; −3) и В (3; −1; 0) = 3
= 3  и
и  , если:
, если: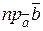 и
и  если:
если: , если угол φ между векторами равен:
, если угол φ между векторами равен: ;
2)
;
2) 
 ;
2)
;
2) 
 ;
2)
;
2)  ;
;
 ;
2)
;
2) 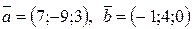 .
.
 .
.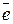 , перпендикулярный векторам:
, перпендикулярный векторам: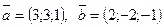 ; 2)
; 2)  ;
; =6. Найти
=6. Найти  , если:
, если: ,
, 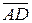 в системе орт
в системе орт 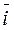 ,
,  ,
, 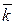 и найти модули этих векторов;
и найти модули этих векторов; ,
,  ,
,  ,
,  . Показать, что векторы
. Показать, что векторы  =(2;1;3),
=(2;1;3),  =(3; −2;1),
=(3; −2;1),  =(1; −3; −4),
=(1; −3; −4),  =(7;0;7).
=(7;0;7). =(−2; −1;2),
=(−2; −1;2),