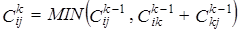Алгоритм нахождения кратчайшего пути

Неформально можно сказать, что кратчайшим путем из v_i в v_j, не проходящим через узлы, индексы которых больше k, будет более короткий из следующих двух путей:

· кратчайший путь, не проходящий через узлы, индексы которых больше k-1;

· кратчайший путь из v_i в v_k и затем в v_j, не проходящий через другие узлы, индексы которых больше k-1, то есть

Чтобы превратить алгоритм вычисления стоимости в алгоритм нахождения кратчайшего пути, зададим l(v_i, v_j) как стоимость ребра (v_i, v_j), если оно есть, и +¥ - иначе.

Теперь заменим строку 5 алгоритма последней формулой. Значение c(v_i, v_j), полученное с помощью алгоритма, будет наименьшей стоимостью, (то есть суммой стоимостей ребер) пути из всех путей между v_i и v_j.

Рис.15. Ориентированный граф

Результат работы алгоритма принято оформлять в виде совокупности таблиц, каждая из которых содержит сумму меток путей, идущих из v_i в v_j, но проходящих через вершины, индексы которых не больше чем k.

Задачи с одним источником

Во многих приложениях достаточно находить кратчайшие пути только из одного узла. Такой узел называется источником.

Работа алгоритма основана на построении множества узлов S, кратчайшие расстояния до которых от источника известны. На каждом шаге к множеству S добавляется тот из оставшихся узлов, расстояние до которого от источника меньше всех других расстояний до оставшихся узлов.

Если стоимости ребер неотрицательны, то можно быть уверенным, что путь из источника в произвольный узел проходит только через узлы из множества S. Поэтому достаточно найти для каждого узла v кратчайшее расстояние до него от источника вдоль пути, проходящего только через узлы из множества S.

Алгоритм Дейкстры

Вход. Орграф G = (V, E), источник, функция l, отображающая множество V ´ V в множество неотрицательных вещественных чисел. Полагаем l(v_i, v_j) = +¥, если ребро не принадлежит графу, v_i ¹ v_j, и l(v, v) = 0.

Выход. Для каждого узла v Î V наименьшая сумма меток на ребрах, взятая по всем путям, идущим из v₀ в v.

Метод. Строим такое множество узлов S Í V, что кратчайший путь из источника в каждый узел v Î S целиком лежит в S. Массив D[v] содержит стоимость текущего кратчайшего пути из v₀ в v, который проходит только через узлы из S.

1. S = {v₀}

2. D[v₀] = 0

3. " v Î (V \ {v₀}): D[v] = l(v₀, v)

4. S ¹ V:

5. Выбрать узел w Î (V \ S), для которого D[w] принимает наименьшее значение.

6. Добавить w к S.

7. Для v Î (V \ S):

8. D[v] = MIN(D[v], D[w] + l(w, v))

Рис.16. Граф для иллюстрации применения алгоритма Дейкстры

Результат работы алгоритма обычно оформляется в виде таблицы (табл. 1).

Таблица 1

Таблица результатов работы алгоритма Дейкстры

Метод поиска в глубину

Метод обхода узлов неориентированного графа называется поиском в глубину, так как процесс поиска идет в направлении вперед (вглубь) до тех пор, пока это возможно. Идея алгоритма состоит в следующем.

Выбираем и посещаем некоторый произвольный узел v. Затем выбираем произвольное ребро (v, w) и посещаем узел w. Пусть x – последний посещенный узел. Для продолжения процесса поиска выбираем какое-нибудь, не рассмотренное еще ребро (x, y). Если узел y уже посещался, ищем другое новое ребро, инцидентное x. Если y раньше не посещался, идем в y и заново начинаем поиск от узла y. Пройдя все пути, начинающиеся в y, возвращаемся в x, то есть в тот узел, из которого был впервые достигнут узел y. Затем продолжаем выбор нерассмотренных ребер, инцидентных узлу x, до тех пор, пока не будет исчерпан список этих ребер.

Этот метод поиска можно применить и на ориентированном графе. В этом случае, находясь в узле x, необходимо выбирать ребра (x, y), только выходящие из x. Исследовав все ребра, выходящие из y, возвращаемся в x даже тогда, когда в y входят другие ребра, еще не рассмотренные.

Метод поиска в глубину на неориентированном графе G = (V, E) разбивает множество его ребер E на два подмножества T и B. Ребро (v, w) помещается в T, если узел w не посещался до того момента, когда, рассматривая ребро (v, w), оказываемся в узле v. В противном случае, ребро (v, w) помещается во множество B.

Ребра из T называются древесными, а ребра из B – обратными. Подграф (V, T) представляет собой неориентированный лес, называемый остовным лесом для G, построенным поиском в глубину или глубинным остовным лесом для G.

Не нашли, что искали? Воспользуйтесь поиском по сайту: