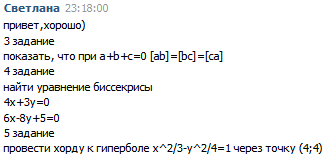у нас были 2 и 12 - одинаковые)

Билет

1)базис в пространстве, координаты вектора в базисе, векторные операции в координатах

2)уравнение при вершине параболы, эллипса и гиперболы.

3)даны 2 вектора: a{1,2,3} и b{4,5,6} найти такой вектор с, который удовлетворяет следующим условиям: a перпендикулярно с, |a|=|c|, а,b и с компланарны, угол между а и b – острый.

4)дано уравнение прямой в каноническом виде, т.е. L: (x-2)/2=(у-3)/3=(z-4)/4 и дана точка М(5,1,1), требуется найти координаты точки N на этой прямой, такой что MN-кратчайшее расстояние от M до L.

5)Дано уравнение эллипса: x^2/10 +у^2/5= 1 . Найти уравнение софокусной гиперболы. (примечание: там ещё было какое-то условие, что означает что в такой гиперболе b=a, не забудьте про него как это сделала я)

6)доказать: если в четырехугольнике суммы квадратов противоположных сторон равны, то его диагонали перпендикулярны.

16)

Точка а лежит на прямой (х-1)/2=у/3=(z+1)/1 расстоян от а до плоскости x+z+y+3=0 равно корень из 3. Найти координату а

Дана гипербола x в квадр/13-у в квад/3= 1 найти софокусный эллипс проходящий через м(4, -9/5)

Даны 3 вектора а (4,1,5) в(0,5,2) с (-6, 2,3) (x,a)=18,(xв)=1(x,c)=1 найти х

22)
1. линейная зависимость, критерий зависимости.
2. варианты уравнения плоскости
3. даны три вектора а,б,с и даны их векторные произведения, причём сумма векторов 0. доказать что векторные произведения равны
4. найти биссектрису угла между двумя линиями

7),

теория была про базис в пространстве и векторные операции а вторая уравнения элипса гиперболы и параболы отн вершины.Из практики помню 4,имеется определенная точка и рядом линия,нужно определить координаты точки на линии ближайшей к той(пересечение перпендикуляра из той точки к линии)5 задание там что то про софокусное уравнение гиперболы нужно полчуить из уравнения элипса

25)

из теории надо было вывести ур-е гиперболы,написать определение гиперболы,смешанное пр-е,из практики там задачка на линейную зависимость векторов и на пучок плоскостей...

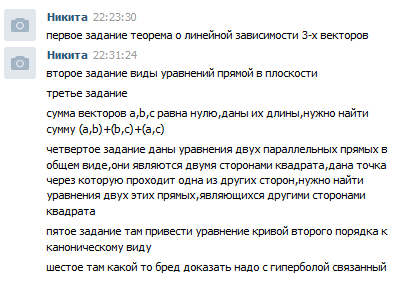
Билет

первое задание теорема о линейной зависимости 3-х векторов

второе задание виды уравнений прямой в плоскости

третье задание

сумма векторов a,b,c равна нулю,даны их длины,нужно найти сумму (a,b)+(b,c)+(a,c)

четвертое задание даны уравнения двух параллельных прямых в общем виде,они являются двумя сторонами квадрата,дана точка через которую проходит одна из других сторон,нужно найти уравнения двух этих прямых,являющихся другими сторонами квадрата

пятое задание там привести уравнение кривой второго порядка к каноническому виду

шестое там какой то бред доказать надо с гиперболой связанный

Билет №13.

1)Скалярное произведение и его свойства. Доказательство свойств. 2)перечислить уравнения прямой в пространстве. 3) заданы два вектора, на которых построен треугольник. Найти его площадь. Она равна половине модуля векторного произведения этих векторов. 4)написать уравнение плоскости, содержащей начало координат и прямую, заданную в каноническом виде. Там нужно знать способ записи ур-ия плоскости по 3-м точкам через определитель. 5)записать уравнение касательной к эллипсу, параллельной к другой заданной прямой. Надо решить систему и приравнять дискриминант к нулю. Отсюда будет найден свободный член уравнения касательной. 6) Там была странная хрень, извините за выражение, где нужно было доказать тождество, произведение векторного произведения и смешанного разных векторов равно определителю из векторов и скалярных произведений.

номер11, 1)теорема о линейной зависимости 3-х векторов 2)виды уравнений прямой 3)а+б+с=0 |a|=3 |б|=1 |c|=3 найти чему будет равно (а,б)+(б,с)+(с,а) 4)даны ур-ния 2-х прямых- стороны квадрата, нужно найти другие две(я точно ур-ния не помню) 5 и 6 я не делал поэтому не запомнил

Номер 19

был такой пример:(a,b,c)^2+|[[a,b],c]|^2=|[a,b]|^2*|c|^2 это номер три.

номер 4 чото связанно с тетраэдром плоскосятми и сферой. кажеться найти радиус сферы надо. и уравнение дано:

х+2у-2z-12=0

леммы о разложении

перевод в канонический вид уровнения кривой второго порядка

Билет №9,

1 вопрос: леммы о разложении,

2 вопрос: приведение кривой второго порядка к каноническому виду,

5 вопрос: дана прямая с параметром P и надо найти условие, при котором она коснётся заданной гиперболы, я без чисел и примеров, ибо фигню мне не нужную я не запоминаю.

4 вопрос: дано уравнение плоскости, которая отсекает от координатных осей отрезки, и образует тетраэдр, нужно найти координаты центра вписанной в него сферы и её радиус.

3 вопрос: доказать тождество: ((a,b,c)^2)+|[[a,b],c]|^2=|[a,b]|^2 * |c|^2

6 вопрос пипец какой то, я так и не понял, что там надо, да и не делал его вовсе

у нас были 2 и 12 - одинаковые)

3 задание показать, что при a+b+c=0 [ab]=[bc]=[ca]

4 задание найти уравнение биссекрисы

4x+3y=0

6x-8y+5=0

5 заданиепровести хорду к гиперболе x^2/3-y^2/4=1 через точку (4;4).