
|
|
между ними. Действительная, мнимая части, аргумент и модуль.Параметрические x = x1 +mt, y = y1 + nt, z = z1 + рt.
Через пересечение двух плоскостей. A1 x + B1 y + C1 z + D1 = 0, A2 x + B2 y + C2 z + D2 = 0;
Направляющий вектор. Направляющий вектор прямой - это любой ненулевой вектор, лежащий на данной прямой или на параллельной ей прямой. Его можно найти с помощью всех вышеперечисленных формул.
Теорема. Если в пространстве задана точка М0(х0, у0, z0), то уравнение плоскости, проходящей через точку М0 перпендикулярно вектору нормали (A, B, C) имеет вид: A(x – x0) + B(y – y0) + C(z – z0) = 0. Доказательство. Для произвольной точки М(х, у, z), принадлежащей плоскости, составим вектор . Т.к. вектор - вектор нормали, то он перпендикулярен плоскости, а, следовательно, перпендикулярен и вектору . Тогда скалярное произведение ×= 0 Таким образом, получаем уравнение плоскости Нормаль — это прямая, ортогональная (перпендикулярная) касательному пространству (касательной прямой к кривой, касательно плоскости к поверхности и т. д.)
Возможны четыре различных случая расположения двух прямых в пространстве: – прямые скрещивающиеся, т.е. не лежат в одной плоскости; – прямые пересекаются, т.е. лежат в одной плоскости и имеют одну общую точку; – прямые параллельные, т.е. лежат в одной плоскости и не пересекаются; – прямые совпадают.
Перечисленным выше случаям взаимного расположения прямых
– прямые
– прямые
– прямые
Две плоскости в пространстве могут быть либо параллельны, в частном случае совпадать друг с другом, либо пересекаться. Взаимно перпендикулярные плоскости представляют собой частный случай пересекающихся плоскостей.
Пусть плоскость
а прямая L задана каноническими уравнениями
или параметрическими уравнениями
в которых координаты направляющего вектора прямой L. Тогда: 1) если
2) если 3) если
Расстояние между точками A1 и A2 можно вычислить по формуле
Расстояние от точки до прямой — равно длине перпендикуляра, опущенного из точки на прямую. Если s= {m; n; p} - направляющий вектор прямой l, M1(x1,y1, z1) - точка лежащей на прямой, тогда расстояние от точки M0(x0, y0, z0) до прямой l можно найти, используя формулу
Расстояние между точкой и плоскостью вычисляется по следующей формуле:
где x1, y1 и z1 координаты точки, а A, B, C и D коэффициенты из общего уравнения уравнения плоскости
Угол между прямыми
Угол между плоскостями Если заданы уравнения плоскостей A1x+ B1y+ C1z + D1 = 0 и A2x + B2y+ C2z + D2 = 0, то угол между плоскостями можно найти, используя следующую формулу
Угол между прямой и плоскостью. синус угла(между прямойи плоскостьюравен косинусу угла между нормалью к плоскости и направляющим вектором прямой) между прямой, направляющий вектор которой имеет координаты
Комплексные числа. Определение. Операции. Формы записи и переход между ними. Действительная, мнимая части, аргумент и модуль. Комплексным числом называется выражение вида a + ib, где a и b – любые действительные числа, i – специальное число, которое называется мнимой единицей. Для таких выражений понятия равенства и операции сложения и умножения вводятся следующим образом:
Комплексные числа часто обозначают одной буквой, например, z = a + ib. Действительное число a называется действительной частью комплексного числа z, действительная часть обозначается a = Re z. Действительное число b называется мнимой частью комплексного числа z, мнимая часть обозначается b = Im z. Такие названия выбраны в связи со следующими особыми свойствами комплексных чисел. Модулем комплексного числа называется длина вектора, соответствующего этому числу:
Аргументом комплексного числа z = a + ib (z ≠ 0) называется величина угла между положительным направлением действительной оси и вектором Угол φ, аргумент комплексного числа, обозначается φ = arg z. Для числа z = 0 аргумент не определён.
10. Формула Муавра. Решение уравнений вида z^n = w, 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

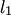 и
и 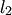 соответствуют следующие признаки:
соответствуют следующие признаки: векторы
векторы  не компланарны;
не компланарны;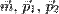 компланарны, а векторы
компланарны, а векторы  не коллинеарны;
не коллинеарны; коллинеарны, а векторы
коллинеарны, а векторы  не коллинеарны;
не коллинеарны;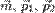 коллинеарны.
коллинеарны. задана общим уравнением
задана общим уравнением ,
,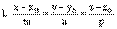
 ,
, 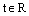 ,
, – координаты нормального вектора плоскости
– координаты нормального вектора плоскости  – координаты произвольной фиксированной точки прямой L,
– координаты произвольной фиксированной точки прямой L,  –
–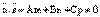 , то прямая L пересекает плоскость
, то прямая L пересекает плоскость  можно найти из системы уравнений
можно найти из системы уравнений ; (7)
; (7)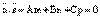 и
и  , то прямая лежит на плоскости;
, то прямая лежит на плоскости; , то прямая параллельна плоскости.
, то прямая параллельна плоскости.
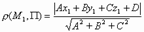
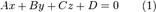

 и плоскостью, заданной уравнением
и плоскостью, заданной уравнением вычисляется по формуле:
вычисляется по формуле: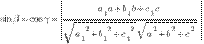

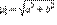
 величина угла считается положительной, если угол отсчитывается против часовой стрелки, и отрицательным в противном случае.
величина угла считается положительной, если угол отсчитывается против часовой стрелки, и отрицательным в противном случае.