
|
|
Представление перестановок в виде таблицы инверсий.Определение. Таблицей инверсий перестановки f = <a1 ... an> называется последовательность чисел r1,...,rn, где ri, 1 £ i £ n, равно числу элементов, больших i и расположенных перед ним. Таблицу инверсий будем обозначать /r1,...,rn/. Например, f = <5 1 2 6 4 7 3> r =/1,1,4,2,0,0,0/. По определению: 0 £ r1 £ n-1 0 £ r2 £ n-2 . . . 0 £ rn-1 £ 1 rn = 0. Упражнение. Пусть f = <a1 ... an>, ее таблица инверсий /r1,...,rn/. Как выглядит таблицей инверсий перестановки f=<an ... a1>? Замечание. Наряду с таблицей инверсии перестановки f можно рассмотреть таблицу r Теорема 3. Последовательность чисел r1+r Доказательство следует из определения обратной перестановки. Пусть q[i] (q`[i]), 1 £ i £ n, обозначает число элементов перестановки f, больших (меньших) i и расположенных после него. Тогда из определения также следует q[i]+r[i] = n-i q’[i]+r`[i] = i-1 q[i]+q`[i] = n-1-f-1[i] Например, f = <5 1 2 6 4 7 3> r = 1,1,4,2,0,0,0, r` = 0,1,2,2,0,3,5, q = 5,5,0,1,2,1,0, q` = 0,0,0,1,4,2,1. Следствие. Если определена какая-нибудь одна из четырех таблиц r, r`, q, q`, то из указанных соотношений легко вычисляются и три других. Упражнение. Докажите, что для заданной перестановки f, соответствующая ей таблица инверсий определяется однозначно. Указание. Воспользуйтесь следующим соотношением: пусть перестановка <a1 ... an>, (n-1) порядка соответствует /r1,...,rn-1/, тогда перестановке <a1 ... ai n аi+1 ... an> соответствует таблица инверсий /r На языке Паскаль тип данных, соответствующий таблице инверсий перестановки, может быть определен как tpi= array [1..n] of 0..n; для конкретных значений которого истинна следующая верификационная функция: function TYPEJ (var f tpi:) : Boolean; var i : 0..n; s : Boolean; begin i := n; s := true; while (i > 0) and s do begin s:=f[i] <= n-1; i := i-1 end; TYPEJ :=s end; Непосредственно из определения вытекает следующий алгоритм построения таблицы инверсий для перестановки, заданной в естественной форме: procedure TABIN (var f :TPE; var r :TPI); var i, j, k : integer; begin for i := 1 to n do begin k := f[i]; r[k] := 0; for j := i-1 downto 1 do {1} if f[j] > k then r[k] :=r[k]+1 end end; Временная сложность этого алгоритма фактически определяется числом выполнения {1}, которое равно n(n-1)/2, т. е. является О(n2). Рассмотрим теперь алгоритм восстановления перестановки в естественной форме по его таблице инверсий. Здесь возможны два похода. 1. Будем последовательно, начиная с единицы и кончая n, расставлять элементы перестановки на свои места. Вначале всем вставляемым элементам перестановки соответствуют нулевые значения. Тогда для того чтобы определить место элемента i, достаточно перед ним оставить ri нулей для элементов со значениями, большими i. Реализация этого подхода на языке Паскаль выглядит так: type P = array [1..0] of 1..n; . . . procedure TABOUT1 (var r : TPI; var f : P); var i, j, k : 0..n; begin for i := 1 to n do f[i] := 0; for i := 1 to n do begin k := r[i]+1; j := 0; repeat j := j+1; if f[j] = 0 then k :=k-1 until k = 0; f[j] := i end end; Комментарий. Для параметра f определен новый тип P, отличающийся от типа TPE тем, что его элементы массива могут получать нулевые значения. После исполнения процедуры TABOUT1 параметр f принимает значения типа TPE. Переменная k служит для пропуска нулевых значений, аj - для определения места элемента i. Упражнение. Исполните алгоритм TABOUT1 при n=5, r=/2,3,1,1,0/. Оценим временную сложность алгоритма. Она определяется числом выполнения операторов внутри цикла repeat. Пусть Ti - точное число выполнения операторов внутри цикла для заданного i. Тогда r[i]+1 £ Ti £ n. Если все перестановки из Sn равновероятны, то среднее значение r[i] равно (n-i)/2. Это приводит к тому, что вычислительная сложность этого алгоритма в среднем по всем перестановкам есть O(n2). 2. Запишем число n. Далее если r[n-1]=1, то значение n-1 поместим после n или перед ним, если r[n-1]=0. Предположим, что уже расставлены элементы n, n-1,..., i+1, тогда i нужно поставить после r[i] значений уже построенной последовательности. Например, пусть n=5, r=/2,2,1,0,0/ 1 шаг (постановка 5) r[5]=0 5 2 шаг (постановка 5) r[5]=0 4 5 3 шаг (постановка 5) r[5]=1 4 3 5 4 шаг (постановка 5) r[5]=2 4 3 2 5 5 шаг (постановка 5) r[5]=2 4 3 1 2 5 f = < 4 3 1 2 5> В реализации этого алгоритма на языке Паскаль хранение формируемой последовательности естественней всего организовать в виде линейного цепного списка. В этом случае включение в список значения i сводится к вставке в него соответствующего элемента после r[i] ранее включенных элементов. Вследствие того, что каждое значение элементов списка лежит в промежутке от 1 до n, а число элементов не превосходит n, список удобно хранить в массиве (c) из n+1 ячейки. При этом в нулевой ячейке хранится значение первого элемента списка, а в ячейке с индексом i - значение элемента следующего в списке за ним. Для последнего включенного в список элемента перестановки и для не включенных значений соответствующие ячейки равны нулю. Например, список 4®3®2®5 при n=5 будет представлен c[0]=4, c[1]=0, c[2]=5, c[3]=2, c[4]=3, c[5]=0. Реализация этого подхода на языке Паскаль выглядит так: рrocedure TABOUT2 ( var r : :TPI; var f :TPE); var c : array [0..n] of 0..n; i, j, k : 0..n; begin c[0]:=0; for i:=n downto 1 do {формирование списка} begin j:=0; for k:=r[i] downto 1do {движение по списку } {1} j:=c[j]; c[i]:=c[j]; c[j]:=i {вставка элемента } end; j:=0; for i:=1 to n do {формирование f } begin f[i]:=c[j]; j:=c[j] end end; Заметим, что временная сложность этого алгоритма определяется числом выполнения оператора {1} и равна O(n2), т. е. алгоритм TABOUT2 несколько эффективней алгоритма TABOUT1, хотя его вычислителная сложность того же порядка. Уражнение. Модернизируйте алгоритм TABOUT2 так, чтобы вспомогательный массив с совместить с массивам f. Рассмотренные TABIN и TABOUT1, TABOUT2 имеют временную сложность O(n2). Возникает естественный вопрос, существует ли алгоритм, аналогичный по действию, например, алгоритму TABIN, но имеющий лучшую временную сложность. Для того чтобы прояснить возникающие здесь проблемы, рассмотрим близкие к исследуемым понятия, связанные с алгоритмами линейного упорядочивания значений элементов (сортировки). Пусть задан некоторый массив X, например, X : array [1..n] of real; При этом для упрощения рассуждений будем считать, что все значения элементов Х различны между собой. Тогда задача упорядочивания (например в порядке возрастания значений) может быть интерпретирована как поиск перестановки f = <a1 … an>, где ak – порядковый номер элемента X[k] после упорядочивания, 1£k£n. Для любого элемента X[k] можно определить следующие числа: b[k] (b`[k]) – число элементов Х, больших (меньших) X[k] и расположенных перед ним; c[k] (c`[k]) – число элементов Х, больших (меньших) X[k] и расположенных после него; Например, X = -2.5 1.3 1.0 -0.8 0.3 -5.0 f = <2 6 5 3 4 1> b = 0 0 1 2 2 5 b`= 0 1 1 1 2 0 c = 4 0 0 1 0 0 c`= 1 4 3 1 1 0 Нетрудно показать, что для любого k, 1£k£n, определены следующие соотношения: (1) b`{k} + c`[k] + 1 = f[k] (2) b{k} + c[k] + 1 = n-f[k] (3) b{k} + b`[k] + 1 = k (4) c{k} + c`[k] + 1 = n-k Из соотношений (3), (4) следует: если по массиву Х определены таблицы b, c, то легко вычислить таблицы b`, c`, и обратно. Из соотношений (1), (2) следует: если вычислены b` и c` (либо b и c), то легко построить таблицу f. По характеру своего числа b, b`, c, c` весьма близки к числам r, r`, q, q`, определенным для перестановок. Рассмотрим вопрос, какова может быть временная сложность при вычислении по массиву Х таблиц, например, b`и c`? Пусть A(b`,c`) – временная сложность наиболее эффективных алгоритмов вычисления b` и c`, а A(f) – временная сложность наиболее эффективных алгоритмов вычисления f; тогда, так как f линейно зависит от b` и c`, то A(b`,c`)/ A(f) =O(1). Из теории сортировки известно, что если не задана дополнительная информация о структуре значений элементов массива, то наиболее эффективные алгоритмы сортировки имеют временную сложность O(n×log2n). Это следует, например, из следующих рассуждений. В зависимости от исходных значений элементов Х ему может соответствовать любая из n! Возможных перестановок f. Фактически алгоритм сортировки может быть интерпретирован как поиск соответствующей ему перестановки f из множестваSn, элементы которого упорядочены некоторым образом. Но наиболее эффективный алгоритм поиска индекса элемента в упорядоченном массиве размерностью k – это бинарный поиск, временная сложность которого O(log2k). То есть поиск конкретной перестановки из n! упорядоченных перестановок оценивается минимальной временной сложностью O(log2n!). Упражнение. Докажите равенство O(log2n!) = O(n×log2n).Указание. Воспользуйтесь неравенством n×ln(n)-n+1 < ln(n!) < (n+1)×ln(n)-n+1, n>1, которое доказывается индукцией по n. Таким образом, для произвольного массива Х наиболее эффективные алгоритмы вычисления таблиц b` и c` не могут иметь временную сложность лучшую, чем O(n×log2n). Возвратимся к алгоритмам построения таблицы инверсий для заданной перестановке f. Приведенные рассуждения наводят на мысль поиска подобного алгоритма сложностью O(n×log2n). Действительно, такой алгоритм существует. Однако его построение требует привлечение новых идей, которые в данных методических указаниях не рассматривались. Можно показать, что алгоритмы с временной сложностью O(n×log2n) являются наиболее эффективными алгоритмами построения таблицы инверсий. Такое доказательство строится на построении модели, в которой инверсиям соотвествуют некоторые операции, и эту модель характеризуют O(n!) состояний. Однако этот материал явно выходит за рамки данных методических указаний.
Перейдем к рассмотрению алгоритмов выполнения операций суперпозиции, вычисления обратной и четности для перестановок, заданных в виде таблицы инверсий. Наиболее простой из них – определение четности перестановки. В самом деле, непосредственно из определения таблицы инверсий следует, что перестановка четна, если сумма всех ее элементов таблицы инверсий четна, и нечетна в противном случае. Упражнение. Напишите булевскую функцию с заголовком function Ч3 (var r :TPI) : Boolean; и временной сложностью O(n), определяющую четность перестановки, заданной в виде таблицы инверсий. Рассмотрим алгоритм определения таблицы инверсий обратной перестановки для перестановки, заданной в виде таблицы инверсий. Теорема 4. Для любой перестановки fÎSn, число инверсий f совпадает с числом инверсий f-1. Доказательство. Пусть f = <a1 … an>, f-1 = <b1 … bn> и х = /x1,...,xn/, y = /y1,...,yn/ - таблицы инверсий f и f-1 соответственно. Рассмотрим элемент i, 1 £ i £ n, d перестановке f, расположенный на k-м месте; и пусть j Тогда в перестановке f-1 на i-м месте располагается элемент k и он образует инверсии с элементами k Аналогично доказывается, что каждой инверсии перестановки f-1 однозначно сопоставляется инверсия перестановки f. Приведенное доказательство может быть наглядно представлено следующим образом. Рассмотрим таблицу размером n´n. Поставим ‘·’ в k-й клетке i-й строки. После этого расставим символ ‘1’ в позициях k
Пример. Матрица инверсий заданной перестановки f = <2 7 3 6 5 1 4>, f-1 = <6 1 3 7 5 4 2> x = /5,0,1,3,2,1,0/, y = /1,5,1,3,2,0,0/.
Алгоритм вычисления y по x с использованием рассмотренных идей на языке Паскаль может выглядеть так: procedure O3 (var x,y : TPI); var k, i, j, s, : integer; next : array [0..n] of integer; begin for i:=1 to n do begin y[i]:=0; next [i]:=i+1 end; next [0]:=1; {3} for i:=1 to n-1 do {2} begin s:=0; k:=next[0]; j:=x[i]; while j>0 do begin y[k]:=y[k]+1; {1} s:=k; k:=next[k]; j:=j-1 end; next[s]:=next[k] {4} end end; Комментарий. Для каждого столбца k матрицы инверсий алгоритм последовательно подсчитывает число единиц, расположенных в этом столбце. Перебор строк матрицы организован циклом {2}, а столбцов – с помощью вспомогательного массива next и ограничен числом инверсий в текущей строке. Для исключения столбцов, в которых ‘·’ расположена текущей строки, осуществляется корректировка значений массива next. В начальный момент всем значениям элементов массива next присваивается ссылка на следующий элемент {3}, а при достижении точки в данной строке ссылка на текущий столбец исключается из списка (оператор {4}). Переменные s и k хранят значения индексов предыдущего и текущего столбца соответственно. Временная сложность алгоритма O3 оценивается числом выполнения оператора {1}, равного числу инверсий перестановки f. Ее порядок O(n2). Упражнение. Протестируйте алгоритм O3 на перестановки, рассмотренной в предыдущем примере. Рассмотрим алгоритм вычисления суперпозиции двух перестановок, в случае если они представлены в виде таблицы инверсий. Один из подходов может состоять в преобразовании перестановок, например, в естественную форму, затем в выполнении суперпозиции и обратного преобразования результата. Упражнение. Напишите процедуру на языке Паскаль, реализующую вычисление суперпозиции перестановок по указанной схеме, с использованием ранее рассмотренных процедур для преобразований и вычисления суперпозиции перестановок в естественной форме. Подобная схема алгоритма имеет временную сложность O(n2). Улучшенные варианты этой схемы реализации (за счет более эффективных схем перевода из одной формы в другие) имеют временную сложность O(n×log2n). В качестве упражнения, являющегося скорее исследованием, предлагается ответить на следующие вопросы. Существует ли более эффективная реализация алгоритма суперпозиции для перестановок, представленных в виде таблиц инверсий? Можно ли, ‘непосредственно’ преобразуя исходные таблицы исходных данных, получить таблицу результата? В этой теме были рассмотрены представления перестановок: в естественной форме, разложением на циклы (с разметкой начала циклов и каноническое) и таблицей инверсий. Над перестановками рассматривались операции суперпозиции, вычисления обратной и определения четности. В зависимости от внутреннего представления, выполнение этих операций существенно различно и имеет различные характеристики временной сложности. Однако с точки зрения пользователя (например, алгебраиста, решающего на ЭВМ свою конкретную задачу, описанную в терминах этих операций) совершенно безразлично, в каком представлении будут выполняться эти операции. Для него перестановки выступают как некоторый абстрактный тип данных, характеризующийся только тем, что отличает одну перестановку от другой, и возможностью выполнения указанных операций. Такое выделение понятия абстрактного типа данных методически весьма оправдано – оно позволяет пользователю описывать решение своей задачи в наиболее естественной и удобной форме, а проблему внутреннего представления этих типов данных либо оставить на более позднее время, либо передать другому специалисту, лучше знакомому с представлением данных на ЭВМ. Кроме построенного абстрактного типа данных, на множестве всех перестановок можно построить другой тип, определив иные выполняемые операции. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ,...,r
,...,r 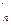 антиинверсий перестановки f, где r
антиинверсий перестановки f, где r  определяется как число элементов f, меньших i и расположенных перед ним.
определяется как число элементов f, меньших i и расположенных перед ним. +1,..., rn+r
+1,..., rn+r  ,0/, где r
,0/, где r  =rk, если kÎ{a1 ... ai} и r
=rk, если kÎ{a1 ... ai} и r  ,…, j
,…, j  - элементы в f, которыми i образуют инверсию, и расположенные левее i. Индексы элементов j
- элементы в f, которыми i образуют инверсию, и расположенные левее i. Индексы элементов j 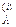 ,…, k
,…, k 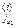 . Заметим, что j
. Заметим, что j 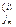 <k, 1£m£xi
<k, 1£m£xi ,i) перестановки f однозначно сопоставляется инверсия (k, k
,i) перестановки f однозначно сопоставляется инверсия (k, k