
|
|
Каждый граф укладывается в R3.Доказательство При доказательстве упомянутой формулы Эйлер использовал технику двойного (повторного) счёта. Он посчитал количество инцидентных пар (v,e), где e — ребро и v — одна из его концевых вершин двумя разными способами. Вершина v принадлежит парам deg(v), где deg(v) — степень вершины (количество инцидентных ей рёбер). Следовательно, число инцидентных пар совпадает с суммой всех степеней. Однако каждое ребро принадлежит двум инцидентным парам, так как имеет две концевые вершины. Поэтому число инцидентных пар равно 2|E|. Поскольку две данные формулы предназначены для одного и то же множества, их значения одинаковы. Чётность или нечётность суммы целых чисел не зависит от количества чётных слагаемых. Сумма чётна, если число нечётных слагаемых чётно (и нечётна в противном случае). Так как одна часть уравнения всегда чётна (2|E|), другая часть должна содержать чётное число нечётных слагаемых, т. е. вершин нечётной степени.
Число вершин нечетной степени в любом графе четно.
Доказательство Пусть дан (n,m) – граф G. Составим сумму степеней всех его вершин. где Так как первое слагаемое – четное число, то равенство примет вид Отсюда
Изоморфизм На рисунке изображены два графа с одним и тем же множеством вершин Графы Тот факт, что графы Для графов, изображенных на рисунке, изоморфизмом является, например, отображение, задаваемое следующей таблицей:
Заметим, что в этом примере есть и другие изоморфизмы первого графа на второй. Сформулированное определение изоморфизма годится и для ориентированных графов, нужно только обе упоминаемые в нем пары вершин считать упорядоченными. Изоморфизм - бинарное отношение на множестве графов. Очевидно, что это отношение рефлексивно, симметрично и транзитивно, то есть является отношением эквивалентности. Классы эквивалентности называются абстрактными графами. Когда говорят, что рассматриваются абстрактные графы, это означает, что изоморфные графы считаются одинаковыми. Абстрактный граф можно представлять себе как граф, у которого стерты имена (пометки) вершин, поэтому абстрактные графы иногда называют также непомеченными графами.
Геометрическая реализация — фигура, вершинам которой соответствуют вершины графа, рёбрам — рёбра графа и рёбра в фигуре соединяют вершины, соответствующие вершинам в графе. Укладка графа - отображение вершин и ребер графа соответственно в точки и непрерывные кривые некоторого пространства такое, что вершины, инцидентные ребру, отображаются в концы кривой, соответствующей этому ребру. Правильной укладкой наз. укладка, при которой разным вершинам соответствуют различные точки, а кривые, соответствующие ребрам (исключая их концевые точки), не проходят через точки, соответствующие вершинам, и не пересекаются. Любой граф допускает правильную укладку в трехмерное пространство. Каждый граф укладывается в R3. Все вершины произвольного графа G помещаем в различных точках координатной оси х. Рассмотрим пучок плоскостей, проходящих через ось х, и зафиксируем |E| различных таких плоскостей. Теперь каждое ребро (u, v) изобразим полуокружностью, проходящей в соответствующей плоскости через вершины u, v. Ясно, что различные ребра не будут пересекаться кроме как в общих вершинах.
Геометрический граф назовем плоским графом, если он нарисован на плоскости так, что все линии, изображающие его ребра, пересекаются только в точках, соответствующих вершинам графа, т.е. любая точка пересечения таких линий есть вершина, инцидентная ребрам, которые эти линии изображают. Любой граф, изоморфный плоскому графу, называют планарным. О планарных графах говорят, что они укладываются на плоскости (имеют плоскую укладку). Планарный граф можно уложить на плоскости, а плоский граф - это граф, уже уложенный на плоскости. Плоский граф есть изображение планарного графа, однако не каждое изображение планарного графа является плоским графом.
3. Пустой граф (вполне несвязный граф, нуль-граф) — регулярный граф степени 0, то есть граф, не содержащий рёбер. Полный граф— граф, в котором для каждой пары вершин Произведения графов a) Декартовым произведением G1□G2 называется граф G, для которого V(G)= V1xV2 – декартово произведение множеств вершин исходных графов, а E(G) определяется следующим образом: вершины (и1, u2) и (v1, v2) смежны в графе G тогда и только тогда, когда или и1=v1, а u2 и v2 смежны в G2, или и2=v2, а u1 и v1 смежны в G1. b) Категорийным произведением G1xG2 называется граф G, для которого V(G)= V1xV2 – декартово произведение множеств вершин исходных графов, а E(G) определяется следующим образом: вершины (и1, u2) и (v1, v2) смежны в графе G тогда и только тогда, когда u1 и v1 смежны в G1 и u2 и v2 смежны в G2. c) Сильным произведением G1 x G2 называется граф G, для которого V(G)= V1xV2 – декартово произведение множеств вершин исходных графов, а E(G) определяется следующим образом: вершины (и1, u2) и (v1, v2) смежны в графе G тогда и только тогда, когда u1 и v1 смежны в G1, а u2 и v2 смежны в G2 или и2=v2, или u2 и v2 смежны в G2, а u1 и v1 смежны в G1 или и1=v1. Примеры:
Предположим, что G является неориентированным графом. В качестве маршрута графа G={V,E}, V={a1, a2, ...,an}, E={l12=(a1, a2),…,lk-1 k=(ak-1, ak)} определяют такую очередность ребер M={l12,l23,…,lk-1 k}, что для двух соседних ребер характерна общая инцидентная вершина, a1 есть начальная, an- конечная вершины. Под длиной маршрута понимают количество ребер маршрута. Маршрут M именуют цепью в случае, когда все его ребра различны. Простой цепью маршрут M можно назвать, если все его вершины, за исключением первой и последней, различны. Так, для графа, изображенного на рис. 1 обозначим: abdbe - маршрут, а не цепь, abcdbe представляет собой непростую цепь, abe является простой цепью. Цепь, которая предполагает совпадение начальной и конечной вершин, имеет название цикла, в случае, когда цепь простая, — простого цикла.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ,
, – множества четных и нечетных натуральных чисел соответственно.
– множества четных и нечетных натуральных чисел соответственно. .
. , т. е. сумма всех нечетных степеней графа – четное число. Сумма нечетных чисел может быть четна тогда и только тогда, когда число слагаемых этой суммы четно, следовательно, число вершин нечетной степени четно.
, т. е. сумма всех нечетных степеней графа – четное число. Сумма нечетных чисел может быть четна тогда и только тогда, когда число слагаемых этой суммы четно, следовательно, число вершин нечетной степени четно. . При внимательном рассмотрении можно обнаружить, что это разные графы - в левом имеется ребро
. При внимательном рассмотрении можно обнаружить, что это разные графы - в левом имеется ребро  , в правом же такого нет. В то же время, если не обращать внимания на наименования вершин, то эти графы явно одинаково устроены: каждый из них - цикл из четырех вершин. Во многих случаях при исследовании строения графов имена или номера вершин не играют роли, и такие графы, один из которых получается из другого переименованием вершин, удобнее было бы считать одинаковыми. Для того чтобы это можно было делать "на законном основании", вводится понятие изоморфизма графов.
, в правом же такого нет. В то же время, если не обращать внимания на наименования вершин, то эти графы явно одинаково устроены: каждый из них - цикл из четырех вершин. Во многих случаях при исследовании строения графов имена или номера вершин не играют роли, и такие графы, один из которых получается из другого переименованием вершин, удобнее было бы считать одинаковыми. Для того чтобы это можно было делать "на законном основании", вводится понятие изоморфизма графов. 
 и
и  называются изоморфными, если существует такая биекция
называются изоморфными, если существует такая биекция  множества
множества  на множество
на множество  , что
, что  тогда и только тогда, когда
тогда и только тогда, когда  . Отображение
. Отображение  .
. (вершина графа
(вершина графа  )
)



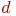
 (вершина графа
(вершина графа  )
)

 Пример плоского графа приведен на рис. 4.12. Изоморфный ему полный граф
Пример плоского графа приведен на рис. 4.12. Изоморфный ему полный граф  (рис.4.13), укладываемый на плоскости, имеет два пересекающихся ребра, поэтому граф
(рис.4.13), укладываемый на плоскости, имеет два пересекающихся ребра, поэтому граф  Существуют и непланарные графы. На рисунке показаны два таких графа: полный пятивершинник и полный двудольный граф. Для них есть специальные обозначения: K5 и K3,3 соответственно.
Существуют и непланарные графы. На рисунке показаны два таких графа: полный пятивершинник и полный двудольный граф. Для них есть специальные обозначения: K5 и K3,3 соответственно. , существует ребро, инцидентное
, существует ребро, инцидентное  и инцидентное
и инцидентное  (каждая вершина соединена ребром с любой другой вершиной).
(каждая вершина соединена ребром с любой другой вершиной).




