
|
|
В12. Прямая на плоскости (плоскость) как линия (поверхность) первого порядка. Геометрический смысл коэффициентов общего ур-я прямой на плоскости (плоскости) в ДПСК.В1. Понятие вектора. Линейные операции над векторами и их св-ва. Вектором наз направл отрезок или упорядоч пара точек пространства,плоскости,прямой. ( Длиной(модулем,абсолют величиной вект) наз расстояние между началом и концом. | Ненулевые векторы Два ненулевых вектора a и b наз равными , если : 1. | 2. 3. Свободным вектором наз любой представитель из равных между собой геометр векторов Суммой векторов Разностью Если векторы Произведением вектора 1) 2) Очевидно, что при α=0 Вектор Свойства линейных операций: 1) 2) 3) 4) для любого 5) α( 6) (α+β) 7) 8) 1 Пусть # 1) a) Сущ б) Сущ
В2. Линейная зависимость и Линейная независимость векторов. Достаточные условия линейной зависимости. Критерий линейной зависимости.
В3. Теоремы о линейной зависимости 2-х, 3-х, 4-х векторов.
В4. Определение базиса на плоскости и в пространстве. Теорема о единственности разложения вектора по базису.Координаты вектора и их св-ва. Теоремы о базисе в пространстве , на прямой , на плоскости.
В5. Угол между векторами. Проекция вектора на ось. Св-ва проекции вектора на ось.
В6. Скалярное произведение векторов, его св-ва, выражение через координаты перемножаемых векторов. Условие ортогональности двух векторов.
Условие ортогональности двух векторов:
Т.о., для того чтобы два вектора были перпендикулярны необходимо и достаточно, чтобы сумма произведений соответствующих координат этих векторов была равна нулю.
В7. Векторное произведение векторов,его св-ва, выражение через координаты перемножаемых векторов. Условие коллинеарности двух векторов.
Теорема. Если 2 вектора а и b определены своими декартовыми прямоугольными координатами а={X1,Y1,Z1} , b={X2,Y2,Z2} , то векторное произведение этих векторов имеет вид [ab]={Y1Z2-Y2Z1,Z1X2-Z2X1,X1Y2-X2Y1} или [ab]= # Составим из тройки базисных веторов i,j,k все возможные пары и для каждой из пар подсчитаем векторное произведение. Учитывая, что базисные векторы взаимно ортогональны,образают правую тройку и имеют единичную длину. [ii] = 0 [ji] = -k [ki] = j [ij] = k [jj] = 0 [kj] = -i [ik] = -j [jk] = i [kk] = 0 [ab]=X1X2[ii]+X1Y2[ij]+X1Z2[ik]+Y1X2[ji]+Y1Y2[jj]+Y1Z2[jk]+Z1X2[ki]+Z1Y2[kj]+Z1Z2[kk] [ab]=(Y1Z2-Y2Z1)i+(Z1X2-Z2X1)j+(X1Y2-X2Y1)k #Следстиве. Если 2 ветора коллинеарны, то их координаты пропорциональны(x1/x2=y1/y2=z1/z2) Условие коллинеарности двух векторов. Если ненулевые векторы
В8. Смешанное произведение, его св-ва, выражение через координаты перемножаемых векторов. Условие компланарности 3 векторов.
Теорема. Если 3 вектора a, b и c определены своими декартовыми прямоугольными координатами а={X1,Y1,Z1} , b={X2,Y2,Z2} , c={X3,Y3,Z3} , то смешанное произведение abc равняется определителю, строки которого соответственно равны координатам перемножаемых векторов, т.е. [abc]= # Т.к. смешанное произведение abc равно скалярному произведению векторов [ab] и с , получим abc = X3(Y1Z2-Y2Z1)+Y3(Z1X2-Z2X1)+Z3(X1Y2-X2Y1) или abc = X3 # Следствие. Необходимым и достаточным условием компланарности 3 векторов a,b и с является равенство нулю определителя.
В9. Афинные и декартовы системы координат на плоскости и в пространстве, координаты точки. Преобразования декартовых прямоугольных на плоскости.
В10. Алгебраические линии и поверхности. Теорема об инвариантности порядка линии при переходе от одной ДПСК к другой.
При переходе от одной ДПСК к другой порядок поверхности не меняется.
В11. Ур-е прямой на плоскости и плоскости в пространстве, проходящих через заданную точку перпендикулярно заданному вектору.
В12. Прямая на плоскости (плоскость) как линия (поверхность) первого порядка. Геометрический смысл коэффициентов общего ур-я прямой на плоскости (плоскости) в ДПСК.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 или
или  )
) |=0
|=0 наз коллинеарными
наз коллинеарными  , соединяющий начало вектора
, соединяющий начало вектора  Û
Û  .
. называется вектор
называется вектор  ), определяемый следующими условиями:
), определяемый следующими условиями: ,
, при
при  и
и 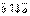 при
при  .
. .
.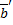 противоположен вектору
противоположен вектору 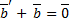 ,
,  +
+  =
= 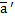 :
:  +
+ 
 =
=  +
+ 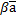
 ) =
) =  )
) и
и  ,α=0 2)
,α=0 2)  ,
,











 или
или  .
.


 .
. =(
=(  ,
, 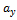 ,
,  ) и
) и  =(
=(  ,
,  ,
,  ) коллинеарны, то по определению векторного произведения
) коллинеарны, то по определению векторного произведения  =
=  , что равносильно равенству
, что равносильно равенству  =
= 

 .
. -Y3
-Y3  +Z3
+Z3 
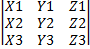 = 0.
= 0.




