
|
|
Свойства умножения вектора на число.12 1) 2) 3) 4)
Доказательство 1). Пусть для простоты
Рис.3. Иллюстрация свойства сложения векторов Доказательство 2)–4). Очевидно, и при этом получаются коллинеарные вектора. Теорема 1. Множество векторов пространства образует линейное пространство. Доказательство. Следует из свойств сложения векторов и умножения на число.∎ Замечание. Можно определить операцию вычитания векторов по формуле
Рис. 4. Вычитание векторов a) Множество коллинеарных векторов образует линейное пространство б) Множество компланарных векторов образует линейное пространство. Далее выясним размерности и базисы перечисленных пространств. 2о. Размерность линейных пространств геометрических векторов. Теорема 2. Два вектора коллинеарны тогда и только тогда, когда они линейно зависимы. Доказательство. Если один из векторов нулевой, то очевидно. Поэтому далее предполагаем, что оба вектора ненулевые.
Следствие 1. Линейное пространство коллинеарных векторов одномерно и его базисом может служить любой ненулевой вектор. Следствие 2. Если Доказательство. Теорема 3. Три вектора компланарны тогда и только тогда, когда они линейно зависимы. Доказательство. Будем предполагать, что никакие два вектора из трех не коллинеарны, так как иначе утверждение очевидно в силу свойства линейно зависимых векторов.
Рис.5. Иллюстрация доказательства теоремы 4.
Следствие. Линейное пространство компланарных векторов двумерно и его базисом может служить любая пара неколлинеарных векторов. Теорема 4. Любые четыре вектора линейно зависимы. Доказательство. Предположим, что никакие три из векторов
Рис.6. Иллюстрация доказательства 5. Следствие. Линейное пространство всех геометрических векторов трехмерное. Его базисом могут служить любые три некомпланарных вектора. 3о. Проекции вектора на ось Пусть в пространстве задана некоторая прямая l и вектор Определение 11.Осью l будем называть прямую, на которой задано направление. Направление оси задается вектором
Рис.7. Проекция точки А на ось l.
Пусть Если наряду с точкой Определение 12.Так построенный вектор Иногда говорят, что Вектора Определение 13.Такое число Таким образом Легко видеть, что Свойства проекции. 10. Проекция вектора на ось равна произведению длины вектора
Рис.8. Действительно, пусть Если
Если
20. При умножении вектора на число его проекция на ось также умножается на это число: Действительно, если Если
30. Проекция суммы векторов на ось равна сумме проекций слагаемых:
Справедливость этого утверждения следует из рис.9. В случае а)
а) б) Рис.9. Иллюстрация доказательства свойства о проекции суммы векторов. Следствие. Свойство (3) справедливо для " количества векторов.
40.Скалярное произведение векторов. Определение 14.Скалярным произведением двух векторов Таким образом, если

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 и
и 

 .
.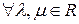 и
и  вектора
вектора 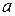
 .
.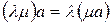 .
. .
. и будем использовать правило параллелограмма для сложения векторов. Если вместо
и будем использовать правило параллелограмма для сложения векторов. Если вместо  взять
взять  и
и 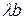 , то получим подобный параллелограмм и его диагональ соответственно равна
, то получим подобный параллелограмм и его диагональ соответственно равна 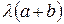 (см. рис.3).
(см. рис.3).

 (см. рис.4)
(см. рис.4)
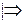 Пусть
Пусть 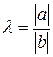 . Тогда если
. Тогда если  , то
, то 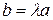 , если
, если  , то
, то  . В обоих случаях
. В обоих случаях  Пусть
Пусть  , где
, где  не равно 0. Тогда, если
не равно 0. Тогда, если  ,
, 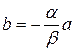
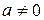 , то
, то  R:
R: 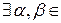 R:
R: 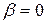
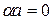
 . Т.о.
. Т.о. 
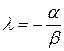 .
. компланарны. Перенесем их в точку O, проведем через конец вектора c прямые, параллельные векторам
компланарны. Перенесем их в точку O, проведем через конец вектора c прямые, параллельные векторам  .(см. рис. 5) Векторы
.(см. рис. 5) Векторы  ,
, 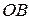 – коллинеарны
– коллинеарны  R:
R: 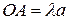 ,
,  . Но
. Но 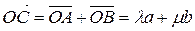
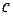 ,
, 
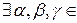 R, одновременно не равные нулю:
R, одновременно не равные нулю:  . Если, например,
. Если, например,  , то
, то 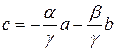
 не компланарны (иначе они линейно зависимы) очевидно. Остальное следует из (рис.6) по аналогии с доказательством теоремы 4. Через точку D проведем три плоскости, параллельные парам векторов {
не компланарны (иначе они линейно зависимы) очевидно. Остальное следует из (рис.6) по аналогии с доказательством теоремы 4. Через точку D проведем три плоскости, параллельные парам векторов { 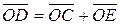 ,
, 
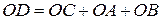 .
. 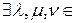 R:
R: 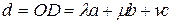
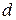 – линейно зависимы.∎
– линейно зависимы.∎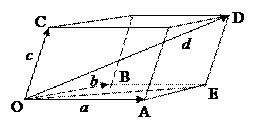
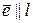 .
.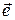 (направляющий вектор оси).
(направляющий вектор оси).

 – точка, не принадлежащая l. Проведем через точку
– точка, не принадлежащая l. Проведем через точку 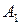 , которая называется проекцией (ортогональной проекцией) точки
, которая называется проекцией (ортогональной проекцией) точки 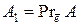 (см. рис.7).
(см. рис.7). .
. называется векторной проекцией вектора
называется векторной проекцией вектора  на ось l. Обозначают:
на ось l. Обозначают:  .
. – коллинеарны Þ
– коллинеарны Þ 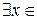 R:
R:  .
. называется скалярной проекцией (проекцией) вектора
называется скалярной проекцией (проекцией) вектора  или
или  .
. .
.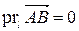 Û
Û 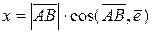 .
.
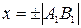 - проекция вектора
- проекция вектора  , б)
, б) 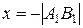
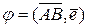 .
. (см. рис. 8а), то
(см. рис. 8а), то 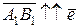 , поэтому
, поэтому .
. (см. рис. 8б), то
(см. рис. 8б), то  , и
, и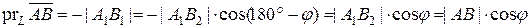 .
. .
. и
и 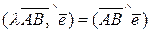 l и
l и  .
. , то
, то 


 .
.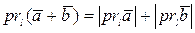 , б)
, б) 






 и
и  называется число, равное произведению длин этих векторов на косинус угла между ними.
называется число, равное произведению длин этих векторов на косинус угла между ними. и
и .
.