
|
|
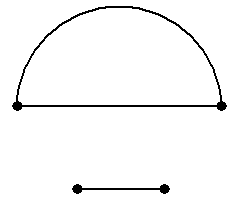
Внутренне- и внешне устойчивые множества вершинДадим определения сразу для неориентированного и ориентированного случаев, учиты-вая, что эти определения очень похожи (отличия будем указывать в скобках). Две различные вершины, которые соединены ребром (дугой), т.е. являющиеся концами одного и того же ребра (дуги), называются смежными. В противном случае две вершины не смежны. Множество X вершин графа G, любые две из которых не смежны, называется внутренне устойчивым, а мак- симально возможное число элементов внутренне устойчивого множества − числом внутренней устойчивости графа G. Число вершин, смежных любой вершине графа, называется степенью данной вершины. Множество X вершин графа G называется внешне устойчивым, если любая вершина из V – X, т.е. вершина, не принадлежащая X, смежна хотя бы с одной вершиной из X (является кон-цом некоторой дуги, начало которой принадлежит множеству вершин X). Минимально возмож-ное число элементов внешне устойчивого множества называется числом внешней устойчивос-ти графаG (обозначается β(G)). Множество X вершин графа G, одновременно внутренне и внешне устойчивое, называет-ся ядром графа G. Заметим, что определения внутренне устойчивого множества вершин в обоих случаях сов-падают. Совпадают и определение ядра. Отличаются только определения внешне устойчивого
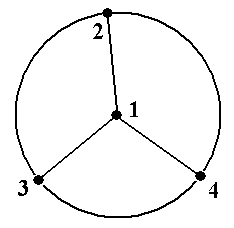
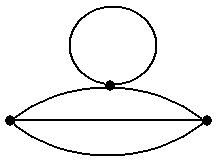
Рис.5. множества: в ориентированном случае требуется, чтобы дуга, соединяющая множества X и V – X, имела направление от X к V – X. Содержательный смысл такого понятия будет прояснён в разделе 5.2. Обратим внимание на следующее. По приведённым выше определениям, любое одноэле-ментное множество вершин является внутренне устойчивым в силу «ложности посылки»: дейс-твительно, в этом множестве упоминаемые в определении «любые две вершины» просто отсут-ствуют из-за того, что рассматриваемое множество одноэлементно. Множество V всех вершин графа является в силу «ложности посылки» внешне устойчивым: упоминаемая в определении «любая не принадлежащая V вершина» не существует именно потому, что V – это множество всех вершин графа. Из определений внутренней и внешней устойчивости непосредственно сле-дует, что: - любая изолированная вершина графа может быть добавлена к любому не содержащему её внутренне устойчивому множеству и это расширенное множество также будет внутренне устойчивым; - любое внешне устойчивое множество обязано содержать любую изолированную верши-ну. Сформулируем утверждения, относящихся к введённым понятиям. Утверждение 1. Любое подмножество внутренне устойчивого множества внутренне ус-тойчиво ■ Утверждение 2. Любое множество, содержащее внешне устойчивое множество, внешне устойчиво ■ Утверждение 3.Пусть в некотором графе G X – внешне устойчивое множество, Y –внутреннеустойчивое множество, и X Тогда Z – ядро графа G ■ Простым следствием из утверждения 3 является следующее Утверждение 4.Пусть Z – ядро в некотором графе G. Тогда существуют минимальное по включению внешне устойчивое множество X и максимальное по включению внутреннеустой-чивое множество Y, для которых выполнены включения (3) ■ Заметим, что все четыре утверждения верны как в неориентированном, так и в ориентиро-ванном случаях. Однако следующее утверждение верно только для неориентированных графов. Утверждение 5. Любое максимальное по включению (т.е. не содержащееся ни в каком другом) внутренне устойчивое множество является и внешне устойчивым, т.е. является ядром ■ Поскольку в любом неориентированном графе (как и в любом ориентированном) множес-тво, состоящее из одной вершины, является внутренне устойчивым, то существует и макси-мальное по включению внутренне устойчивое множество. А оно, в силу утверждения 5, являет-ся ядром. Утверждение 5 даёт гарантию существования ядра для неориентированных графов. А простой пример отсутствия ядра в орграфе даётся ниже. Пример 7.Проиллюстрируем понятия внутренне и внешне устойчивых множеств вершин в неориентированном графе. Для этого рассмотрим граф, показанный на рис.6 (см. также рис. 1a). В графе на рис.6 двухэлементные множества вершин {1, 3}, {3, 5} и одноэлементные мно-жества вершин {2}, {4} являются максимальными по включению внутренне устойчивыми мно-жествами. Ясно, что внутренне устойчивые множества {1}, {3} и {5} не являются максималь-ными по включению (они содержатся в {1, 3} или {3, 5}), а любое множество, состоящее из трёх или более вершин, в данном графе внутренне устойчивым не является (проверьте!). Поэто-му число внутренней устойчивости α(G) данного графа G равно 2. Никакие двухэлементные множества, кроме {1, 3} и {3, 5}, внутренне устойчивыми не являются (проверьте!). А все одно-элементные множества вершин внешне устойчивы в любом графе и, значит, в данном. Минимальными по включению внешне устойчивыми множествами вершин являются те же самые множества вершин {2}, {4}, {1, 3}, {3, 5}, так как другие одноэлементные множества внешне устойчивыми не являются, а все двухэлементные множества, не содержащие подмно-жеств {2} или {4}, совпадают с одним из множеств {1, 3} или {3, 5}. Наконец, все трёх-, четы-рёх- и пятиэлементные множества вершин содержат одно из этих же четырёх множеств: {2}, {4}, {1, 3}, {3, 5}.
Рис.6 Таким образом, каждое из указанных 4-ёх множеств является одновременно внутренне- и внешне устойчивым и, значит, по определению является ядром. Других ядер в данном графе нет ■ Задание 2а.Вграфах, показанных на рис.5, найти все максимальные по включению внут-ренне устойчивые множества вершин, все минимальные по включению внешне устойчивые множества вершин и все ядра. Задание 2b.Вграфах, показанные на рис.7, найти два ядра с разным числом вершин или установить отсутствие таких ядер. Пример 8. На рис.8 показан орграф из примера 6 (сеть питания) с пронумерованными вер-шинами 1 – 5. В этом орграфе внутренне устойчивыми множествами являются все одноэлемен- тные множества {1}, {2}, {3}, {4}, {5} и двухэлементные множества {1, 3}, {1, 4}, {2, 4}, {4, 5}. Других внутренне устойчивых множеств в данном орграфе нет. Одноэлементных внешне устойчивых множеств в данном случае нет (так как нет ни одной вершины, откуда дуги ведут во все остальные). Единственным двухэлементным внешне устой-чивым множеством является {1, 4} (так как дуги á1, 5ñ, á1, 2ñ и á4, 3ñ ведут из {1, 4} в 5, 2 и 3, т.е. во все остальные вершины, в соответствии с определением). Трёхэлементными внешне ус-тойчивыми множествами являются только множества {1, 2, 4}, {1, 3, 4}, {1, 4, 5} (содержащие {1, 4}). Далее, внешне устойчивыми четырёхэлементными множествами являются {1, 2, 3, 4}, {1, 3, 4, 5} и {1, 2, 4, 5} и, наконец, {1, 2, 3, 4, 5}. В данном графе есть единственное ядро: двухэлементное множества {1, 4}■ Само существование ядра для орграфов, в отличие от неориентированных графов, как ука-зывалось выше, не гарантировано, что демонстрирует следующий Пример 9.Рассмотримпростойорграф без петель, показанный на рис.9. Проверим, что у него нет ядра. Предположим, что ядро состоит из одной вершины 1. Но тогда нет дуги, ведущей из 1 в 3, т.е. оно не является внешне устойчивым. Аналогично, ядро не может состоять из вер-шины 2 или вершины 3. Предположим, что ядро состоит из двух вершин, скажем, вершин 1 и 2. Тогда есть дуга из 2 в 3, т.е. оно является внешне устойчивым. Но оно не является внутренне устойчивым, так как в него входят вершины 1 и 2, соединённые дугой. Аналогично для мно-жеств {1, 3} и {2, 3}. Наконец, множество всех вершин {1, 2, 3} является внешне устойчивым, но не является внутренне устойчивым. Таким образом, в данном орграфе ядер нет ■ Задание 3.Ворграфах, показанных на рис.10, найти 1) одно максимальное и одно минимальное по числу вершин ядро; 2) если все ядра содержат одно и то же число вершин, найти два разных ядра; 3) если имеется всего одно ядро, найти его; 4) если ядер не существует, объяснить этот факт ■
Пути в графах Как и в разделе 2, будем давать определения сразу для неориентированного и ориентиро-ванного случая, указывая отличия в скобках. Наиболее общим понятием является понятие пути (орпути). Путём (орпутём) в графе (орграфе) называется чередующаяся последовательность μ вершин и рёбер (дуг), начинающаяся и кончающаяся в вершинах: μ = áv0, b1, v1, b2, ..., vk-1, bk, vkñ, (4) такая, что вершины vi и vi+1 соединены ребром (дугой) bk. Вершина v0 называется началом пути (орпути) μ, вершина vk – концом пути (орпути) μ, а число k, равное числу рёбер (дуг), входящих в путь (орпуть) – его длиной. Говорят также, что путь μ соединяет вершины v0 и vk (орпуть μ ведёт изv0 в vk). Обратным путём для пути μ на-
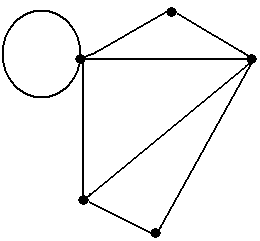
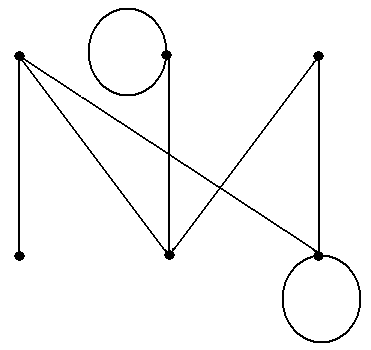
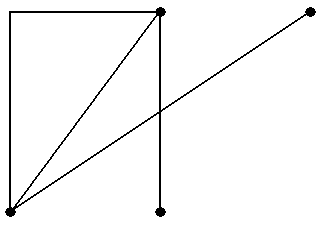
Рис.7
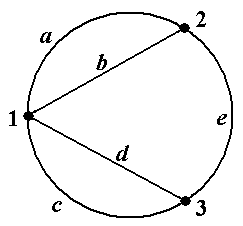
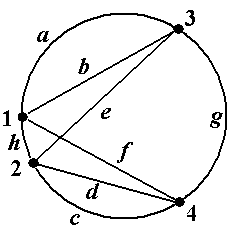
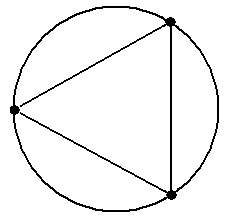
Рис. 10 зывается путь μ-1 = ávk, bk, vk-1, bk-1, ..., v1, b1, v0ñ. Другими словами, путь μ-1состоит из тех же самых вершин и рёбер, но проходимых в обратном порядке. Обратим внимание, что обратный путь определён только в неориентированном случае. Цепью (орцепью) называется путь (орпуть), в котором все рёбра (дуги) различны. Прос-той цепью (орцепью) называется цепь (орцепь), в которой все вершины различны. Путь (орпуть), в котором начало и конец совпадают, называется циклическим путём (орпутём). Циклический путь, являющийся цепью (орцепью), называется циклом (орциклом). Цикл (ор-цикл), в котором все вершины, кроме начала и конца, различны и не совпадают с началом, называется простым циклом (орциклом). Говорят, что не циклический путь ν содержится в не циклическом пути μ, если последова-тельность ν или последовательность ν-1 является подпоследовательностью последовательности μ. В ориентированном случае остаётся только часть этого определения: не циклический орпуть ν содержится в не циклическом пути орпути μ, если последовательность ν является подпоследо-вательностью последовательности μ. Для циклических путей последнее определение требуется модифицировать, учитывая то, что такой путь можно «обходить», начиная с любой вершины, отчего он, конечно же, не изме-нится. Поэтому можно дать такие четыре определения: 1) не циклический путь ν содержится в циклическом пути μ, если последовательность μ можноциклически перенумеровать так, что последовательность ν или последовательность ν-1 станет подпоследовательностью этой перенумерованной последовательности μ; 2) не циклический орпуть ν содержится в циклическом орпути μ, если последовательность μ можноциклически перенумеровать так, что последовательность ν станет подпоследователь-ностью этой перенумерованной последовательности μ; 3) циклический путь ν содержится в пути μ, если последовательность ν или последова-тельность ν-1 можноциклически перенумеровать так, что эта перенумерованная последователь-ность ν станет подпоследовательностью последовательности μ; 4) циклический орпуть ν содержится в орпути μ, если последовательность ν можноцикли-чески перенумеровать так, что эта перенумерованная последовательность ν станет подпоследо-вательностью последовательности μ. Эти на первый взгляд сложные понятия разъясняются далее (см. пример 13). Все вышеприведённые в данном разделе понятия относятся к произвольным графам и ор-графам (см. раздел 1.1). В случае простых графов и орграфов понятие пути (орпути) упрощает-ся: под путём (орпутём) понимается последовательность вершин μ =áv0, v1, ..., vk-1, vkñ, (5) такая, что множество вершин {vi , vi+1} определяет ребро графа (петлю, если vi и vi+1 совпадают) (пара вершин ávi , vi+1ñ определяет дугу орграфа (петлю, если vi и vi+1 совпадают)). Напомним, что в простых графах (орграфах) пара вершин однозначно определяет ребро (дугу), в то время как в графах общего вида таких рёбер (дуг) может быть несколько (см. рис.3, а также рис.5.1 и 10.1). Соответственно упрощаются все остальные приведённые выше определения – достаточно указывать только последовательности вершин. Приведём примеры, иллюстрирующие и разъясняющие введённые понятия. Пример 10. В графе, показанном на рис.11 (копия рис.5-6), обратным к пути μ = á1, f, 4, d, 2, c, 4, g, 3ñ является путь μ-1= á3, g, 4, c, 2, d, 4, f, 1ñ. Обратным к циклическому пути μ =á1, f, 4, d, 2, e, 3, b, 1ñ является циклический путь μ-1 = á1, b, 3, e, 2, d, 4, f, 1ñ (проверьте!) ■ Пример 11.В графе, показанном на рис.12 (копия рис.5-7), обратным к простому пути μ = á2, 1, 4, 3ñ является путь простой путь μ-1 = á3, 4, 1, 2ñ. Обратным к циклическому пути μ-1 = á2, 4, 1, 3, 4, 2ñ является циклический путь μ-1 = á2, 4, 3, 1, 4, 2ñ ■ Пример 12. В графе, показанном на рис.13 (копия рис.5-3) последовательность μ = á1, d, 3, e, 2, b, 1, a, 2, b, 1, c, 3ñ является путём с началом в вершине 1 и концом в вершине 3. Его длина, т.е. число входящих в него рёбер, равно 6. Этот путь не является цепью, так как не все его рёбра различны (ребро b встречается два раза). В этом же графе последовательность ν = á1, d, 3, e, 2, b, 1, c, 3ñ является цепью с началом в вершине 1 и концом в вершине 3. Эта цепь не является простой, так как в ней не все вершины различны (вершины 1 и 3 встречаются по два раза). По-следовательность λ = á1, d, 3ñ является простой цепью. Последовательность λ* = á1, c, 3ñ также
является простой цепью, отличной от простой цепи λ = á1, d, 3ñ (см. рис.13). Заметим, что все четыре рассмотренных в примере пути μ, ν, λ, λ* соединяют одну и ту же пару вершин 1 и 3 ■ Пример 13. Граф, показанный на рис.14 (копия рис.7-c) является простым графом, поэто-му для задания путей можно пользоваться упрощёнными последовательностями, состоящими только из вершин. Последовательность μ = áD, C, G, E, C, B, G, E, Fñ является путём с началом в вершине D и концом в вершине F; его длина равна 8. Путь μ не является цепью, так как ребро {G, E} входит в него дважды. Последовательность ν = áD, C, G, E, C, B, Fñ является цепью, так как все её рёбра не повторяются (проверьте!), но она не является простой цепью, так как вершина C встречается в ней два раза. Последовательность λ = áD, C, B, Fñ является простой цепью, поскольку все её вершины различны. Заметим, что все три рассмотренные пути – μ, ν, λ – соединяют одну и ту же пару вершин D и F ■
Замечания в конце примеров 12 и 13 приводят к достаточно простому умозаключению, сформулированному в следующем утверждении. Утверждение 6. Для всякого пути (орцепи), соединяющего две разные вершины, есть содержащаяся в нём цепь (орцепь), соединяющая те же две вершины. Для всякой цепи (орцепи), соединяющей две вершины, есть содержащаяся в ней простая цепь (орцепь), соединяющая те же две вершины ■ Заметим, что существующая в силу утверждения 6 цепь может совпадать с содержащим её путём (если сам путь уже является цепью); существующая в силу утверждения 6 простая цепь может совпадать с содержащей её цепью (если сама эта цепь уже является простой цепью). Пример 14. В графе, показанном на рис.15 (копия рис.5-15) последовательность μ = á1, a, 2, b, 1, a, 2ñ является путём. Этот путь не является цепью, поскольку он проходит два раза по ребру a. Двумя содержащимися в этом пути цепями являются только цепи ν = á1, a, 2ñ и ν* = á1, b, 2ñ. Обе эти цепи уже являются простыми, и поэтому любая содержащаяся в одной из них простая цепь совпадает с содержащей цепью ■ Заметим также, что во всех рассмотренных в примерах 12 − 14 путях начальная и конеч-ная вершины всегда различны, т.е. ни один из них не является циклическим путём. Задание 4.Вграфах, показанных на рис.5, найти 1) путь, не являющийся цепью; 2) содержащуюся в найденном в 1) пути цепь, не являющуюся простой, соединяющую те же самые вершины; 3)содержащуюся в найденной в 2) цепи простую цепь, соединяющую те же самые верши-ны.
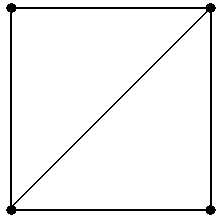
Если некоторые искомые объекты не существуют (как в примере 14), то объяснить это ■ Задание 5.Вграфах, показанных на рис.7, найти 1) путь, не являющийся цепью; 2) не содержащуюся в найденном в 1) пути цепь, не являющуюся простой; 3) не содержащуюся в найденной в 2) цепи простую цепь. Если некоторые искомые объекты не существуют, то объяснить это ■ Пример 15.Рассмотрим простой граф, показанный на рис.16 (копия рис.5-9). Не цикли- ческий путь μ = á6, 2, 5ñ содержится в циклическом пути ν = á2, 5, 3, 6, 2ñ, хотя последователь-ность μ не является подпоследовательностью последовательности ν. Действительно, если тот же самый циклический путь ν начать с вершины 6, т.е. записать в виде ν = á6, 2, 5, 3 ,6ñ, то после такой перенумерации последовательность μ становится подпоследовательностью последова-тельности ν. Рассмотрим теперь не циклический путь μ = á4, 1, 5ñ и циклический путь ν = á1, 4, 2, 5, 1ñ. Последовательность á4, 1, 5ñ не является подпоследовательностью ни самой последова-тельности ν,ни любой её циклической перестановки: á4, 2, 5, 1, 4ñ, á2, 5, 1, 4, 2ñ, á5, 1, 4, 2, 5ñ. Однако обратная последовательность μ-1= á5, 1, 4ñ содержится в циклически переставленной ν = á4, 2, 5, 1, 4ñ, и, значит, в силу введённых определений, путь μ = á4, 1, 5ñ содержится в цикли-ческом пути ν ■
Пример 16. В графе, показанном на рис.13, последовательность μ = á1, d, 3, е, 2, е, 3, с, 1, b, 2, a, 1ñ является циклическим путём, но не является циклом, поскольку ребро е входит в него дважды. Содержащийся в пути μ путь ν = á1, d, 3, с, 1, b, 2, a, 1ñ является циклом, но не является простым циклом, так начальная и конечная вершина 1 входит в него 3 раза, вместо двух, требу-емых определением. Наконец, содержащийся в пути ν путь λ = á1, d, 3, с, 1ñ является простым циклом ■ Пример 17.В графе, показанном на рис.14, последовательность μ = áE, C, G, B, A, F, B, G, Eñ является циклическим путём, но не является циклом, поскольку ребро {G, B} входит в него дважды. Содержащийся в пути μ путь ν = áE, C, B, A, F, B, G, Eñ является циклом, но не является простым циклом, так вершина B входит в него 2 раза. Наконец, содержащийся в пути ν путь λ = áE, C, B, G, E ñ является простым циклом ■ Имеет место утверждение, аналогичное утверждению 7 для не циклических путей. Утверждение 7. Для всякого циклического пути (орпути) есть содержащийся в нём цикл (орцикл). Для всякого цикла (орцикла) есть содержащийся в нём простой цикл (орцикл) ■ Задание 6.Вграфах, показанных на рис.5, найти 1) циклический путь, не являющийся циклом; 2) содержащийся в найденном в 1) пути цикл, не являющийся простым; 3) содержащийся в найденном в 2) цикле простой цикл. Если некоторые искомые объекты не существуют, то объяснить это ■ Задание 7.Вграфах, показанных на рис.7, найти 1) циклический путь, не являющийся циклом; 2) не содержащийся в найденном в 1) пути цикл, не являющийся простым; 3) не содержащийся в найденном в 2) цикле простой цикл. Если некоторые искомые объекты не существуют, то объяснить это ■ Пример 18. В орграфе, показанном на рис.17 (копия рис.10-3) последовательность μ = á1, b, 2, a, 1, d, 3, c, 1ñ является циклическим орпутём, который является орциклом. Этот орцикл содержит два простых цикла: ν1 = á1, b, 2, a, 1ñ и ν2 =á 1, d, 3, c, 1ñ. Кроме них, в данном орграфе есть простой орцикл á1, d, 3, e, 2, a, 1ñ ■ Пример 19.В орграфе, показанном на рис.18 (копия рис.10-4) имеется два орцикла: á1, 2, 3, 4, 5, 6, 1ñ и á7, 7ñ. Они оба являются простыми орциклами ■
Задание 8.Ворграфах, показанных на рис.10, найти 1) циклический орпуть, не являющийся орциклом; 2) содержащийся в найденном в 1) орпути орцикл, не являющийся простым; 3) содержащийся в найденном в 2) орцикле простой орцикл. Если некоторые искомые объекты не существуют, то объяснить это ■ Задание 9.Ворграфах, показанных на рис.10, найти 1) циклический орпуть, не являющийся орциклом; 2) не содержащийся в найденном в 1) пути орцикл, не являющийся простым; 3) не содержащийся в найденном в 2) орцикле простой орцикл. Если некоторые искомые объекты не существуют, то объяснить это ■

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
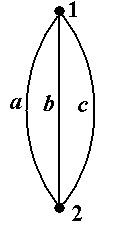



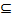 Z
Z 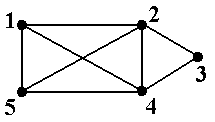
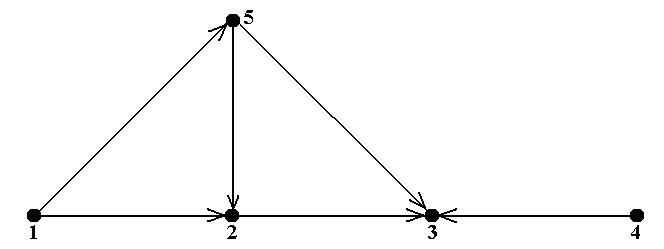 Рис.8
Рис.8
 Рис.9
Рис.9
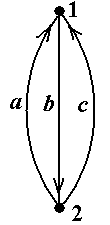

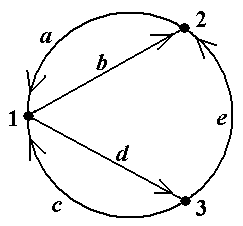
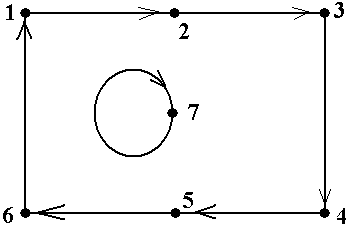
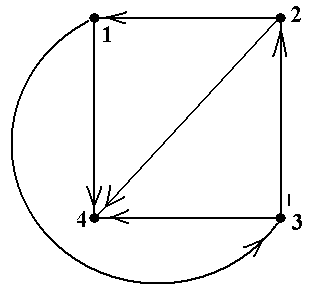

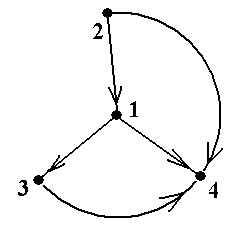
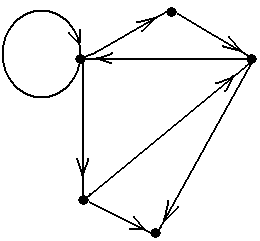
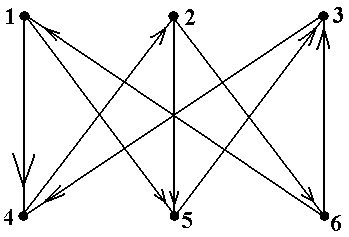
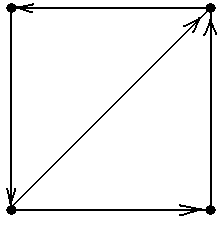

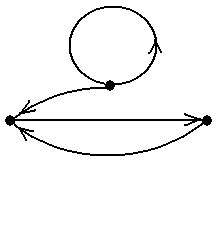
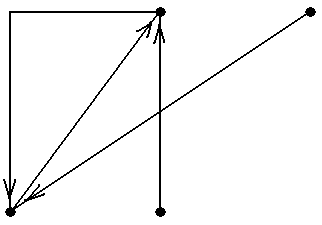
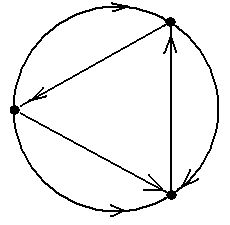
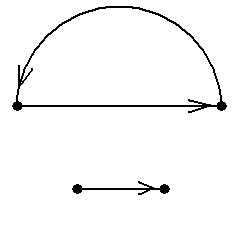
 Рис.14
Рис.14
 Рис.15
Рис.15