
|
|
Понятие Эйлерова и Гамильтонова графов. Понятие Эйлерова пути, цикла, маршрута. Понятие гамильтонова цикла, пути, маршрута.Кольцевая сумма графов Кольцевой суммой графов
На рисунке изображены графы Операция отождествления вершин графа Пусть Пример
Граф
13.Операция произведения графов Операция стягивания графов Стягивание графа - преобразование графа путем последовательного применения операции стягивания ребра.
Граф G стягивается к графу Петерсена H. 15. Операция соединения графов Операция дополнения графа. Операция "объединение графов": результатом объединения графов G1=(V1, E1) и G2=(V2, E2), обозначается Понятие связного графа. Понятие компоненты связности. Сильная связность. Одностороння связность. Слабая связность. Граф называется связным, если имеется путь между любыми двумя его вершинами. Связный граф — Связный граф граф, содержащий ровно одну компоненту связности. Это означает, что между любой парой вершин этого графа существует как минимум один путь Граф называется связным, если 2 любые его вершины можно соединить цепью. Граф называется связным, если любые две его несовпадающие вершины соединены маршрутом. Компонента связности графа — некоторое множество вершин графа такое, что для любых двух вершин из этого множества существует путь из одной в другую, и не существует пути из вершины этого множества в вершину не из этого множества. Сильная связность означает взаимную достижимость любой пары вершин в «обе стороны», т.е. с учетом ориентации дуг и в прямом, и в обратном направлении. Односторонняя связность соответствует взаимной достижимости, по крайней мере, в одну сторону для любой пары вершин. При этом нет сильной связности. Слабая связность определяется как связность только на уровне неориентированного графа, получающегося из орграфа путем исключения петель и стрелок (дуги превращаются в ребра)
на рисунке изображены связные графы Матрица смежности вершин графа. (Орграфа) Матрица смежности — один из способов представления графа в виде матрицы. строки и столбцы – вершины. Матрица симметрична относительно главной диагонали.
Матрица инцидентности графа.(орграфа) Вторая разновидность матричного представления графов – матрица инцидентности. Строки – ребра, столбцы – вершины. В каждой строке ровно 2 единицы.
Понятие плоского графа. Плоский граф — это граф, нарисованный таким образом, что его ребра не пересекаются. Говорят, что граф допускает плоскую укладку, если его можно нарисовать как плоский. Также плоские графы называют планарными.
Понятие подграфа. Подграфом графа называется граф, являющийся подмоделью исходного графа. Иначе говоря, подграф содержит некоторые вершины исходного графа и некоторые рёбра (только те, оба конца которых входят в подграф).
22. Понятие планарного графа. Планарный граф — граф, который может быть изображен на плоскости без пересечения ребер. 23. Понятие грани планарного графа. Грань планарного графа — многоугольник, образованный ребрами графа, диагонали которого не являются ребрами графа (то есть циклы, не распадающиеся на более короткие циклы). Особый случай — внешняя граньграфа: это часть плоскости, являющаяся дополнением к объединению всех вершин, ребер и обычных граней графа. 24. Понятие границы планарного графа. Граница грани – множество вершин и ребер, принадлежащих этой грани. Граница грани является циклом 25. Теорема Эйлера для связных планарных графов.
(Эйлера). Для связного плоского графа верно равенство V − E + F = 2. Доказательство. Пусть на плоскости изображен некоторый граф G. Удалим некоторые ребра из данного графа так, чтобы получилось какое-нибудь остовное дерево этого графа. Поскольку число вершин любого дерева на одну больше числа числа ребер, то для этого дерева E = V − 1, F = 1, и доказываемая формула верна. Теперь начнем восстанавливать исходный граф G из его остовного дерева, для чего будем последовательно добавлять по одному удаленные ребра. При добавлении ребра число вершин никак не меняется, а вот число ребер и число граней увеличивается на 1. Поэтому равенство при добавлении ребра остается верным, а значит окажется верным и после добавления любого числа ребер, в частности для исходного графа G. Буквы V , E и F являются начальными буквами английских слов «vertex», «edge» и «face», которые как раз и переводятся как «вершина», «ребро» и «грань» 26. Планарные/непланарные графы. (Теоремы). Критерии планарности.
Граф планарен тогда и только тогда, когда в нем нет подграфов, стягиваемых к графам к5 или к3,3 Мера непланарности: Для непланарных графов вводятся характеристики, представляющие ту или иную меру непланарности Если граф непланарен, то для его геометрической реализации удаляются отдельные ребра(их переносят на другую плоскость) Наименьшее число ребер, удаление которых приводит к планарному графу, называется числом планарности или искаженностью
Понятие Эйлерова и Гамильтонова графов. Понятие Эйлерова пути, цикла, маршрута. Понятие гамильтонова цикла, пути, маршрута. Эйлеров граф — граф, содержащий эйлеров цикл. Эйлеров цикл — это эйлеров путь, являющийся циклом. Эйлеров путь (эйлерова цепь) в графе — это путь, проходящий по всем рёбрам графа и притом только по одному разу. На рисунке Эйлеров граф
Гамильтонов граф —это граф, содержащий гамильтонову цепь или гамильтонов цикл. Гамильтонов путь (или гамильтонова цепь) — путь (цепь), содержащий каждую вершину графа ровно один раз. Гамильтонов путь, начальная и конечная вершины которого совпадают, называется гамильтоновым циклом. Гамильтонов цикл является простым остовным циклом

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 и
и  называется граф
называется граф  , порожденный на множестве ребер
, порожденный на множестве ребер  , т. е. на множестве ребер, присутствующих либо в
, т. е. на множестве ребер, присутствующих либо в 
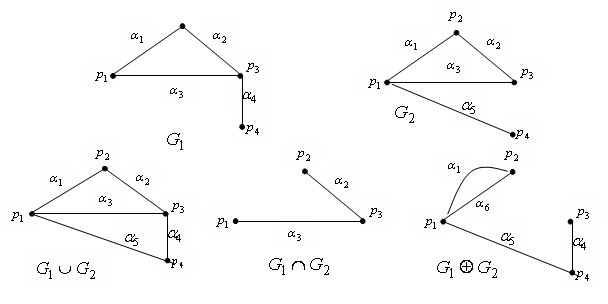
 ,
,  .
. и
и  –две вершины графа
–две вершины графа  . Удалим эти вершины из графа
. Удалим эти вершины из графа  и добавим новую вершину
и добавим новую вершину  , соединив ее ребром с каждой вершиной, входящей в объединение окружений вершин
, соединив ее ребром с каждой вершиной, входящей в объединение окружений вершин  , если
, если  .
. Граф
Граф  получили из графа
получили из графа  получили из графа
получили из графа 

 , является граф G=(V, E), где
, является граф G=(V, E), где 









 на рисунке гамильтонов граф
на рисунке гамильтонов граф