
|
|
Подготовка образца для проведения наблюденийБелорусский государственный университет
Физический факультет Кафедра общей физики
Методические указания К лабораторной работе «Изучение явления броуновского движения»
Минск 2006 Авторы – составители: Жолнеревич И.И. – зав.кафедрой общей физики, доцент Филипп А.Р. – старший преподаватель Кругликов В.В. – лаборант ИЗУЧЕНИЕ БРОУНОВСКОГО ДВИЖЕНИЯ Задание: Изучить явление броуновского движения, экспериментально проверить выполнение формулы Эйнштейна для среднеквадратичного смещения броуновской частицы. Оборудование и принадлежности: установка для проведения исследования, эмульсия для наблюдения броуновского движения.
Описание установки
Установка состоит из трех блоков: микроскопа 2, цифровой телекамеры 3, установленной в тринокуляр микроскопа и персонального компьютера 1.
Изображение, попадающее на ПЗС-матрицу цифровой телекамеры, преобразуется ею в цифровой сигнал, который подается на USB-вход компьютера. С помощью дополнительного программного обеспечения (в лабораторной работе используется специализированная программа АМСар) можно наблюдать увеличенное изображение частиц на экране монитора в режиме реального времени, а также захватывать и математически обрабатывать полученное изображение. Предметом исследования служит эмульсия, приготовленная из молока с низким содержанием жира, для контрастности подкрашенная йодом. Капля раствора, помещенная между предметным и покровным стеклом (толщина последнего составляет 0,17мм) изучается в проходящем свете. В качестве броуновских частиц рассматриваются капельки жира диаметром 0,2 ¸ 1 мкм.
Теория вопроса
Броуновское движение – непрерывное, беспорядочное перемещение малых частиц вещества, взвешенных в жидкости или газе, - представляет собой одно из наиболее ярких и доступных наблюдению подтверждений основных положений молекулярно-кинетической теории вещества. Взвешенная в жидкости, броуновская частица совершает хаотическое движение под действием ударов молекул. Вследствие их хаотического движения, импульс, передаваемый частице за макроскопически малый промежуток времени, является случайной величиной. Следовательно, случайной величиной будет и сила
Сила Следуя Эйнштейну
Для шарообразной частицы подвижность была теоретически вычислена Стоксом:
где η – вязкость жидкости, a – радиус частицы. Уравнение движения (2) в проекции на некоторое направление х будет
Очевидно, что средние значения проекций ускорения
Используя очевидные равенства
Если предположить, что к системе броуновских частиц применима эргодическая гипотеза, то можно провести усреднение выражения (4) по ансамблю частиц. Поскольку операции усреднения и дифференцирования коммуникативны (перестановочны), то получим
Вследствие того, что броуновская частица находится в тепловом равновесии со средой, то по теореме о равнораспределении энергии по степеням свободы,
общее решение которого имеет вид
где
и
Если
Т.е. при малых промежутках времени t броуновская частица движется равномерно со средней скоростью теплового движения. При
Так как r2= x2+ y2+ z2, то <r2>=< x2>+< y2>+< z2>, вследствие изотропности броуновского движения < x2>=< y2>=<z2>. Поэтому
Таким образом, средний квадрат смещения броуновских частиц пропорционален времени t наблюдения (формула Эйнштейна).
Теория метода
Исходя из (9) смещение частицы в плоскости xOy равно
где Проверим выполнение формулы Эйнштейна (11) на опыте. Получим значения Для каждого нового значения t нет необходимости делать свою выборку смщений Δs. Получив лишь одну выборку координат положения частицы через равные промежутки времени t (предположим, мы сделали п измерений), в качестве значений t можно взять, например, следующие значения: t1 =t, t2 =2t, t3 =3t, t4 =4t. Тогда соответствующие значения среднеквадратичных смещений частицы Таблица.1 Пример обработки результатов измерений.
Выполнение задания
Подготовка образца для проведения наблюдений Поместите каплю эмульсии на предметное стекло, а сверху накройте её покровным стеклом. Эмульсия равномерно заполнит пространство между стеклами. По краю покровного стекла следует нанести масло, чтобы исключить интенсивное испарение эмульсии и связанные с ним направленные потоки броуновских частиц. Для нанесения масла используйте шприц с тонкой иглой.
Включите выключатель 10. Переведите тягу 5 в положение для наблюдения через окуляры (вдвинуть до упора). Используя ручку 14 вертикального перемещения столика микроскопа, осторожно поднимите столик таким образом, чтобы объектив микроскопа слегка коснулся капли иммерсионного масла. (Внимание! Действуйте очень осторожно, используя ручку плавной подачи, чтобы не повредить покрытие объектива микроскопа. Наблюдайте за этим процессом сбоку, а не через окуляры.) Для улучшения четкости и контрастности изображения воспользуйтесь регулятором освещенности 11, ручкой управления диафрагмы 9 и ручкой вертикального перемещения столика микроскопа 14. 2. Порядок выполнения задания
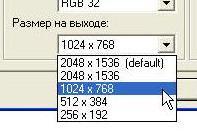
1. Визуальным наблюдением в окуляры микроскопа убедитесь в хаотичности движения броуновских частиц. 2. Получите изображение на экране монитора. Для чего: 2.1. переведите ручку 11 в положение наименьшей яркости, чтобы не пересветить оптическую матрицу телекамеры. 2.2. Вытяните тягу 5 до упора - в положение для наблюдения на экране монитора. 2.3. Запустите программу АМСар, дважды кликнув её значок на рабочем столе компьютера. 2.4. Задайте разрешение изображения. Для этого: выбрав в главном меню программы AMCap раздел “Options”, в выпадающем меню выберите “Video Capture Pin...”, и в открывшемся окне задайте параметр “Размер на выходе” равным 1024х768. Нажмите кнопку ОК.
2.5. Постепенно увеличивая яркость подсветки ручкой 11, добейтесь оптимального изображения на экране. 3. Сохраните на жесткий диск не менее 100 снимков различных положений броуновской частицы с помощью программы HyperSnap. Для чего: 3.1. Запустите программу HyperSnap, кликнув её значок на рабочем столе компьютера. Программа предназначена для “захвата” изображения с экрана монитора. 3.2. На диске D создайте папку, в которой программа HyperSnap будет сохранять полученные изображения. Можно назвать её своей фамилией (Пример: D:\Сидоров\). 3.3. Настройте параметры программы HyperSnap, кликнув на значок “Настройки захвата” 3.3.1. Закладка “Захват”: 3.3.2. Закладка “Быстрое сохранение”: После выставления всех параметров нажмите кнопку ОК в окне настроек. 3.4. Сохраните последовательность снимков рабочего стола с открытым окном программы AMCap на жестком диске компьютера. Для этого: 3.4.1. Наблюдая за изображениями броуновских частиц в окне программы AMCap, выберите частицу для наблюдений. Это должна быть не очень большая в сравнении с остальными частица, которая в то же время не выходит из поля зрения в процессе своего движения. Используя ручку 12 горизонтального перемещения столика микроскопа, поместите изображение частицы в центр окна. 3.4.2. В программе HyperSnap зайдите в меню “Захватить” и выберите пункт “Весь экран”. В результате этого программа HyperSnap свернется на панель задач и начнет сохранять каждые 3 секунды снимки рабочего стола в созданную вами папку (Пример: D:\Сидоров\). 3.4.3. Засеките время, в течение которого вам необходимо делать снимки (Пример: если нужно сделать 100 снимков, то соответственно необходимо ждать 300 секунд). Всё это время курсором мыши сопровождайте выбранную вами частицу, чтобы впоследствии на снимках не спутать ее с другими частицами: 3.4.4. По истечении указанного времени перейдите в программу и ЗАКРОЙТЕ её, выбрав меню “Файл” и пункт “Выход”. Теперь в созданной вами папке содержатся файлы изображений рабочего стола. Номер файла соответствует порядковому номеру снимка (Пример: в папке D:\Сидоров\ будут содержаться файлы броун0001.jpg, броун0002.jpg, … и т.д. – сним攺ов, сделанных через промежутки времени 3 с). 4. Снимите числовые данные координат броуновских частиц и занесите их в таблицу. Для этого: 4.1. Снова откройте программу HyperSnap и откройте один из сохраненных снимков, выбрав меню “Файл” пункт “Открыть” (Пример: открыть файл броун0001.jpg из папки D:\Сидоров\). 4.2. Наведите курсор на частицу: 4.3. Перейдите к следующему снимку, используя кнопки “Следующий файл” на панели инструментов: 5. Обработайте полученные данные и проверьте выполнение формулы Эйнштейна, построив экспериментальный график, на котором ординатами точек будут значения
Приложение 1 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

 Стекло с эмульсией устанавливается на столик микроскопа 8. Увеличенное изображение частиц в эмульсии можно рассматривать либо через окуляры микроскопа 4, либо с помощью цифровой телекамеры 3 выводить на экран монитора.
Стекло с эмульсией устанавливается на столик микроскопа 8. Увеличенное изображение частиц в эмульсии можно рассматривать либо через окуляры микроскопа 4, либо с помощью цифровой телекамеры 3 выводить на экран монитора. , действующая на частицу. Согласно второму закону Ньютона, уравнение движения частицы имеет вид
, действующая на частицу. Согласно второму закону Ньютона, уравнение движения частицы имеет вид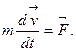
 - случайной силы со средним значением равным нулю <
- случайной силы со средним значением равным нулю <  где b – подвижность частицы.
где b – подвижность частицы.
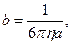
 или
или 
 и силы
и силы  равны нулю. Умножим все члены уравнения (3) на х:
равны нулю. Умножим все члены уравнения (3) на х:
 и
и  выражение (3) приводим к виду
выражение (3) приводим к виду

 . Кроме того, поскольку смещение x частицы и сила
. Кроме того, поскольку смещение x частицы и сила  являются независимыми случайными величинами, то
являются независимыми случайными величинами, то 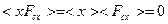 . Обозначив
. Обозначив  в (5) получим неоднородное дифференциальное уравнение
в (5) получим неоднородное дифференциальное уравнение
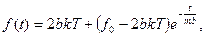
 – значение
– значение  в начальный момент времени, которое можно положить равным нулю. С учетом этого, из (7) следует
в начальный момент времени, которое можно положить равным нулю. С учетом этого, из (7) следует

 , то разложив экспоненту в ряд Маклорена до второго члена включительно, получим
, то разложив экспоненту в ряд Маклорена до второго члена включительно, получим
 из (8) следует, что
из (8) следует, что

 =
=  +
+  =
=  .
. ,‡(11)
,‡(11)
 .
.


 Установив полученный таким образом образец на столик микроскопа 8, выберите объектив со сорокакратным увеличением (40х), и наведите его на образец.
Установив полученный таким образом образец на столик микроскопа 8, выберите объектив со сорокакратным увеличением (40х), и наведите его на образец.
 на панели инструментов программы HyperSnap. В открывшемся окне нас интересуют закладки “Захват” и “Быстрое сохранение”, они должны быть настроены следующим образом:
на панели инструментов программы HyperSnap. В открывшемся окне нас интересуют закладки “Захват” и “Быстрое сохранение”, они должны быть настроены следующим образом: Включить изображение курсора.
Включить изображение курсора.  .
. , старясь разместить его перекрестие точно в центре частицы. Занесите в таблицу (см. Приложение 1) значения координат в правом нижнем углу окна программы:
, старясь разместить его перекрестие точно в центре частицы. Занесите в таблицу (см. Приложение 1) значения координат в правом нижнем углу окна программы:  .
. .
.