
|
|
Водобойный колодец со стенкой (комбинированный колодец)Комбинированный колодец (рис. 9.26) применяется в случаях, когда глубина колодца или высота водобойной стенки существенно большие. Для их устройства требуются значительные капитальные затраты.
Рис. 9.26. Комбинированный колодец При расчете комбинированного колодца должно удовлетворяться условие
Вначале находится высота водобойной стенки ас. Высота определяется исходя из того, что сопряжение потока за стенкой будет иметь форму затопленного прыжка, и согласно (9.51)
где hсс — глубина в сжатом сечении за стенкой; φс — коэффициент скорости, принимается φс = 0,85
где Vос — средняя скорость перед стенкой. Из (9.75) находим глубину колодца:
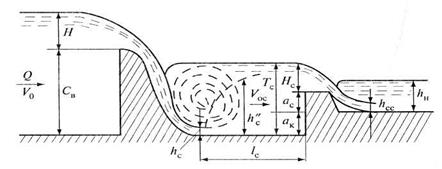
Вычисляя сжатую глубину hс в колодце и сопряженную с ней Длина комбинированного колодца при условии его затопления lк = (0,7 ÷ 0,8) lп , где lп — длина гидравлического прыжка. ♦ Пример 9.7 В канале прямоугольного сечения шириной b = 3 м имеется водослив практического профиля криволинейной формы. Определить характер сопряжения потока расходом 10 м3/с с нижним бьефом и размеры водобойного колодца. Глубина воды в нижнем бьефе hн = 1,8 м (см. рис. 9.24). Высота в нижнем бьефе плотины Сн = 3,0 м, в верхнем бьефе Св = 3,5 м. Полный напор на подходе к водосливной плотине
Напор на водосливной плотине
Принимаем коэффициент расхода m0 = 0,45.
Скорость на подходе к водосливу
Сжатая глубина определяется из уравнения (9.51), принимая φ = 0,95:
Методом подбора получаем hc = 0,395 м,
Критическая глубина
Фиктивная сопряженная глубина
Сопряжение струи с нижним бьефом будет осуществляться в виде отогнанного прыжка. Перепад на колодце по (9.64) при φ = 1:
Глубина колодца, принимая σ =1,1, составит
Длина прыжка по формуле Сафранеца
По формуле М. Чертоусова
Длина колодца lк = 0,75 lп = 0,75 · 10,6 = 8,0 м. Размеры колодца: ак = 0,45 м; lк = 8,0 м. ♦ Пример 9.8 Согласно исходным данным примера 9.7 определить размеры водобойной стенки. Коэффициент расхода стенки m = 0,41 (см. рис. 9.25) Полный напор на водобойной стенке по (9.71)
Скорость перед водобойной стенкой при σ = 1,1
Напор на стенке при α=1
Высота водобойной стенки
Проверяем сопряжение потока за стенкой. Полный напор перед стенкой Тос = ac + Hco = 1,02 + 1,5 = 2,52 м Примем коэффициент скорости φ= 0,95. Сжатую глубину за стенкой находим по зависимости
Подбором находим hсс = 0,58 м. Фиктивная сопряженная глубина
За водобойной стенкой сопряжение потока будет в виде затопленного прыжка. Дополнительной стенки не нужно устанавливать. Расстояние до стенки будет такое же, как и для водобойного колодца, lс = 8,0 м. Размеры стенки: ас = 1,02 м; lс = 8,0 м.
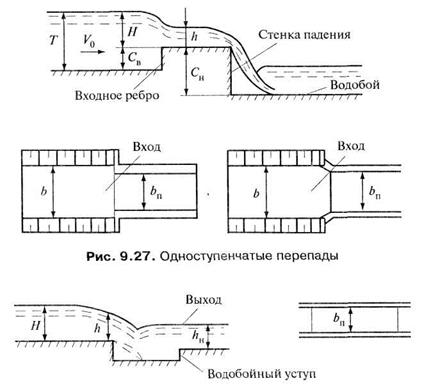
ПЕРЕПАДЫ Перепадом называют сооружение, устанавливаемое в русле, имеющее существенно большой уклон дна и обеспечивающее сопряжение участков потока жидкости по ступеням (уступам). Ступень представляет собой, как правило, вертикальную стенку падения и горизонтальный участок русла. В зависимости от числа ступеней перепады делятся на одноступенчатые (рис. 9.27 и 9.28) и многоступенчатые (см. рис. 9.32). В системах водоотведения при сопряжении двух потоков жидкости в случае резкого изменения рельефа местности устраивают перепадные колодцы. В таких колодцах сопрягается поток в подводящей трубе с потоком в отводящем коллекторе, расположенном на отметке ниже уровня подводящей трубы.
Рис. 9.28. Одноступенчатый перепад с уступом Одноступенчатые перепады В одноступенчатых перепадах форма сечения подводящего русла может отличаться от сечения самого перепада по высоте и ширине. Одноступенчатый перепад состоит из входа, стенки падения, водобоя и выхода (см. рис. 9.27). Геометрические размеры входа и выхода могут быть различны. Водобой представляет собой горизонтальный участок русла, который воспринимает ударное воздействие падающего потока жидкости и гасит ее энергию. Стенка падения может быть вертикальной, с некоторым уклоном к поверхности русла или криволинейной. На рис. 9.29 представлена схема одноступенчатого перепада, у которого высота стенки падения Сн. Глубина потока жидкости на подходе к стенке соответствует глубине h0.
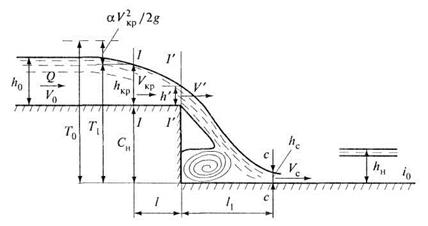
Рис. 9.29. Одноступенчатый перепад В случае если поток жидкости в подводящем призматическом русле находится в спокойном состоянии, i0 < iкр , то в верхнем бьефе до ребра стенки падения возникает кривая спада. На этом участке будет иметь место плавно изменяющееся движение. В сечении непосредственно у ребра 1'-1', как показали экспериментальные исследования, устанавливается глубина h'≈ 0,71hкр. На расстоянии l = (2÷2,5)hкр от ребра стенки падения глубина будет равна критической глубине h1 = hкp . В случае бурного состояния потока и неравномерного его движения глубина в сечении 1-1 должна определяться путем построения кривой свободной поверхности. В результате падения потока со стенки за счет ускорения силы тяжести и силы инерции на участке падения скорость увеличивается. В сечении с-с скорость Vc будет максимальная. В этом сечении будет происходить сжатие потока и глубина равна hc. Сжатая глубина будет меньше критической глубины hкр. Поскольку hс < hкp , то за стенкой падения возникает гидравлический прыжок, в начале которого глубина равна hс. В отводящем русле поток имеет глубину hн. Струя жидкости, обладая запасом кинетической энергии, определяемой скоростью V' у ребра стенки падения, отлетает на расстояние l1 Расстояние отсчитывается от стенки до сжатого сечения с-с. Уравнение для определения глубины в сжатом сечении hс может быть получено путем использования уравнения Бернулли для сечений 1-1 и с-с. Плоскость сравнения принимается на уровне дна нижнего бьефа перепада. Уравнение, которое получим, будет аналогично уравнению (9.51):
Полная удельная энергия для сечения 1-1
где V1 — скорость в сечении 1-1, V1 = Vкр:
Согласно исследованиям ряда авторов, коэффициент скорости при
Модельные исследования перепадов прямоугольного сечения, проведенные Б. Ботуком, позволили определить функциональную зависимость коэффициента скорости от параметров Сн, Но, b, В:
где b — ширина перепада; B — ширина свободной входной части. На рис. 9.30 приведен график функции коэффициента скорости φ перепада, если имеется доступ воздуха под струю жидкости. В зависимости от глубины в нижнем бьефе перепада сопряжение потоков может иметь форму отогнанного прыжка или затопленного прыжка. Если hc" > hH — отогнанный прыжок, при hc"< hH — затопленный прыжок, hc" — фиктивная глубина сопряжения со сжатой глубиной hс.
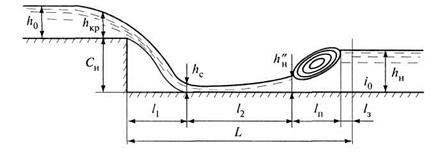
Рис. 9.30. График функции На рис. 9.31 показана схема перепада, где сопряжение бьефов имеет форму отогнанного прыжка.
Рис. 9.31. Перепад с отогнанным прыжком На участке отводящего русла, где заканчивается гидравлический прыжок, скорости потока существенно превышают скорости при нормальной глубине h0. На этом участке длиной L требуется укрепление дна русла, чтобы предотвратить его гидравлический размыв. Участок длиной L называется водобоем. Общая длина водобойного участка L = l1+l2+lп+l3, (9.81) где l1, — дальность отлета струи; l2 — длина отгона прыжка; lп — длина прыжка; lз — длина запаса. Длина запаса учитывает необходимость крепления дна водобоя за пределами гидравлического прыжка: l3 = (1÷2) hн. (9.82) Дальность отлета струи может быть вычислена по формуле, полученной согласно уравнению траектории физического тела, имеющего начальную скорость V' на уступе перепада, где глубина h' = 0,71hкр (см. рис. 9.27): Дальность отлета также может быть вычислена по формуле (9.69). Длина отгона прыжка l2 находится, как длина кривой подпора (свободной поверхности). Начальная глубина свободной поверхности hс, конечная длина h"н — сопряженная глубина с глубиной в русле hн. Длина прыжка lп определяется по формулам, приведенным в гл. 8. В случае сопряжения бьефов в виде затопленного прыжка длина l2 = 0. Расчет одноступенчатого перепада заключается в определении глубины на входном участке и на водобое, высоты стенки падения и длины водобоя. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 . (9.75)
. (9.75) . (9.76)
. (9.76) 0,95; Нсо — полный напор перед стенкой;
0,95; Нсо — полный напор перед стенкой;  — сопряженная глубина с глубиной в отводящем русле прямоугольного сечения hH, вычисляется по формуле
— сопряженная глубина с глубиной в отводящем русле прямоугольного сечения hH, вычисляется по формуле
 ,
, ,
, . (9.77)
. (9.77) .
.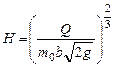
 .
.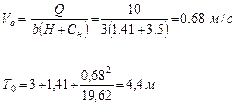
 .
.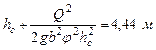 .
.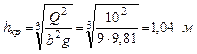
 .
. .
. .
. .
. .
.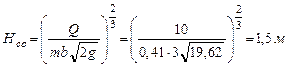 .
.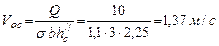
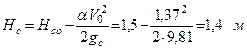
 .
. .
. составит
составит .
.
 .
. , (9.78)
, (9.78) . (9.79)
. (9.79) находится в пределах φ= 0,75
находится в пределах φ= 0,75 
 f
f  , (9.80)
, (9.80)
 f
f 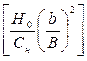
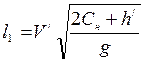 . (9.83)
. (9.83)