
|
|
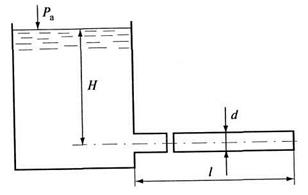
ИСТЕЧЕНИЕ ЖИДКОСТИ ЧЕРЕЗ БОЛЬШИЕ ОТВЕРСТИЯГлава 6. ИСТЕЧЕНИЕ ЖИДКОСТИ ЧЕРЕЗ ОТВЕРСТИЯ И НАСАДКИ ОБЩИЕ СВЕДЕНИЯ И ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ИСТЕЧЕНИЯ Истечение жидкости из какого-либо резервуара может происходить через отверстия различных размеров и форм, насадки и короткие трубы в различных условиях. На рис. 6.1 изображен резервуар, в вертикальной боковой стенке его имеется малое отверстие. Истечение из отверстия может быть при постоянном напоре Н и давлении
Рис. 6.1. Истечение жидкости из малого отверстия Н - заглубление центра отверстия диаметром d под уровень свободной поверхности. Если Н и Струя из отверстия может истекать в атмосферу или под уровень жидкости, когда вытекающая струя будет распространяться в каком-то другом резервуаре или сосуде, в котором находится жидкость. При истечении в атмосферу отверстие будет незатопленным, так же как и струя, вытекающая из него. Когда истечение происходит под уровень жидкости, отверстие является затопленным. Отверстие в резервуаре называется малым, если во всех точках отверстия давление можно считать практически постоянным. Поэтому скорости в разных точках живого сечения струи будут одинаковыми. Обычно к малым отверстиям относятся такие, если диаметр Отверстием в тонкой стенке называется отверстие, когда толщина стенки резервуара Струя жидкости при истечении из отверстия на расстоянии Коэффициент сжатия струи
На сжатие струи влияют границы стенок, которые могут находиться достаточно близко к отверстию. Опытами установлено, что если расстояние от кромок При истечении воды из малых отверстий, как было установлено опытами, в случае совершенного сжатия Несовершенное сжатие происходит при несоблюдении условия, и сжатие струи уменьшается. Большие отверстия - отверстия, в которых давления в пределах живого сечения существенно отличаются от давления на его границах. В связи с этим скорости в разных точках различны. Насадками называют короткие трубы, присоединенные к стенке резервуара, если их длина
ИСТЕЧЕНИЕ ЖИДКОСТИ ЧЕРЕЗ ОТВЕРСТИЯ В ТОНКОЙ СТЕНКЕ ПРИ ПОСТОЯННОМ НАПОРЕ Отверстие незатопленное Для определения скорости и расхода жидкости, вытекающей из отверстия, применяем уравнение Бернулли. Принимаем сечение 1-1 по свободной поверхности жидкости в резервуаре, второе сечение 2-2 проведем через сжатое сечение струи С-С. Плоскость сравнения 0-0 проводим через центр сжатого сечения параллельно свободной поверхности (см. рис. 6.1). Истечение жидкости осуществляется в атмосферу. Напишем уравнение Бернулли для сечений 1-1 и 2-2: где Согласно формуле Вейсбаха
где Принимаем
Следовательно,
Скоростью Величину Тогда
Отсюда скорость в сжатом сечении
Введем следующее обозначение:
uде Окончательно формула скорости истечения будет иметь следующий вид:
Для частного случая, когда
В результате скорость
Для идеальной жидкости потери напора Теоретическая скорость истечения в этом случае
Зависимость (6.9) - формула Торричелли, полученная им в 1643 г. на основании опытов при определении скоростей истечения в случае разных напоров Физический смысл коэффициента Зная скорость истечения, можно найти расход Q. При условии, что
Назовем произведение двух коэффициентов
Тогда выражение для расхода при истечении через отверстие будет
Коэффициент расхода учитывает как степень сжатия, так и потери напора Коэффициент Следует отметить, что при истечении через малые отверстия за сжатым сечением происходит деформация поперечного сечения струи. Форма деформированного сечения отличается от формы сечения отверстия, из которого происходит истечение. Такое явление носит название инверсии струи, которая происходит из-за поверхностного натяжения жидкости. Например, при истечении из круглого отверстия поперечное сечение струи имеет форму эллипса, а для квадратного сечения струя приобретает крестообразную форму. Отверстие затопленное Рассматриваем малое отверстие в тонкой стенке, из которого происходит истечение под уровень жидкости (рис. 6.2). Давления на свободные поверхности жидкости в резервуарах равны атмосферному
Рис. 6.2. Истечение под уровень жидкости Напишем уравнение Бернулли для сечений 1-1 и 3-3 относительно плоскости сравнения, проходящей через центр отверстия параллельно свободным поверхностям в резервуарах:
Пренебрегаем величинами
где Потери напора между выбранными сечениями состоят из потерь при истечении из отверстия, т.е. от сечения 1-1 до 2-2 (С-С) и от сечения 2-2 до сечения 3-3, где происходит внезапное расширение струи до существенно больших размеров:
Потери при истечении из отверстия
Потери при внезапном расширении струи определяем по формуле Борда (4.126):
где Потери напора будут
Скорость в сжатом сечении
или
Формула расхода для сжатого сечения при истечении через затопленное отверстие:
Полученная формула расхода аналогична формуле расхода для незатопленного отверстия. Различие формул заключается в том, что напор истечения Н выражает разность уровней Установлено при проведении многочисленных опытов, что значения
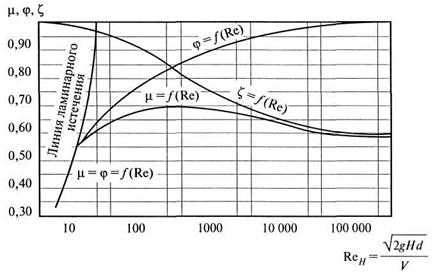
Рис. 6.3. Зависимость коэффициентов истечения из малых отверстий в тонкой стенке от числа Рейнольдса ♦ Пример 6.1 Определить длину трубопровода диаметром Формулы расхода при истечении жидкости из отверстия и трубы:
Площади поперечных сечений отверстия и трубы (
Рис. 6.4. К примерам 6.1 и 6.8 Расходы
Коэффициент расхода малого отверстия Определим число Рейнольдса
По графику (см. рис. 6.3) находим для полученного Re Коэффициент расхода трубы
Возведем в квадрат равенство расходов, полученное ранее:
Откуда
Из полученного выражения находим длину трубопровода:
Длина трубопровода ♦ Пример 6.2 Два резервуара, напоры в которых поддерживаются постоянными и равными соответственно
Рис. 6.5. К примеру 6.2 Напор, при котором происходит истечение воды из одного резервуара в другой,
Расход воды определяется по формуле
Коэффициент расхода короткой трубы
Диаметр трубы находим методом подбора, задаваясь разными значениями d. Вычисления Таблица 6.1 - Результаты вычисления
Диаметру d=50 мм соответствует расход Q=13,3 л/с, что удовлетворяет условию примера.
ИСТЕЧЕНИЕ ЖИДКОСТИ ЧЕРЕЗ БОЛЬШИЕ ОТВЕРСТИЯ Отверстия являются большими, если давление в пределах их живого сечения переменно, а скорость увеличивается по мере удаления от верхней кромки отверстия. Рассмотрим большое отверстие произвольной формы в тонкой стенке (рис. 6.6). Напор по верхней кромке отверстия
где Полагаем, что Расход, проходящий через все горизонтальные полоски, получим, интегрируя
При нахождении расхода по формуле (6.20) необходимо знать функциональную зависимость переменной ширины от высоты большого отверстия.
Рис. 6.6. Истечение из большого отверстия произвольной формы Рассмотрим частный случай большого отверстия прямоугольной формы (рис. 6.7). Ширина отверстия равна
Расход жидкости может быть также вычислен, принимая напор истечения относительно центра тяжести большого отверстия
Рис. 6.7. Истечение из большого прямоугольного отверстия в тонкой стенке
или где Для прямоугольного отверстия площадь отверстия
где Следует отметить, что коэффициент расхода Ориентировочно при определении расхода можно принимать

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
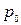 на поверхности жидкости в резервуаре.
на поверхности жидкости в резервуаре.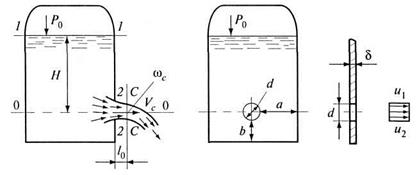
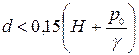 или гидравлический диаметр
или гидравлический диаметр  для других форм отверстий.
для других форм отверстий. не влияет на условия истечения струи. При истечении жидкости потери напора в этом случае практически аналогичны местным потерям в результате внезапного сужения потока. Обычно к отверстиям в тонкой стенке относят случаи, когда
не влияет на условия истечения струи. При истечении жидкости потери напора в этом случае практически аналогичны местным потерям в результате внезапного сужения потока. Обычно к отверстиям в тонкой стенке относят случаи, когда  .
. от входа резко сжимается. На этом расстоянии возникает сжатое сечение С-С (см. рис. 6.1), площадь живого сечения
от входа резко сжимается. На этом расстоянии возникает сжатое сечение С-С (см. рис. 6.1), площадь живого сечения 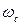 . Как показали опыты, расстояние до сжатого сечения составляет
. Как показали опыты, расстояние до сжатого сечения составляет  . Сжатие струи происходит в результате сил инерции, действующих на частицы жидкости, движущиеся по разным траекториям к самому отверстию. Частицы жидкости, обтекая кромки отверстия, имеют плавную траекторию движения и образуют поверхность струи на участке длиной
. Сжатие струи происходит в результате сил инерции, действующих на частицы жидкости, движущиеся по разным траекториям к самому отверстию. Частицы жидкости, обтекая кромки отверстия, имеют плавную траекторию движения и образуют поверхность струи на участке длиной 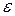
 . (6.1)
. (6.1) и
и  , то боковые стенки и дно резервуара не будут влиять на степень сжатия струи. Такое сжатие получило название совершенного сжатия.
, то боковые стенки и дно резервуара не будут влиять на степень сжатия струи. Такое сжатие получило название совершенного сжатия. .
. (d - диаметр отверстия).
(d - диаметр отверстия). (6.2)
(6.2) - абсолютное давление на свободной поверхности жидкости в резервуаре;
- абсолютное давление на свободной поверхности жидкости в резервуаре; 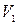 ,
, 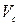 - средние скорости в соответствующих сечениях;
- средние скорости в соответствующих сечениях;  ;
;  - потери напора на участке от сечений 1-1 к 2-2.
- потери напора на участке от сечений 1-1 к 2-2. ,
, - коэффициент местных сопротивлений отверстия.
- коэффициент местных сопротивлений отверстия. .
. (
(  . (6.3)
. (6.3)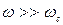 .
. назовем приведенным напором.
назовем приведенным напором. . (6.4)
. (6.4) . (6.5)
. (6.5) , (6.6)
, (6.6) - коэффициент скорости истечения.
- коэффициент скорости истечения. . (6.7)
. (6.7) , т.е. резервуар сообщается с атмосферой,
, т.е. резервуар сообщается с атмосферой, .
. . (6.8)
. (6.8) и
и  , а коэффициент скорости
, а коэффициент скорости 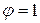 .
. . (6.9)
. (6.9) .
. (
(  ).
). . (6.10)
. (6.10) :
: . (6.11)
. (6.11) . (6.12)
. (6.12) 0,64. Как правило, для предварительных расчетов принимается
0,64. Как правило, для предварительных расчетов принимается  .
.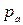 . Поверхности уровней как в правом, так и в левом резервуаре не изменяют своего положения за определенное время.
. Поверхности уровней как в правом, так и в левом резервуаре не изменяют своего положения за определенное время.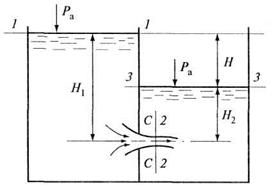
 ;
; ;
;  ;
;  ;
;  (6.13)
(6.13) и
и 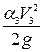 вследствие их малости, так как площади поперечных сечений резервуаров
вследствие их малости, так как площади поперечных сечений резервуаров  и
и  (
(  - площадь малого отверстия). После подстановок получим
- площадь малого отверстия). После подстановок получим , (6.14)
, (6.14) ;
;  - гидравлические потери напора;
- гидравлические потери напора;  - коэффициент сопротивления, учитывающий потери напора от сечения 1-1 до сечения 3-3;
- коэффициент сопротивления, учитывающий потери напора от сечения 1-1 до сечения 3-3;  (6.15)
(6.15) .
. ,
, - скорость в резервуаре при расширении струи,
- скорость в резервуаре при расширении струи, 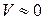 .
.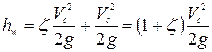 . (6.16)
. (6.16)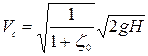 (6.17)
(6.17) . (6.18)
. (6.18)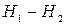 жидкости в резервуарах.
жидкости в резервуарах. , принимаются
, принимаются  ;
;  ;
;  ;
;  .
.
 мм, при котором расход вытекающей воды будет такой же, как из малого отверстия того же диаметра, если напоры воды соответственно равны
мм, при котором расход вытекающей воды будет такой же, как из малого отверстия того же диаметра, если напоры воды соответственно равны  м и
м и  м . Коэффициент гидравлического трения трубы принять равным
м . Коэффициент гидравлического трения трубы принять равным  . Температура воды
. Температура воды  (рис. 6.4).
(рис. 6.4). ;
; .
. ) равны
) равны  .
.
 , тогда
, тогда .
. найдем, используя зависимость
найдем, используя зависимость  (см. рис. 6.3).
(см. рис. 6.3). ,
, м/с2 при
м/с2 при  .
. ,
,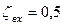 ;
;  (табл. П 1.4 приложения).
(табл. П 1.4 приложения). ,
, ;
; .
. ;
; м.
м. м.
м. м и
м и  м, соединены между собой короткой трубой длиной
м, соединены между собой короткой трубой длиной  м. Расход воды, протекающий из одного резервуара в другой,
м. Расход воды, протекающий из одного резервуара в другой,  л/с. Температура воды
л/с. Температура воды  (рис. 6.5).
(рис. 6.5).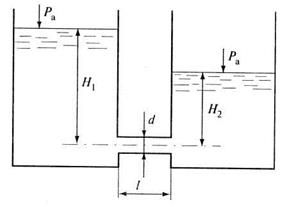
 м.
м. .
.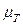 при
при  (табл. П 1.5 приложения)
(табл. П 1.5 приложения) .
. и
и  сводим в табл. 6.1.
сводим в табл. 6.1.
 , по нижней -
, по нижней - 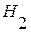 . Выделим в большом отверстии горизонтальную полоску высотой
. Выделим в большом отверстии горизонтальную полоску высотой  , которую будем считать как площадь малого отверстия. Напор для такого отверстия полагаем постоянным и равным Н. Элементарный расход, проходящий через эту горизонтальную полоску,
, которую будем считать как площадь малого отверстия. Напор для такого отверстия полагаем постоянным и равным Н. Элементарный расход, проходящий через эту горизонтальную полоску, , (6.19)
, (6.19) для всех узких горизонтальных полосок, на которые разбивается большое отверстие.
для всех узких горизонтальных полосок, на которые разбивается большое отверстие.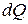 (6.19), а постоянные величины выносим за знак интеграла:
(6.19), а постоянные величины выносим за знак интеграла: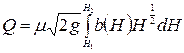 . (6.20)
. (6.20)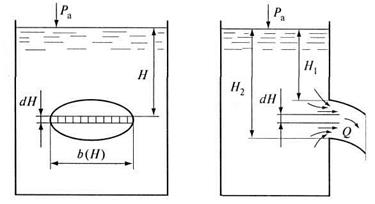
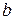 . Расход жидкости для прямоугольного отверстия согласно зависимости (6.20) после интегрирования
. Расход жидкости для прямоугольного отверстия согласно зависимости (6.20) после интегрирования . (6.21)
. (6.21) .
.
 (6.22)
(6.22) , (6.23)
, (6.23) - коэффициент расхода большого отверстия.
- коэффициент расхода большого отверстия. ,
, ,
,  зависит от размеров, формы отверстия, обработки кромок отверстия, влияния стенок на сжатие струи, напора
зависит от размеров, формы отверстия, обработки кромок отверстия, влияния стенок на сжатие струи, напора  при совершенном сжатии и
при совершенном сжатии и  - при несовершенном.
- при несовершенном.