
|
|
РЕЖИМЫ ДВИЖЕНИЯ ВЯЗКОЙ ЖИДКОСТИГлава 4. ГИДРАВЛИЧЕСКИЕ СОПРОТИВЛЕНИЯ ВИДЫ ГИДРАВЛИЧЕСКИХ СОПРОТИВЛЕНИЙ Как уже отмечалось ранее в гл. 3, вязкость жидкости является основной причиной возникновения сопротивления движению и тем самым вызывает потерю части механической энергии, являющейся потерянной энергией. Гидравлическими сопротивлениями можно называть силы вязкостного трения, возникающие в реальной жидкости при ее движении [6]. Сопротивления обусловливаются вязкостными силами трения и способностью самой жидкости сопротивляться изменению и восстановлению формы потока. В случае Движения идеальной жидкости силы трения отсутствуют, поэтому гидравлические сопротивления равны нулю. Имеются два вида сопротивлений: сопротивления по длине и сопротивления местные. Сопротивления, возникающие по длине потока жидкости, - сопротивления по длине. Для преодоления сил гидравлического трения, вектор которых направлен в обратную сторону движения потока жидкости, необходимо затратить механическую энергию. Потери механической энергии обусловлены работой сил трения. Работа сил трения по длине потока характеризуется касательными напряжениями, которые на участке длиной Местными сопротивлениями называются участки потока жидкости, в которых происходит достаточно резкая деформация и средняя скорость изменяется по значению и направлению. Например, деформация связана с изменением сечения потока конечных размеров, переменой направления движения жидкости в трубопроводе. В результате деформации на местном участке имеет место достаточно резко изменяющееся неравномерное движение жидкости с вихреобразованием. Если длина участка сопротивления является весьма малой по сравнению с длиной потока, то потери напора по длине Потери напора, возникающие на отдельных коротких участках потока и связанные с его деформацией, называются местными потерями, обозначаются через Полные гидравлические потери напора при движении жидкости в трубопроводе с участками, где происходит деформация потока, можно выразить как
где Величина механической энергии на преодоление сопротивления движению потока жидкости, связанная с работой сил трения, безвозвратно теряется потоком, переходя в тепло, которое рассеивается со временем. На потерю напора
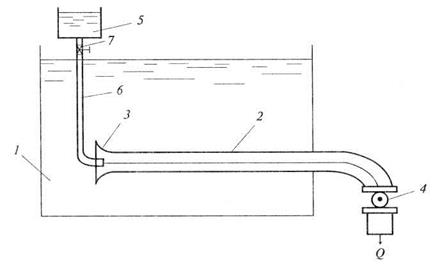
РЕЖИМЫ ДВИЖЕНИЯ ВЯЗКОЙ ЖИДКОСТИ Характер (вид) движения жидкости изучался в 1840 - 1880 гг. в Германии Г. Хагеном и в России Д. Менделеевым. Состояние движения потока может иметь струйчатый или беспорядочный характер. Когда струйчатость нарушается, частички жидкости движутся по весьма сложным траекториям. При струйчатом течении траектория движения частички жидкости ориентирована параллельно стенкам потока конечных размеров. Весьма обширные и обстоятельные исследования по течению жидкости в трубе были проведены в 1883 г. английским ученым О. Рейнольдсом. Лабораторная установка (рис. 4.1), на которой проводились эксперименты, состояла из бака 1, стеклянной горизонтальной трубы 2 диаметром
Рис. 4.1. Схема стенда Рейнольдса: 1 - бак; 2 - стеклянная труба; 3 - мундштук; 4 - кран; 5 - резервуар с раствором; 6 - трубочка; 7 - краник Над баком был установлен небольшой резервуар 5, заполняемый раствором анилиновой краски. К резервуару была присоединена тонкая трубочка 6, конец которой входил в мундштук по оси трубы. Для регулирования пуска раствора краски через трубочку в стеклянную трубу имелся краник 7. Раствор анилиновой краски имел практически одинаковую плотность с водой, находящейся в баке. Опыты заключались в том, что, открывая кран на трубе, устанавливались определенные расход и скорость При достаточно малой скорости в трубе струйка раствора образовывала внутри потока воды устойчивую несмешивающуюся окрашенную тонкую струйку. Данный опыт демонстрировал существование струйчатого характера движения жидкости. Несколько увеличивая среднюю скорость, наблюдалось такое же движение окрашенной струйки. Движение жидкости, которому соответствует устойчивый струйчатый характер, является ламинарным движением. Название движения произошло от латинского слова lamina - слой. Ламинарный режим соответствует относительно малым скоростям и слоистому движению жидкости. Частички жидкости не перемешиваются друг с другом, и линии тока параллельны оси движения потока. Ламинарным называется движение жидкости, при котором ее частицы совершают упорядоченное движение и траектории частиц мало отличаются друг от друга, так что жидкость рассматривается как совокупность отдельных слоев, движущихся с разными скоростями, не перемешиваясь друг с другом. Ламинарное движение может быть как установившимся, так и неустановившимся. Открывая кран больше, увеличивая тем самым скорость, струйка приобретает некоторый волнистый характер, и местами струйка может иметь разрывы. Следовательно, в этот промежуток времени будет происходить нарушение струйчатого движения воды, чему соответствует некоторая средняя скорость При дальнейшем увеличении скорости потока в трубе струйка раствора исчезает. Частички этой струйки начинают перемешиваться с потоком воды. Частички раствора движутся в разном произвольном направлении, и при этом не наблюдается определенной закономерности их движения. Они имеют различные перемещения по пути движения. В результате перемешивания частиц вся масса воды, движущейся в трубе, становится несколько окрашенной. Такое движение можно считать беспорядочным. Переход движения потока в такое состояние происходит, когда скорость достигнет некоторой величины Движение, при котором наблюдается беспорядочный характер движения частичек жидкости по весьма сложным траекториям, является турбулентным движением, от латинского слова turbulentus - вихревой, беспорядочный. Турбулентным называется движение жидкости, при котором ее частицы совершают неустановившиеся и неупорядоченные движения по достаточно сложным траекториям, в результате этого происходит интенсивное перемешивание различных слоев жидкости (рис. 4.2).
Рис. 4.2. Движение жидкости в трубе: а - ламинарное; б - неустойчивое (неупорядоченное); в - турбулентное Турбулентное движение является неустановившимся движением. Турбулентный режим наблюдается при больших скоростях, когда средняя скорость Таким образом, ламинарное движение в трубе имеет место, когда В пределах Малейшее возмущение потока приводит к переходу неустойчивого ламинарного режима в турбулентный. Возмущение может произойти в результате некоторого сотрясения трубы в виде толчка, наличия в потоке тела, находящегося в состоянии колебания, и т.д. О. Рейнольдc на основании результатов опытов и использования размерностей физических величин установил, что величина критической скорости прямо пропорциональна динамической вязкости
где Этот коэффициент Нижней критической скорости Число Рейнольдса
Опыты, проведенные Рейнольдсом, подтвердили аналитические рассуждения, что ламинарный режим имеет место при На основании опытов Рейнольдса и многочисленных исследований других ученых для круглых труб критическое число Рейнольдса лежит в пределах Как было установлено опытами, вполне развитое турбулентное движение имеет место при Число Рейнольдса, являясь безразмерной величиной, одинаково для всех жидкостей и газов, а также диаметров трубопроводов. Однако для разных жидкостей и газов будут иметь место соответствующие критические скорости. В случае одинаковых диаметров труб и разных жидкостей критические скорости пропорциональны кинематическим вязкостям
Таким образом, при определении режима движения жидкости в трубопроводе необходимо знать его диаметр, вязкость жидкости и среднюю скорость. Вычислив число Рейнольдса, сравнивают его с критическими значениями Экспериментами, проведенными Рейнольдсом, а также многочисленными данными, полученными разными учеными, было установлено, что гидравлические потери напора Разность показаний пьезометров - потери напора по длине
На основании опытных данных был построен график
Рис. 4.3. Определение потерь напора по длине трубы
Рис. 4.4. Зависимость потерь напора по длине от скорости В зоне в, где
где В зоне в показатель степени с увеличением скорости изменялся от 1,75 до 2. Между ламинарной и турбулентной зонами находится зона б неустойчивого движения, где За интервал времени может наблюдаться как упорядоченное (струйчатое) движение, так и беспорядочное, т.е. в этой области жидкость находится в промежуточном неустойчивом состоянии. В этой зоне не удалось получить функциональную зависимость Для турбулентного движения при больших скоростях и числах Рейнольдса показатель степени
Коэффициент В учитывает размеры трубы и ее внутреннюю шероховатость поверхности, вид жидкости, ее плотность и вязкость. При показателе степени в пределах ♦ Пример 4.1 Определить критическую скорость, отвечающую переходу от ламинарного режима движения к турбулентному, для трубопровода диаметром По таблице П 1.3 приложения находим кинематическую вязкость веществ: вода - минеральное масло - воздух - Считаем, что переход от ламинарного режима движения к турбулентному происходит при
Для воды Для масла Для воздуха

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
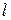 распределяются равномерно или достаточно равномерно. Потери напора (удельной механической энергии) по длине потока, затрачиваемые на преодоление сопротивления трения при равномерном или плавно изменяющемся неравномерном движении, называют потерями напора по длине и обозначают через
распределяются равномерно или достаточно равномерно. Потери напора (удельной механической энергии) по длине потока, затрачиваемые на преодоление сопротивления трения при равномерном или плавно изменяющемся неравномерном движении, называют потерями напора по длине и обозначают через  .
. .
.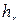 .
. , (4.1)
, (4.1) - сумма местных потерь напора.
- сумма местных потерь напора. влияет характер движения потока жидкости. Например, характер течения воды в равнинной и горной реках существенно различается, а траектории движения частиц жидкости в них кардинально различны.
влияет характер движения потока жидкости. Например, характер течения воды в равнинной и горной реках существенно различается, а траектории движения частиц жидкости в них кардинально различны. , частично находящейся в баке. В начале трубы имелся мундштук 3 (патрубок) с плавным переходом с большого входного отверстия на отверстие трубы. На конце трубы за пределами бака находился кран 4, с помощью которого можно было регулировать расход воды и среднюю скорость в стеклянной трубе
, частично находящейся в баке. В начале трубы имелся мундштук 3 (патрубок) с плавным переходом с большого входного отверстия на отверстие трубы. На конце трубы за пределами бака находился кран 4, с помощью которого можно было регулировать расход воды и среднюю скорость в стеклянной трубе  .
.
 . Одновременно пускался из резервуара 5 раствор краски, который выходил из трубочки 6 в трубу 2.
. Одновременно пускался из резервуара 5 раствор краски, который выходил из трубочки 6 в трубу 2. . Скорость
. Скорость  будет иметь место нарушение струйчатого течения, и поток в трубе будет находиться в неустойчивом состоянии. Такой режим движения является неустойчивым.
будет иметь место нарушение струйчатого течения, и поток в трубе будет находиться в неустойчивом состоянии. Такой режим движения является неустойчивым.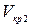 . Эта скорость называется верхней критической скоростью.
. Эта скорость называется верхней критической скоростью.
 , при этом происходит интенсивное перемешивание частиц в потоке жидкости.
, при этом происходит интенсивное перемешивание частиц в потоке жидкости.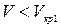 , турбулентное -
, турбулентное -  , движение является неустойчивым ламинарным движением.
, движение является неустойчивым ламинарным движением. и обратно пропорциональна плотности жидкости
и обратно пропорциональна плотности жидкости  и диаметру трубы
и диаметру трубы 
 - кинематическая вязкость,
- кинематическая вязкость,  ;
;  - безразмерный эмпирический коэффициент, соответствующий
- безразмерный эмпирический коэффициент, соответствующий 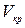 .
. , а верхней критической скорости
, а верхней критической скорости  .
. . (4.3)
. (4.3) , турбулентный режим, если
, турбулентный режим, если  .
. . Для практических инженерных расчетов было принято значение
. Для практических инженерных расчетов было принято значение  . Ламинарный режим устанавливается, когда
. Ламинарный режим устанавливается, когда  , т.е.
, т.е.  , и числу
, и числу 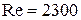 соответствует критическая скорость
соответствует критическая скорость  . Это значение можно принять за
. Это значение можно принять за  ). При
). При  будет неустойчивый (неупорядоченный) режим движения, т.е. переходная неустойчивая критическая область течения жидкости.
будет неустойчивый (неупорядоченный) режим движения, т.е. переходная неустойчивая критическая область течения жидкости. . (4.4)
. (4.4) . Опыты заключались в следующем. На трубе диаметром
. Опыты заключались в следующем. На трубе диаметром  ,
,  .
. . (4.5)
. (4.5) . (4.6)
. (4.6)

 , (4.7)
, (4.7) - некоторый размерный коэффициент;
- некоторый размерный коэффициент; 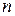 - показатель степени.
- показатель степени. . В этой области струйчатое движение нарушается, как и неустойчиво гидравлическое сопротивление.
. В этой области струйчатое движение нарушается, как и неустойчиво гидравлическое сопротивление.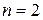 . Это область квадратичного сопротивления:
. Это область квадратичного сопротивления: . (4.8)
. (4.8) движение жидкости будет происходить в области доквадратичного сопротивления.
движение жидкости будет происходить в области доквадратичного сопротивления. мм при движении в нем воды, минерального масла и воздуха при их температуре
мм при движении в нем воды, минерального масла и воздуха при их температуре  20°.
20°. м2/с;
м2/с; м2/с;
м2/с; м2/с
м2/с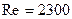 .
.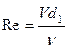 ,
,  .
. м/с.
м/с. м/с.
м/с. м/с.
м/с.