
|
|
ТЕОРЕМА ИЗМЕНЕНИЯ КОЛИЧЕСТВА ДВИЖЕНИЯ ДЛЯ ПОТОКА ЖИДКОСТИПри решении некоторых гидравлических задач использования уравнения Бернулли недостаточно, и в этих случаях применяется теорема об изменении количества движения материальной точки. Количеством движения материальной точки называется произведение ее массы Тело массой Изменение количества движения
За этот промежуток времени на тело будет действовать импульс сил
Теорема количества движения сформулирована следующим образом. Изменение количества движения материальной точки за некоторый промежуток времени равно сумме импульсов сил, приложенных к точке, за этот же промежуток времени,
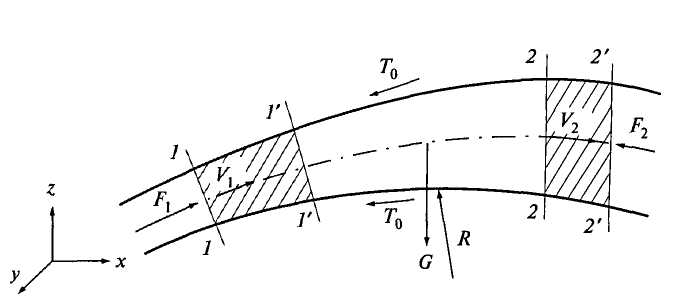
Теорема количества движения называется также теоремой импульсов. Применим данную теорему к участку потока между сечениями 1-1 и 2-2 при установившемся движении потока жидкости расходом
Масса элементов участков 1-1' и 2-2' на рисунке заштрихованы. Так как стенки потока непроницаемы, то согласно уравнению неразрывности массы этих элементов одинаковы:
Масса, проходящая через сечения,
Рис. 3.12. К теореме количества движения для потоков жидкости Если в живом сечении местные скорости в разных его точках различны, то количество движения
где При предположении, что скорости во всех точках живого сечения равны средней скорости
Коэффициент Буссинеска - отношение фактического количества движения к условному Количество движения, выраженное через среднюю скорость,
Для турбулентных потоков на основании опытных исследований На практике при решении гидравлических задач обычно коэффициент Буссинеска не учитывается, т.е. принимается Средние скорости в сечениях равны
Изменение количества движения
Относительно оси
Рассмотрим все внешние силы и импульс, действующие на объем жидкости • Силы давления, действующие на торцы сечений 1-1 и 2-2,определяются силами
• Сила тяжести выделенного объема жидкости
• Силы реакции боковых стенок, ограничивающих рассматриваемый объем жидкости, равны
• Сила внешнего трения, воздействующая на внутренние стороны боковых стенок, -
Таким образом, импульс на ось
Уравнение изменения количества движения в гидравлической форме согласно (3.102) и (3.107) имеет следующий вид:
Уравнение изменения количества движения в гидравлическом виде можно сформулировать следующим образом. Изменение количества движения потока жидкости при переходе от плоского живого сечения 1-1 к плоскому живому сечению 2-2 за единицу времени относительно выбранной координатной оси равно сумме проекции внешних сил на ось, действующих на объем жидкости между сечениями 1-1 и 2-2.
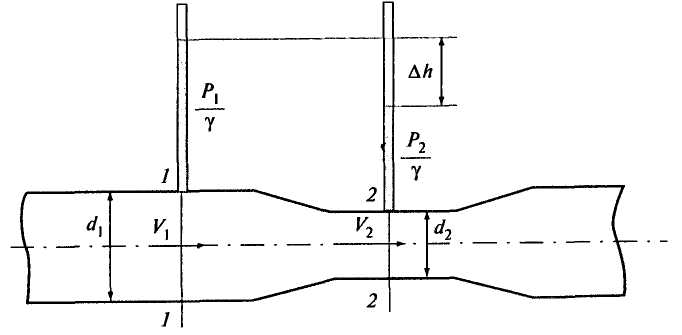
НЕКОТОРЫЕ ПРИЛОЖЕНИЯ УРАВНЕНИЯ БЕРНУЛЛИ Расходомер Вентури Расходомер Вентури представляет собой плавно суженную и расширяющуюся цилиндрическую вставку, устанавливаемую в трубе. Чтобы понять принцип его работы, рассмотрим рис. 3.13. Установим два пьезометра: один в расширенной части расходомера, другой - в сужении. Приведенные далее рассуждения должны показать, что при изменении расхода жидкости, проходящей по трубопроводу, меняется разность показаний пьезометров
Рис. 3.13. Расходомер Вентури Напишем уравнение Бернулли для сечений 1-1 и 2-2, полагая отсутствие потерь напора,
Поскольку
Разность показаний пьезометров составляет
Подставив выражение (3.110) в уравнение (3.109), получим
Поскольку площади поперечных сечений 1-1 и 2-2 известны, то, используя уравнение неразрывности для несжимаемой жидкости, имеем
или
Подставив полученное выражение для
Теоретический расход жидкости в трубопроводе составляет
или
где
Таким образом, если известны диаметр трубы и диаметр сужения и измерена разность пьезометрических высот, то можно вычислить расход жидкости, проходящей по трубопроводу по формуле (3.113). Следует отметить, что в случае движения идеальной жидкости приведенные ранее рассуждения правильны. При движении через расходомер вязкой жидкости возникают потери напора, поэтому необходимо ввести в конечную формулу соответствующую поправку на сопротивление в виде коэффициента расхода водомера Коэффициент расхода водомера Вентури, изготовленного в соответствии со стандартом по измерению расхода жидкостей, составляет Окончательная формула с учетом
где 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 на скорость ее движения
на скорость ее движения 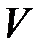 . Количество движения
. Количество движения 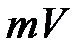 является вектором, направление которого совпадает с направлением движения, т.е. со скоростью. Количество движения, зависящее от массы и ее скорости, является мерой механического движения. Понятие количества движения (КД) положено в основу механики Ньютона.
является вектором, направление которого совпадает с направлением движения, т.е. со скоростью. Количество движения, зависящее от массы и ее скорости, является мерой механического движения. Понятие количества движения (КД) положено в основу механики Ньютона.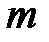 под действием сил переместится в другое положение за определенное время
под действием сил переместится в другое положение за определенное время 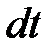 , и скорость тела изменится
, и скорость тела изменится 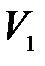 до
до 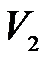 .
.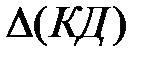
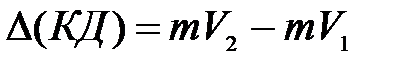 . (3.92)
. (3.92)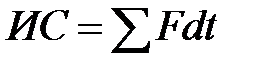 . (3.93)
. (3.93)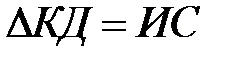 :
: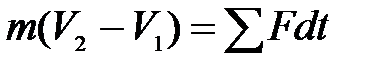 . (3.94)
. (3.94)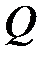 в определенный промежуток времени (рис. 3.12). За время
в определенный промежуток времени (рис. 3.12). За время 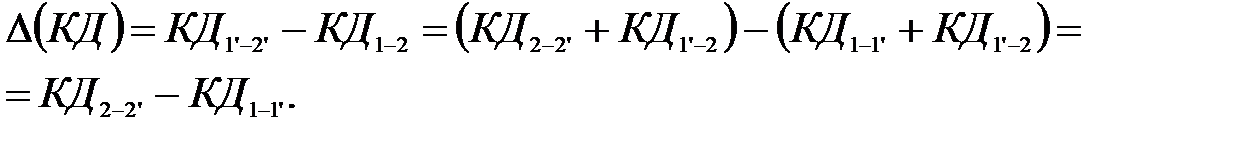 (3.95)
(3.95)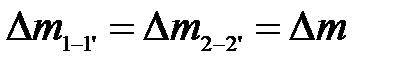 . (3.96)
. (3.96) .
.
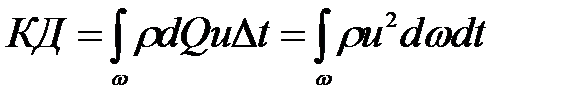 , (3.97)
, (3.97) - скорость в определенной точке сечения, местная скорость.
- скорость в определенной точке сечения, местная скорость.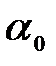 (коэффициент количества движения)
(коэффициент количества движения)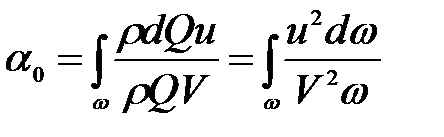 . (3.98)
. (3.98) .
.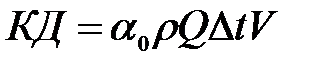 . (3.99)
. (3.99) .
. .
.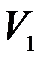 , и
, и  , тогда количество движений для массы элементов участков:
, тогда количество движений для массы элементов участков: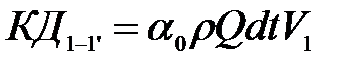 ;
;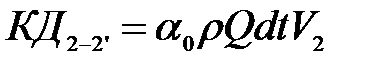 . (3.100)
. (3.100) . (3.101)
. (3.101)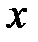
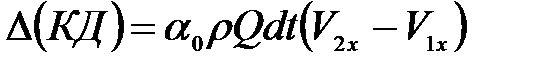 . (3.102)
. (3.102)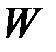 , находящийся между сечениями 1-1 и 2-2.
, находящийся между сечениями 1-1 и 2-2.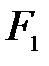 и
и  . Проекция импульса сил давления на ось
. Проекция импульса сил давления на ось 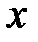
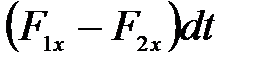 . (3.103)
. (3.103)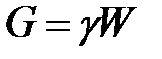 . Проекция импульса сил давления на ось
. Проекция импульса сил давления на ось 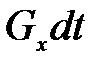 . (3.104)
. (3.104)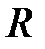 . Проекция импульса сил реакций стенок на ось
. Проекция импульса сил реакций стенок на ось 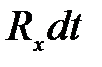 . (3.105)
. (3.105)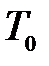 . Проекция импульса сил внешнего трения на
. Проекция импульса сил внешнего трения на  . (3.106)
. (3.106)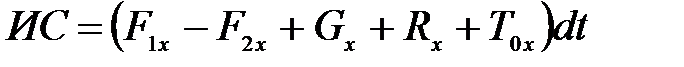 . (3.107)
. (3.107)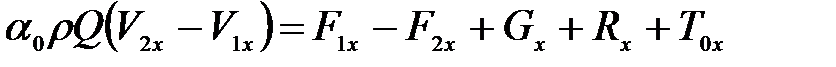 . (3.108)
. (3.108)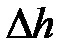 .
.
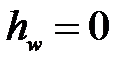 :
: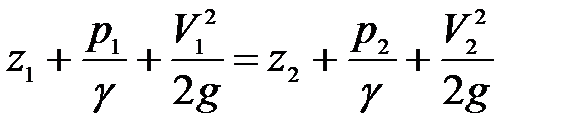 . (3.109)
. (3.109)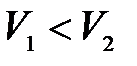 , следовательно, показания пьезометра в первом сечении будут больше, чем во втором:
, следовательно, показания пьезометра в первом сечении будут больше, чем во втором: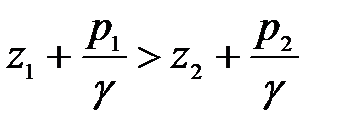 .
.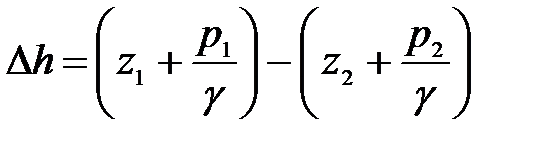 . (3.110)
. (3.110)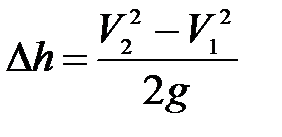 . (3.111)
. (3.111)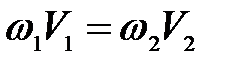 ,
,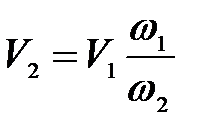 .
.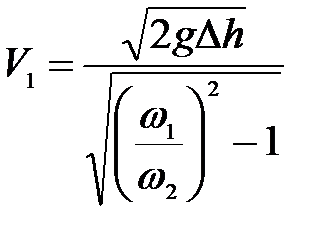 . (3.112)
. (3.112)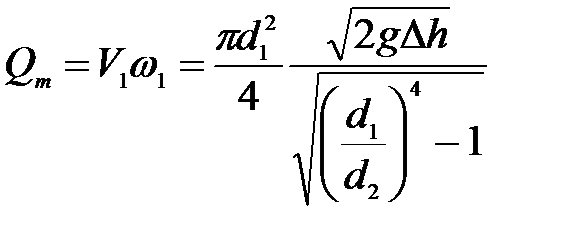 . (3.113)
. (3.113)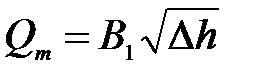 ,
, - постоянная расходомера.
- постоянная расходомера. . (3.114)
. (3.114)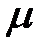 ,
, 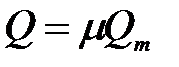 .
.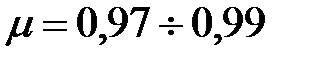 .
.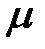
 , (3.115)
, (3.115)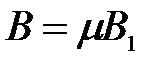 - окончательная постоянная водомера, имеющего конкретные значения
- окончательная постоянная водомера, имеющего конкретные значения 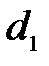 и
и 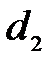 .
.