
|
|
РАСЧЕТ СЛОЖНОГО (РАЗВЕТВЛЕННОГО) НЕЗАМКНУТОГО ТРУБОПРОВОДА (ТРУБОПРОВОДНОЙ СЕТИ)12 Различают следующие виды сложного трубопровода: а) незамкнутый, или, иначе, тупиковый (рис. 5-18); б) замкнутый, или, иначе, кольцевой (рис. 5-19). В этом параграфе рассмотрим расчет незамкнутого сложного трубопровода (тупиковой водопроводной сети), питаемого из бака Б, установленного на водонапорной башне (рис. 5-18). Такой трубопровод состоит из магистрали (главной линии; см., например, линию 1—2 — 3 — 4) и ответвлений (линий второго порядка; см. линии 2 — 5 и 3 — 6).
Рис. 5-18. Тупиковая (незамкнутая) водопроводная сеть Р – река (источник водоснабжения), К — береговой колодец, С - насосная станция, Б — водонапорная башня, I — самотечная труба, II — всасывающая труба, III — напорная труба, 1 — 2 — 3 — 4 – магистраль, 2 — 5 и 3 — 6 — ответвления. Потери напора: hc — в трубе I, hBC — в трубе II, hH — в трубе III 1°. Случай, когда высотное положение водонапорного бака не задано. Для гидравлического расчета рассматриваемой сети труб должны быть заданы: а) длины l отдельных труб и начертание сети их на плане местности в горизонталях; б) расчетные расходы воды, забираемые в отдельных точках сети: q4, q5, q6; в) расход q’ забираемый с 1 м длины того или другого трубопровода (см.трубопровод 2 – 5); г) минимально допустимые отметки горизонтов воды в воображаемых пьезометрах, привключенных к концевым точкам сети (точкам 4, 5, 6):
Рис. 5-19. План замкнутой (кольцевой) сети Б — водонапорная башня В результате гидравлического расчета можем найти: диаметры труб, а также отметку горизонта воды в водонапорном баке, обеспечивающую подачу заданных расходов воды в заданные точки сети. Общий ход расчета может быть намечен следующий. 1.Устанавливаем расчетные расходы для отдельных участков сети. Расчетный расход какого-либо участка сети должен равняться сумме расходов, забираемых из сети ниже (по течению) этого участка. Например, расчетный расход для участка 3 — 4
расчетный расход для участка 1—2
расчетный расход для участка 2—5 согласно формуле (5-97) будет
2.Выбираем линию трубопроводов, которую следует рассматривать как магистральную. В качестве магистрали намечаем линию: наиболее нагруженную расходами, наиболее длинную, характеризуемую наибольшими отметками поверхности земли. Если магистраль будет намечена неудачно, то в конце расчета получим некоторую неувязку (см. ниже), причем расчет придется выполнять заново, задавшись новым направлением магистрали. Расчет магистрали 1 — 2 — 3 — 4 1.Задаемся для отдельных участков магистрали так называемой экономической скоростью D, м . . . . . . . . . . . . . . . . 0,10 0,20 0,25 0,30
2.Установив скорости для отдельных участков магистрали, находим диаметры труб магистрали:
полученное значение D' округляем до ближайшего (большего или меньшего) сортаментного значения D. 3. Зная для каждой трубы ее диаметр D и расход Q, определяем для всех участков магистрали потери напора по формуле:
4.Имея величины hl для отдельных участков магистрали, строим пьезометрическую линию Р — Р (рис. 5-18). Построение этой линии начинаем с конца магистрали, зная отметку Определение отметки Построив пьезометрическую линию, легко можем написать следующую зависимость, по которой и определяем отметку
где Отметка Поясним понятие экономической скорости, о которой говорилось выше. Положим, что мы имеем магистраль, выполненную из труб определенного диаметра. Представим теперь, что этот диаметр постепенно уменьшается. При этом получаем следующее: скорости в магистральных трубах возрастают; потери напора в этих трубах растут; высота водонапорной башни HБ увеличивается; увеличивается также и высота Н подъема воды насосами,1 а следовательно, растет и мощность N насосов, зависящая от QH0, где Н0 = Н + hc + hвс + hн (см. рис. 5-18). Можно утверждать, что с уменьшением диаметра труб магистрали стоимость самой магистрали будет уменьшаться; стоимость же водонапорной башни и насосной станции будет увеличиваться; также будет увеличиваться и ежегодный расход электрической энергии на насосной станции (в связи с работой более мощных насосов). При увеличении диаметра труб магистрали получаем обратную картину: стоимость самой магистрали растет, а стоимость башни и насосной станции (а также электроэнергии) уменьшается. На основании сказанного был исследован вопрос о том, при каких именно скоростях в магистрали получается наиболее экономичное сооружение; в результате и были установлены величины приведенных выше так называемых экономических скоростей. Расчет ответвлений Построив пьезометрическую линию для магистрали, мы тем самым задали напоры в начале каждого ответвления. Например, напор в начале ответвления 3—6 определяется отметкой В связи с этим обстоятельством расчет ответвлений принципиально отличается от расчета магистрали: а) в случае магистрали напор в начале ее не был задан (отметка не была задана); поэтому при расчете магистрали мы исходили из скорости б) в случае ответвлений напор в начале их задан; задан также и напор в конце каждого ответвления; поэтому при расчете ответвлений исходим из заданной потери напора для каждого ответвления (разности напоров в начале и в конце ответвления). Имея в виду сказанное, поступаем следующим образом (см. рис, 5-20, на котором для примера представлен продольный профиль по ответвлению 3-6): а) определяем потерю напора в ответвлении:
где б) переписываем формулу (5-2), служащую для определения потерь напора, в виде:
по этой формуле находим К' в)по соответствующим таблицам, зная К' находим диаметр D'; полученное значение D' округляем до ближайшего большего сортаментного значения D г)по найденному значению D определяем модуль К и вычисляем; действительные потери напора в ответвлении hl. Как видно из чертежа, благодаря округлению D' до большего значения D потеря напора в ответвленщ/уменьшилась, причем пьезометрическая линия несколько поднялась; при округлении D' до меньшего сортаментного значения отметка
Рис. 5-20. Ответвление незамкнутой сети
Рис. 5-21. К расчету магистрали при заданной высоте водонапорной башни В заключение приведем следующее указание. Если бы в начале расчета мы выбрали магистраль неудачно, то при расчете того или другого ответвления у нас получилось бы соотношение (см. пример ответвления 3-6 на рис. 5-20): 2°. Случай, когда высотное положение водонапорного бака задано.Ограничимся рассмотрением только магистральной линии (рис. 5-21). Положим, что для расчета имеются следующие исходные данные: а) длины труб l1, l2 ...; б) расходы воды в отдельных трубах Q1, Q2, …; в) потеря напора Z в рассматриваемом трубопроводе. В результате расчета требуется найти диаметры труб: D1, D2, D3, …. Ход расчета 1.Обозначив через L длину магистрали:
2. Находим для каждого участка значение К (в первом приближении):
3. Исходя из найденных К, по таблице, выражающей зависимости К =f(D) определяем: а) ближайшие меньшие сортаментные значения диаметра труб: D'1 , D'2, D'3, ... б) ближайшие большие сортаментные значения диаметра труб: D”1 , D”2, D”3, ... 4. Рассматриваем различные комбинации найденных сортаментных диаметров, например: 1-й вариант: D'1 , D”2, D’3, D”4 и т. д.; 2-й вариант: D"1, D'2 ,D”3, D’4 и т. д. Если число отдельных участков магистрали равно n , то число возможных комбинаций (вариантов) будет 2n. Из этого числа вариантов по техническим соображениям мы должны отобрать только те из них, которые удовлетворяют условию: ∑ hl ≤ Z, где ∑ hl - cумма потерь напора для всех участков магистрали. Очевидно, варианты, характеризуемые условием ∑ hl > Z неприемлемы, так как в них при заданном Z требуемые расходы Q не будут обеспечиваться. 5. Из числа отобранных вариантов останавливаемся (по экономическим соображениям) , для которого масса трубопровода (т. е. величина ∑(lβ), где β - масса 1 м трубы данного диаметра) оказывается минимальной. Ясно, что трубопровод, имеющий наименьшую массу, будет иметь также и наименьшую стоимость. § 5-12. ЗАМЕЧАНИЯ О РАСЧЕТЕ СЛОЖНОГО ЗАМКНУТОГО ТРУБОПРОВОДА Поясним только основной принцип расчета сложного замкнутого трубо-провода (кольцевой водопроводной сети). Рассмотрим сеть, имеющую одно кольцо (рис. 5-22, а). Если расходы воды забираются в точках 4 и 5 сети, как показано на чертеже, то направление движения воды во всех трубах, кроме трубы 4—5, нам известно заранее.
Положим, что для расчёта нам заданы: а) длины всех труб; б) отметка горизонта воды в водонапорном баке, расположенном в точке 1; в) минимальные допустимые отметки горизонта воды в воображаемых пьезометрах, присоедененных к узловым точкам сети 3,4, 5, 6; г) расходы q4 и q5, забираемые из сети. Требуется установить диаметры отдельных труб, а также построить пьезометрическую линию для трубопровода. Первую задачу (определение диаметров труб) решаем путем ряда попыток. 1-я попытка. Задаемся: а) диаметрами отдельных труб; б) направлением движения воды в трубе 4 — 5, например, слева направо; в) распределением расхода q5 между линиями 4 — 5 и 6—5; здесь считаем, что расход линии 4 — 5 равен εq5, а расход линии 6 — 5 равен (1 — ε) q5, причем задаемся величиной ε. В рассматриваемом кольце труб имеются два разных потока: один против часовой стрелки (2 — 3 — 4), другой – по часовой стрелке (2 — 6 —5). Задавшись направлением движения воды по линии 4 — 5 слева направо, мы тем самым назначим встречу двух указанных потоков в точке 5. Точка встречи двух потоков называется точкой водораздела или нулевой точкой. Чтобы проверить, правильно ли мы задались диаметрами труб, положением точки водораздела и величиной ε , поступаем следующим образом. Мысленно разрезаем наше кольцо по намеченной точке водораздела, причем получаем сеть, изображенную на рис. 5-22,б. Далее по обычным формулам подсчитываем потерю напора для линии 1- 2 - 3 - 4 - 5' (h1-2-3-4-5') и для линии 1- 2 - 6 - 5" (h1-2-6-5"). После этого сопоставляем между собой две найденные потери напора. Если (hl)1-2-3-4-5' = (h1)1-2-6-5" , то заключаем, что напоры в точках 5' и 5" будут одинаковыми, что и должно быть, поскольку точки 5' и 5" представляют собой физически одну точку 5 (рис. 5-22, а). Следовательно, получив указанное равенство, можем утверждать, что выше мы задались правильно как диаметрами труб D), так и величиной ε. Если указанное равенство не получается, то приходится изменять величины D и ε, а иногда и переносить точку водораздела в другую точку сети (в точку 4 на чертеже). При этом обращаемся ко 2-й, 3-й и последующим Попыткам, добиваясь того, чтобы приведенное выше равенство было выдержано хотя бы приближенно. МАТЕРИАЛЫ ПРАКТИЧЕСКИХ ЗАНЯТИЙ ПО РАСЧЕТАМ НАПОРНЫХ ТРУБОПРОВОДОВ 1°. Задачи на расчет коротких трубопроводов. № 1. Имеем простой трубопровод постоянного диаметра (см. рис. 5-3,б). Истечение воды из сосуда А по этому трубопроводу происходит в атмосферу. Дано: Q = 40 л/с; l = 25 м; D = 150 мм. Требуется найти напор H. Ответ. Н = 3,8 м. № 2. Два резервуара А и В, наполненные водой, соединены трубопроводом постоянного диаметра. На трубопроводе имеется задвижка Лудло С с открытием a/D = 0,5 (рис. 5-23).
Рис. 5-23. К задаче № 2 Дано: Q = 30 л/с; l = 25 м; наибольшая допустимая разность горизонтов воды в резервуарах Zмакс = 2,0 м. Требуется определить диаметр трубопровода D. Решение. Для расчета пользуемся основной зависимостью (5-36'):
В этой формуле ω = f1/(D) и µт = f2(D), в связи с чем найти непосредственно диаметр D из уравнения (А) нельзя. Это уравнение приходится решать в отношении D подбором.2 С этой целью переписываем (А) в виде:
величина
следовательно, искомая величина D должна удовлетворять условию
Рис. 5-24. К задаче № 2 Так как при истечении под уровень [см. формулу 5-37]
причём ζвх = [см. формулу (4-163)], ζвых = 1,0 [см. формулу (4-135)] и ζ3 = 5,3 см. формулу 4-15, стр. 199, то
По полученной зависимости (Д) вычисляем величины µтω, задаваясь различными сортаментными диаметрами трубы. Все вычисления сводим в таблицу (форма 1). По данным 1-й и 7-й строк таблицы (форма 1) строим на рис. 5-24 график µтω = f(D). Откладываем по вертикальной оси этого графика величину (В), определяем диаметр D, отвечающий Zmakc. Полученное таким образом D округляем до ближайшего большего сортаментного значения, т. е. до D = 150 мм. Форма 1
№3. Вода из бака A поступает в открытый резервуар В по трубопроводу, состоящему из труб разного диаметра (рис. 5-25).1 Д а н о (см. чертёж): избыточное (сверхатмосферное) поверхностное давление в баке А равно p1 = 120 кПа ( = 102 кгс/см2); НА = 1,0 м; НВ = 5,0 м; l1 = 20,0 м; l2 = 30,0 м; D1 = 150 мм; D2 = 200 мм. Требуется найти расход Q и построить напорную и пьезометрическую линии для трубопровода. Р е ш е н и е. Напор Z, под которым вода движется из резервуара А в резервуар В (см. рис. 5-25),
Рис. 5-25. К задаче №3 Поскольку в нашем случае имеет место истечение под уровень, для расчёта пользуемся формулой (5-36), которую перепишем в виде:
где
В нашем случае полный коэффициент сопротивления
Причём все коэффициенты должны быть приведены к одной и той же скорости, согласно зависимостям (5-20) – (5-23). Поскольку в формулу для расхода Q мы ввели вместо ω площадь сечения первой трубы ω1, то указанные коэффициенты сопротивления ζ1 и ζ2 должны приводиться к скорости υ1. Имея в виду сказанное, для коэффициентов ζ1 , ζ2 , ζр.р и ζвых принимаем следующие зависимости:
Полный коэффициент сопротивления
Найдём величины λ и ζ, входящие в уравнение (И): a) величина λ1 для чугунной трубы, бывшей в эксплуатации, диаметром D=150мм, согласно табл. 5-3 (с.212), λ1 = 0,0356; б) величина λ2 для такой же трубы, но диаметром D=200мм, λ2 = 0,0323; в) величина ζвх для входа в трубу из бассейна больших размеров, согласно (4-163), ζвх = 0,5; г) ζвых для выхода в бассейн больших размеров, согласно формуле (4-135), ζвых = 1,0; Находим, согласно формуле (И), величину ζf и, согласно формулам (Е) и (Ж), величины µТ и Q:
Для построения напорной линии Е – Е вычисляем отдельные потери напора:
По этим данным строим линию Е – Е , показанную на рис. 5-25. Пьезометрическую линию Р – Р проводим ниже напорной на величину 2°. Задачи на расчёт длинных трубопроводов. №4. На рис. 5-11 представлен длинный трубопровод, состоящий из труб разного диаметра. Трубопровод соединяет два резервуара А и В. Дано рис. 5-11: Z = 9,0 м; l1 = 1200; l2 = 1500 м; l3 = 1000 м; D1= 200 м; D2= 250 м; D3=200 м; Требуется найти расход воды Q. Ответ: Q =20 л/с. №5. Вода из бака вытекает через длинную трубу постоянного диаметра в атмосферу. В конце трубы имеется сопло (см. рис. 5-12). Дано: Q =40 л/с, l = 900 м, Н = 22 м; площадь поперечного сечения сопла ω0 = 0,003м2; коэффициент расхода сопла µсп = 0,92. Требуется найти диаметр трубы D. Решение. Для расчета пользуемся зависимостью (5-77):
Из этой зависимости находим модуль расхода:
Зная К, по табл. 5-3 (см. стр. 212) находим диаметр трубопровода D — 200 мм. Как видно, в качестве такого диаметра мы приняли сортаментный диаметр, дающий ближайшую к установленной выше величину К,
СПИСОК ЛИТЕРАТУРЫ 5-1. Абелев А. С. Сельскохозяйственное водоснабжение и основы гидравлики.—Л.; Сельхозгиз, 1959. 5-2. Абрамов Н. Н., Поспелова М. М. Расчет водопроводных сетей.— М: Госстрой-издат, 1962. 5-3. Андрияшев М. М. Гидравлический расчет водопроводных сетей.—М.: Строй-издат, 1964. 5-4. Мошнин Л. Ф. Методы технико-экономического расчета водопроводных сетей.— М.: Госстройиздат, 1950. 5-5. Симаков Г. В. Сифонные водосбросы (пособие к курсовому и дипломному проектированию). — Л.: из-дво ЛПИ им. М. И. Калинина, 1974. 5-6. Шевелев Ф. А. Таблицы для гидравлического расчета стальных, чугунных, асбестоцементных и пластмассовых водопроводных труб.—М.: Строй-издат, 1970 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

 . Задавая,
. Задавая,  ).
).




 (пояснение понятия скорости иэк см. в следующем пункте); эта скорость может быть принята равной
(пояснение понятия скорости иэк см. в следующем пункте); эта скорость может быть принята равной  1,0 м/с; вообще же говоря, данная скорость должна изменяться с изменением диаметра труб:
1,0 м/с; вообще же говоря, данная скорость должна изменяться с изменением диаметра труб:

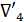 . Идя от точки n (см. чертеж) против течения и откладывая по вертикали вверх найденные величины (hl)3-4, (hl)2-3, (hl)1-2 получаем искомую линию Р — Р.
. Идя от точки n (см. чертеж) против течения и откладывая по вертикали вверх найденные величины (hl)3-4, (hl)2-3, (hl)1-2 получаем искомую линию Р — Р. горизонта воды в водонапорном баке. Пояснение понятия экономической скорости.
горизонта воды в водонапорном баке. Пояснение понятия экономической скорости. :
:
 — потери напора по длине всей магистрали.
— потери напора по длине всей магистрали. ; напор в начале ответвления 2-5 определяется отметкой
; напор в начале ответвления 2-5 определяется отметкой  .
.
 ;
; в точке 6 оказалась бы не обеспеченной.
в точке 6 оказалась бы не обеспеченной.

 , …, вычисляем средний пьезометрический уклон:
, …, вычисляем средний пьезометрический уклон:
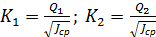 и т.д.
и т.д.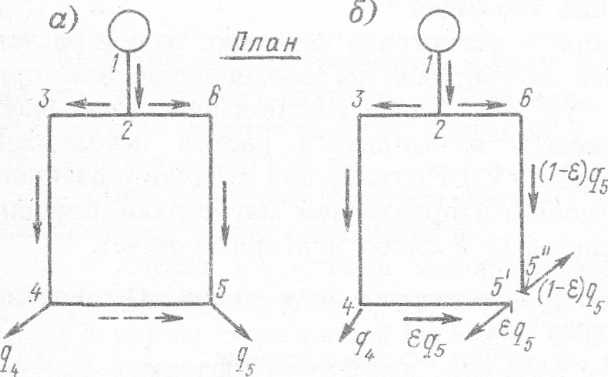

 (А)
(А) (Б)
(Б) (В)
(В)
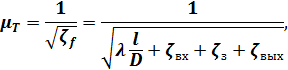
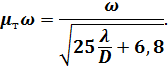
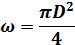






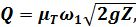 (Е)
(Е)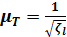 (Ж)
(Ж) (З)
(З)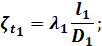


 (И)
(И)
 .
.




 = 1,35м для первой трубы и на величину
= 1,35м для первой трубы и на величину  = 0,43 м для второй трубы (считаем α = 1,0).
= 0,43 м для второй трубы (считаем α = 1,0).
