
|
|
Приборы и оборудование: ИП – источник питания, ФПЭ-06 – модуль “Определение работы выхода”, PV – вольтметр (прибор Ф-214 1/2), PA – амперметр (прибор Ф-2141/4).
Методика измерений Измеряя на опыте зависимость тока насыщения от температуры (рис.13.2), можно определить работу выхода для данного металла. В нашем случае для определения работы выхода используется метод прямых Ричардсона. Прологарифмируем уравнение (13.3):
График зависимости
Экспериментальная установка
Амперметр на панели источника питания служит для контроля тока накала IН, максимальное значение которого не должно превышать 2.2 А. Плавная регулировка напряжения накала осуществляется ручкой, расположенной под амперметром. Напряжение накала UН измеряется вольтметром (PV), который подключается к тем клеммам на источнике питания, где указано напряжение 2,5–4,5 В. Вольтметр на панели источника питания измеряет анодное напряжение UА, регулировка которого осуществляется ручкой на панели источника питания, расположенной непосредственно под вольтметром. Для измерения анодного тока IА используется амперметр, который подключается к модулю ФПЭ-06 к клеммам РА. Он должен работать в режиме миллиамперметра, измеряя ток до 20 mA. Порядок выполнения работы 1. Подключить модуль ФПЭ-06 соединительным кабелем к источнику питания. 2. Установить напряжение накала UН равным 3.9 В, измерить и записать силу тока накала IH и, увеличивая анодное напряжение в интервале от 10 до 100 В через каждые 10 В, измерять значение анодного тока IА. Все результаты записать в табл. 13.1. Таблица 13.1
3. Провести измерения (пункт 2) для следующих значений напряжения накала UН: 4.2; 4.5; 4.8; 5.7 В. 4. Для каждого значения тока накала построить вольтамперную характеристику и точку перегиба полученной кривой считать точкой насыщения. 5. Для всех значений напряжения накала рассчитать мощность, выделяемую на катоде, по формуле: 6. По графику (рис. 13.6) зависимости температуры катода от расходуемой на его нагрев мощности определить температуру катода для каждого значения мощности нагрева. 7. Рассчитать плотность анодного тока насыщения по формуле 8. Все полученные данные занести в табл. 13.2. 9. Построить график зависимости
10. Определить тангенс угла наклона α полученной прямой к оси абсцисс: 11. Сделать выводы.
Таблица 13.2
Таблица 13.3
Контрольные вопросы
1. В чем заключается явление термоэлектронной эмиссии? Напишите формулу Ричардсона-Дэшмена, объясните ее смысл и характер выражаемой ею зависимости. 2. Чем определяется работа выхода электронов из металла в модели свободных электронов? 3. Каковы причины появления работы выхода электронов из металла? 4. Почему при обычных температурах (комнатных) из металла «испаряется» лишь малая доля свободных электронов? 5. Почему необходимо использовать методы статистической физики для объяснения термоэлектронной эмиссии? 6. Поясните, изменится ли представление о работе выхода, если применять не классическую электронную теорию, а квантовую. 7. Объясните, в чем заключается косвенный метод определения температуры катода.
Используемая литература [1] § 18.5; [3] §§ 5.10, 5.11, 5.12; [7] §§ 104, 105.
Лабораторная работа 3-14 Определение коэффициента линейного теплового расширения Цель работы: измерение температурного коэффициента линейного расширения металла.
Теоретическое введение Для объяснения зависимости теплоемкости твердых тел от температуры (модели Эйнштейна, Дебая) используется модель кристалла, в которой принимается, что отклонения атомов, ионов (частиц, из которых состоит кристалл) из положения равновесия малы по сравнению с расстояниями между ними. Предполагается, что можно точно определить свойства твердого тела, сохраняя в разложении потенциальной энергии кристалла лишь первый неисчезающий член, квадратичный по смещениям атомов. Это – так называемое гармоническое приближение. Предположение о малости колебаний кажется разумным для большинства твердых тел при температурах, лежащих гораздо ниже температуры плавления. Может показаться, что в том случае, когда выполняется предположение о малых колебаниях атомов кристалла, поправки к гармоническому приближению важны лишь в очень точных вычислениях. Тем не менее ряд свойств твердых тел, проявляющихся при любой температуре, не удается объяснить в чисто гармоническом приближении, поскольку они полностью обусловлены высшими (ангармоническими) членами в разложении энергии взаимодействия атомов вблизи ее равновесного значения. Важнейшее из этих физических свойств – эффект теплового расширения. У строго гармонического кристалла равновесные размеры не зависели бы от температуры. Для кристаллов с кубической симметрией коэффициент теплового расширения определяется так:
Здесь l – линейные размеры тела, V – его объем. Индекс «P» означает, что производная берется при постоянном давлении. При свободном тепловом расширении твердого тела тепловая деформация ε (относительное изменение линейных размеров) будет пропорциональна изменению температуры DT:
Как правило, с повышением температуры размеры твердых тел увеличиваются, т.е. α>0. Явление теплового расширения в твердых телах обусловлено некоторым изменением характера межатомного взаимодействия при изменении температуры. С усилением теплового движения, с увеличением температуры, с ростом амплитуды колебаний атомов твердого тела силы притяжения и отталкивания между ними, определяющие их энергию взаимодействия, различным образом меняются. И это приводит к тому, что среднее расстояние между атомами в твердом теле изменяется при изменении температуры. Поясним на простой модели линейной цепочки атомов причины теплового расширения. Для этого рассмотрим влияние ангармонического вклада в выражении для потенциальной энергии взаимодействия пар атомов при температуре T. Потенциальную энергию взаимодействия атомов при смещении на расстояние x от положения равновесия x0 представим в виде:
Здесь k – квазиупругая постоянная, g – ангармоническая постоянная; первое слагаемое – потенциальная энергия в гармоническом приближении, второе слагаемое – ангармонический вклад в потенциальную энергию. Он определяет асимметрию взаимного отталкивания атомов. В отсутствие ангармонизма (g=0) на атомы действует только квазиупругая сила – зависимость U(x) описывается параболой. Из (14.3) находим по определению (
Среднее по времени значение силы
Укажем, что, во-первых, по определению (14.2) Из соотношения (14.5) следует также, что с учётом ангармонизма:
Для нахождения величины
где kБ – постоянная Больцмана. Сравнивая (14.6) и (14.2) с учётом (14.7) находим, что для линейной цепочки атомов
Тогда
Экспериментальная часть Приборы и оборудование: исследуемый образец, нагреватель, термопара, индикатор, милливольтметр, линейка, термометр. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 (13.9)
(13.9) от
от  является прямой линией с угловым коэффициентом
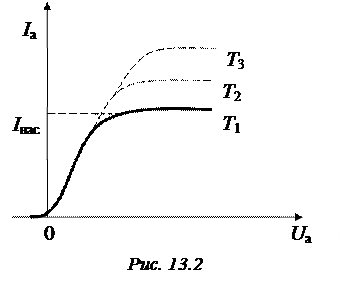
является прямой линией с угловым коэффициентом 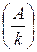 (рис.13.3). Определив тангенс угла α наклона прямой к оси абсцисс, можно найти работу выхода:
(рис.13.3). Определив тангенс угла α наклона прямой к оси абсцисс, можно найти работу выхода: . (13.10)
. (13.10)
 Электрическая схема для проведения опыта представлена на рис. 13.4 и 13.5. В качестве диода в работе используется радиолампа с вольфрамовым катодом прямого накала. Нагрев катода осуществляется постоянным током. Амперметр и вольтметр в цепи накала служат для определения мощности, расходуемой на нагрев катода, что необходимо для определения температуры.
Электрическая схема для проведения опыта представлена на рис. 13.4 и 13.5. В качестве диода в работе используется радиолампа с вольфрамовым катодом прямого накала. Нагрев катода осуществляется постоянным током. Амперметр и вольтметр в цепи накала служат для определения мощности, расходуемой на нагрев катода, что необходимо для определения температуры. , а также мощность, приходящуюся на единицу площади катода:
, а также мощность, приходящуюся на единицу площади катода: 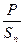 . Для данной лампы площадь поверхности катода принять Sn=3.52×10-2 см2.
. Для данной лампы площадь поверхности катода принять Sn=3.52×10-2 см2. , принять S=11×10-6 м2.
, принять S=11×10-6 м2. от (1/Т), откладывая по оси абсцисс х=(1/Т), а по оси ординат –
от (1/Т), откладывая по оси абсцисс х=(1/Т), а по оси ординат –  (рис.13.3).
(рис.13.3). и рассчитать работу выхода по формуле (13.10). Все данные занести в табл.13.3.
и рассчитать работу выхода по формуле (13.10). Все данные занести в табл.13.3.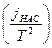

 , К-1
, К-1
 , Дж
, Дж


 . (14.1)
. (14.1) . (14.2)
. (14.2) . (14.3)
. (14.3) ) возвращающую силу, действующую на атом:
) возвращающую силу, действующую на атом: . (14.4)
. (14.4) (это сила, действующая на атом в состоянии равновесия) должно быть равно нулю, иначе атомы в среднем обладали бы ускорением и сместились из положения равновесия. Так что:
(это сила, действующая на атом в состоянии равновесия) должно быть равно нулю, иначе атомы в среднем обладали бы ускорением и сместились из положения равновесия. Так что: . (14.5)
. (14.5) , и что в гармоническом приближении (g=0) из (14.5) следует
, и что в гармоническом приближении (g=0) из (14.5) следует  , и теплового расширения нет. Этот результат не зависит от амплитуды колебаний атомов. Атомы колеблются гармонически, и в среднем их позиции в кристаллической решётке не зависят от температуры.
, и теплового расширения нет. Этот результат не зависит от амплитуды колебаний атомов. Атомы колеблются гармонически, и в среднем их позиции в кристаллической решётке не зависят от температуры. . (14.6)
. (14.6) можно при высоких температурах воспользоваться классическим законом распределения энергии по степеням свободы:
можно при высоких температурах воспользоваться классическим законом распределения энергии по степеням свободы: , (14.7)
, (14.7) , так что отклонения атомов от положения равновесия
, так что отклонения атомов от положения равновесия  становятся зависящими от температуры, а тепловая деформация
становятся зависящими от температуры, а тепловая деформация , (14.8)
, (14.8) . (14.9)
. (14.9)