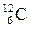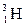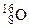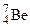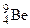|
|
В нерелятивистском случае
где m0 – масса покоя частицы. В релятивистском случае
где Е0 = m0с2 – энергия покоя частицы. Формула (1) с учетом соотношений (2) и (3) запишется: в нерелятивистском случае
в релятивистском случае
Сравним кинетические энергии электрона, прошедшего заданные в условии задачи разности потенциалов U1 = 51 В и U2 = 510 кВ, с энергией покоя электрона и в зависимости от этого решим, которую из формул (4) или (5) следует применить для вычисления длины волны де Бройля. Как известно, кинетическая энергия электрона Т, прошедшего ускоряющую разность потенциалов U, Т=eU. В первом случае Т1 = eU1 = 51 эВ = 0, 51×10-4 МэВ, что много меньше энергии покоя электрона Е0 = m0с2 = 0, 51 МэВ. Следовательно, в этом случае можно применить формулу (4). Для упрощения расчетов заметим, что Т1= 10-4 m0с2. Подставив это выражение в формулу (4), перепишем ее в виде Учитывая, что Во втором случае кинетическая энергия Т2 = eU2 = 510 кэВ = 0, 51 МэВ, т.е. равна энергии покоя электрона. В этом случае необходимо применить релятивистскую формулу (5). Учитывая, что Т2 = 0, 51 МэВ = m0с2, по формуле (5) найдем
№ 3. Кинетическая энергия электрона в атоме водорода составляет величину порядка T = 10 эВ. Используя соотношение неопределенностей, оценить минимальные линейные размеры атома. Р е ш е н и е. Соотношение неопределенностей для координаты и импульса имеет вид Из соотношения неопределенностей следует, что чем точнее определяется положение частицы в пространстве, тем более неопределенным становится импульс, а, следовательно, и энергия частицы. Пусть атом имеет линейные размеры l, тогда электрон атома будет находиться где –то в пределах области с неопределенностью Δх = l/2 . (1) Соотношение неопределенностей (1) можно записать в этом случае в виде
Физически разумная неопределенность импульса Dр во всяком случае не должна превышать значения самого импульса р, т.е. Dр » р. Импульс р связан с кинетической энергией Т соотношением Подставим числовые значения и произведем вычисления:
№ 4. Вычислить дефект массы и энергию связи ядра Р е ш е н и е. Масса ядра всегда меньше суммы масс свободных (находящихся вне ядра) протонов и нейтронов, из которых ядро образовалось. Дефект массы ядра Dm и есть разность между суммой масс свободных нуклонов (протонов и нейтронов) и массой ядра, т.е.
где Z – атомный номер (число протонов в ядре); А – массовое число (число нуклонов в ядре); mр, mn, m – соответственно, массы протона, нейтрона и ядра. В справочных таблицах всегда даются массы нейтральных атомов, но не ядер, поэтому формулу (1) целесообразно преобразовать так, чтобы в нее входила масса М нейтрального атома. Можно считать, что масса нейтрального атома равна сумме масс ядра и электронов, составляющих нейтральную оболочку атома: М = m+Zme , откуда m = М - Zme. Выразив в равенстве (1) массу ядра по последней формуле, получим Δm = Ζmp+ (A – Ζ)mn – M +Ζme, или Δm = Ζ(mp +me) + (A – Ζ)mn – M. Замечая, что mе + mp= MH, где MH – масса атома водорода, окончательно получим
Подставив в выражение (2) числовые значения масс (из справочных таблиц), получим
Энергией связи DЕ ядра называется энергия, которая в той или иной форме выделяется при образовании ядра из свободных нуклонов. В соответствии с соотношением пропорциональности массы и энергии Е = с2Dm, (3) или с2= Е /Dm = 9×1016Дж/кг. Если вычислить энергию связи, пользуясь внесистемными единицами, то с2 = 931 МэВ/а.е.м. С учетом этого формула (3) примет вид Е = 931 Dm (МэВ). (4) Подставив ранее найденное значение дефекта массы ядра в формулу (4), получим Е = 931×0,04216МэВ = 39,2 МэВ.
№ 5. При соударении a – частицы с ядром бора Р е ш е н и е. Обозначим неизвестное ядро символом Применив закон сохранения числа нуклонов, получим уравнение 4 +10 = 1 + А, откуда А = 13. Применив закон сохранения заряда, получим уравнение 2 + 5 = 1 +Z, откуда Z = 6. Следовательно, неизвестное ядро является ядром изотопа атома углерода Энергетический эффект Q ядерной реакции определяется по формуле Q = 931 [(mHe+ mB) – ( mH + mC)]. Здесь в первых круглых скобках указаны массы исходных ядер, во вторых скобках – массы ядер – продуктов реакции. При числовых подсчетах по этой формуле массы ядер заменяют массами нейтральных атомов. Возможность такой замены вытекает из следующих соображений. Число электронов в электронной оболочке нейтрального атома равно его зарядовому числу Z. Сумма зарядовых чисел исходных ядер равна сумме зарядовых чисел ядер – продуктов реакции. Следовательно, электронные оболочки ядер гелия и бора содержат вместе столько же электронов, сколько их содержат электронные оболочки ядер углерода и водорода. Очевидно, что при вычитании суммы масс нейтральных атомов углерода и водорода из суммы масс атомов гелия и бора массы электронов выпадут, и мы получим тот же результат, как если бы брали массы ядер. Подставив массы атомов, взятые из справочной таблицы в расчетную формулу, получим Q = 931 [(4,00260+10,01294)-(1,00783+13,00335)]Мэв = 4,06 МэВ.
№ 6. Определить начальную активность радиоактивного препарата магния 27Mg массой m = 0,2 мкг, а также его активность А через время t = 6 ч. Период полураспада T1/2 магния считать известным. Р е ш е н и е. Активность А изотопа характеризует скорость радиоактивного распада и равняется числу ядер, распадающихся в единицу времени: Согласно основному закону радиоактивного распада Очевидно, что начальная активность при t = 0 А0 = lN0. (1) Поэтому закон изменения активности со временем выражается формулой
Начальную активность определим по формуле (1). Входящая в эту формулу постоянная радиоактивного распада l может быть выражена через период полураспада соотношением l = ln2/T1/2 = 0,693/T1/2. Для 27Mgпериод полураспада T1/2 = 10 мин = 600 с. Следовательно, l = 0,693/600с-1 = 1,15×10-3 с-1. Число радиоактивных атомов N0, содержащихся в изотопе, равно произведению числа Авогадро NA на количество вещества n данного изотопа: Вычислим по формуле (1) начальную активность изотопа: А0 = lN0 = 1,15×10-3×4,46×1015 Бк = 5,13×1012 Бк. Или А0 = 5,13 ТБк. Активность через 6 ч (6ч = 2,16×104 с) получим по формуле (2):
№ 7. Космическое излучение на уровне моря на экваторе образует в воздухе объемом V = 1 см3 в среднем N = 24 пары ионов за время t1 = 10 c. Определить экспозиционную дозу X, получаемую человеком за время t2 = 1 год. Р е ш е н и е. Экспозиционную дозу, получаемую человеком, можно выразить формулой
где X – мощность экспозиционной дозы излучения. Мощность дозы Формула (1) с учетом выражений для
ТРЕНИРОВОЧНЫЕ ЗАДАЧИ
1. Определить энергию ε фотона, испускаемого при переходе электрона в атоме водорода с третьего энергетического уровня на основной. (Ответ. 12,1 эВ). 2. Определить первый потенциал возбуждения φ атома водорода. (Ответ. 10,2 В). 3. Вычислить длину волны де Бройля λ для электрона, прошедшего ускоряющую разность потенциалов U = 22,6 В.(Ответ. 0,258 нм). 4. Вычислить длину волны де Бройля λ для протона, движущегося со скоростью v = 0,6 с (с – скорость света в вакууме). (Ответ. 1,76 нм). 5. Оценить с помощью соотношения неопределенностей минимальную кинетическую энергию Tmin электрона, движущегося внутри сферической области диаметром d = 0,1 нм. (Ответ.15 эВ). 6. Если допустить, что неопределенность координаты движущейся частицы равна дебройлевской длине волны, то какова будет относительная неопределенность Δр/р импульса этой частицы? (Ответ. 0,16). 7. Вычислить энергию связи Есв ядра дейтерия (Ответ. 2,22 МэВ; 8,47 МэВ). 8. Вычислить энергетический эффект Q реакции (Ответ. 5,71 МэВ). 9. То же для реакции 10. Определить число N атомов радиоактивного препарата йода 11. Определить активность А радиоактивного препарата 12. При делении ядра урана 235U под действием замедленного нейтрона образовались осколки с массовыми числами М1 = 90 и М2 = 143. Определить число нейтронов, вылетевших из ядра в данном акте деления. Определить энергию и скорость каждого из осколков, если они разлетаются в противоположные стороны и их суммарная кинетическая энергия Т равна 160 МэВ. (Ответ. 98,2 МэВ; 61,8 МэВ;) 1,45×107 м/с; 0,91× 107 м/с.). 13. Воздух в некотором объеме V облучается рентгеновскими лучами. Доза излучения 4,5 Р. Найти, какая доля атомов, находящихся в данном объеме, будет ионизована этим излучением. (Ответ. 3,5×10-10). 14. Вычислить толщину слоя половинного ослабления Х1/2 параллельного пучка γ – излучения для воды, если линейный коэффициент ослабления μ = 0,047 см-1. (Ответ.14,7 см). 15. Воздух, находящийся при нормальных условиях в ионизационной камере объемом 6 см3, облучается рентгеновскими лучами. Мощность дозы рентгеновских лучей 0,48 мР/час. Найти ионизационный ток насыщения. (Ответ. 2,7×10-16А). 16. Так как свинец является конечным продуктом распада уранового ряда, то из отношения массы урана в руде к массе свинца, содержащегося в урановой руде, можно определить возраст руды. Определить возраст урановой руды, если известно, что на 1 кг урана
4.3. КОНТРОЛЬНАЯ РАБОТА № 6
600. Определить наибольшую и наименьшую длины волн в первой инфракрасной серии водорода (Серия Пашена). 601. Найти радиус первой боровской орбиты электрона в атоме водорода. 602. Определить максимальную энергию фотона серии Бальмера в спектре излучения атомарного водорода. 603. Двухзарядный ион лития Li++ перешел со второго энергетического уровня на первый. Определить длину волны, испускаемую при этом переходе. 604. Найти энергию и потенциал ионизации ионов лития Li++. 605. Какова кинетическая энергия электрона в атоме водорода на первойборовской орбите? 606. Найти период обращения на первой боровской орбите. 607. Найти скорость электрона на первой боровской орбите. 608. Определить энергию фотона, испускаемого атомом водорода при переходе электрона со второй орбиты на первую. 609. Определить длину волны, соответствующую третьей линии серии Бальмера. 610. Электрон движется по окружности радиусом 0,5 см в однородном магнитном поле с индукцией 8 мТл. Определить длину волны де Бройля электрона. 611. Кинетическая энергия электрона равна 1 кэВ. Найти длину волны де Бройля электрона. 612. С какой скоростью движется электрон, если дебройлевская длина волны численно равна его комптоновской длине волны. 613. Найти длину волны де Бройля для протона, прошедшего ускоряющую разность потенциалов в 1 кВ и 1 MB. 614. Кинетическая энергия электрона равна удвоенному значению его энергиипокоя.Вычислить длину волны де Бройля для такого электрона. 615. Длина волны де Бройля электрона равна 0,5 616. Вычислить длину волны де Бройля для электрона, движущегося покруговойорбите атома водорода, находящегося в основном состоянии. 617. Протон прошел ускоряющую разность потенциалов 10 В. Вычислить длину волны де Бройля протона. 618. Вычислить длину дебройлевской волны электрона, находящегося на второй орбите в атоме водорода. 619. Электрон летит со скоростью, равной 0,8 скорости света. Вычислить длину волны де Бройля электрона. 620. За один год начальное количество радиоактивного нуклида уменьшилось в 3 раза. Во сколько раз оно уменьшится за 2 года? 621. Определить активность 1 мг фосфора 622. Сколько процентов начального количества актиния 623. Из каждого миллиона атомов радиоактивного изотопа каждую секунду распадается 200 атомов. Определить период полураспада Т1/2 изотопа. 624. Какая доля начального количества атомов распадается за один год в радиоактивном изотопе тория 625. Вычислить удельную активность 626. Определить постоянные распада изотопов радия: 627. Вычислить число атомов радона, распавшихся в течение первых суток, если первоначальная масса радона была 1 г. 628. Какова вероятность того, что данный атом в образце радиоактивного йода 629. За сутки активность нуклида уменьшилась от 3,2 Бк до 0,2 Бк. Определить период полураспада этого нуклида. 630. Во сколько раз отличается удельная энергия связи (энергия связи, рассчитанная на один нуклон) для ядер 631. Определить дефект массы и энергию связи ядра, состоящего из трех протонов и четырех нейтронов. 632. Определить удельную энергию связи (т.е. среднюю энергию связи, рассчитанную на один нуклон) ядра 633. Какое количество энергии освободится при соединении одного протона и двух нейтронов в атомное ядро? 634. Определить дефект массы и энергию связи ядра атома тяжелого водорода. 635. Какую наименьшую энергию нужно затратить, чтобы разделить на отдельные нуклоны ядро 636. Масса α - частицы (ядро гелия 637. Во сколько раз отличается удельная энергия связи (энергия связи, рассчитанная на один нуклон) для ядер 638. Вычислить удельную энергию связи ядра 639. Какую наименьшую энергию нужно затратить, чтобы оторвать один нейтрон от ядра 640. Вычислить энергию ядерной реакции в МэВ:
641. Вычислить энергию ядерной реакции в МэВ:
642. Вычислить энергию ядерной реакции в МэВ:
643. Вычислить энергию ядерной реакции в МэВ: 644. Вычислить энергию ядерной реакции в МэВ:
645. Вычислить энергию ядерной реакции в МэВ:
646. Вычислить энергию ядерной реакции в МэВ:
647. Вычислить энергию ядерной реакции в МэВ:
648. Вычислить энергию ядерной реакции в МэВ:
649. Вычислить энергию ядерной реакции в МэВ:
650. Какой порядковый номер в таблице Менделеева имеет элемент, который образуется в результате излучения γ – кванта ядром элемента с порядковым номером Z? 651. При бомбардировке изотопа азота 652. Написать недостающее обозначение в ядерной реакции: Х + 653. Определить число протонов и число нейтронов в ядре изотопа урана 654. Написать недостающее обозначение в ядерной реакции: 655. Какой заряд будет иметь атомное ядро изотопа урана 656. Написать недостающее обозначение в ядерной реакции:
657. Какое массовое число будет иметь атомное ядро изотопа урана
658. При бомбардировке изотопа 659. Какая частица испускается в результате бомбардировки ядер азота ВОПРОСЫ ДЛЯ ПОДГОТОВКИ К ЭКЗАМЕНУ
1. Свет как электромагнитная волна (ЭМВ). Поперечный характер ЭМВ. Уравнение ЭМВ. Волновое уравнение. Длина волны. Скорость распространения света. 2. Закон преломления ЭМВ на границе раздела сред. Показатель преломления. Принцип Ферма. Геометрические и оптические длина пути и разность хода. 3. Интерференция света. Условия получения интерференционной картины. Условия максимума и минимума при интерференции. 4. Когерентность. Получение когерентных волн (классические интерференционные опыты). Опыт Юнга. Расчет интерференционной картины от двух источников. 5. Интерференция в тонких пленках. Линии равного наклона и линии равной толщины. 6. Кольца Ньютона. Просветленная оптика. Интерферометры, рефрактометры. 7. Дифракция света. Принцип Гюйгенса-Френеля. Метод зон Френеля. 8. Дифракция Френеля на простейших преградах (диафрагма, диск). Зонные пластинки. 9. Дифракция Фраунгофера. Дифракция Фраунгофера на одной и двух щелях. 10. Дифракция Фраунгофера на дифракционной решетке (ДР). Дисперсия и разрешающая способность ДР. Применение ДР. 11. Поляризация света. Виды поляризованного света. Закон Малюса. 12. Поляризация света при отражении и преломлении. Закон Брюстера. 13. Двойное лучепреломление. Поляризующие устройства (призма Николя и др.). Поляризаторы. 14. «Интерференция» поляризованного света. Искусственная анизотропия. 15. Плоскость поляризации. Вращение плоскости поляризации. Поляриметры. 16. Тепловое излучение, его характеристики. Абсолютно черное тело. 17. Распределение энергии в спектре излучения абсолютно черного тела. Законы Кирхгофа, Стефана-Больцмана, Вина. 18. Распределение энергии в спектре излучения абсолютно черного тела. Гипотеза и формула Планка. 19. Фотоэффект. Законы фотоэффекта. Уравнение Эйнштейна. 20. Энергия и импульс фотона. Эффект Комптона. Световое давление. 21. Развитие представлений о строении атома. Модели Томсона и Резерфорда. Спектры излучения и поглощения в атомах водорода. Опыты Франка и Герца. 22. Постулаты Бора. Квантование орбит. Боровская теория атома водорода. 23. Волновые свойства вещества. Гипотеза де Бройля. Принцип неопределенностей. 24. Понятие о квантовой (волновой) механике. Волновая функция, ее физический смысл. Уравнение Шредингера. 25. Квантовомеханическое описание состояния электрона в атоме. Заполнение электронных оболочек. Принцип Паули. Периодическая система элементов. 26. Спонтанное и вынужденное излучение света. Инверсия заселенностей энергетических уровней. Принцип работы лазера. 27. Основы зонной теории твердых тел. Металлы, полупроводники, изоляторы. Основы квантовой статистики. 28. Полупроводники. Собственная и примесная проводимости полупроводников. 29. Полупроводниковые диоды и триоды. 30. Характеристики атомного ядра. Атомная единица массы. Изотопы. Открытие нейтрона. Состав атомного ядра. 31. Устойчивость атомных ядер. Энергия связи. Деление тяжелых ядер и синтез легких. Термоядерная энергия. 32. Радиоактивность. Закон радиоактивного распада. 33. Современная физическая картина мира: вещество и поле. Атомно-молекулярное строение вещества. Элементарные частицы: лептоны, адроны. Кварки. Взаимопревращение частиц. Гравитационное, электромагнитное, слабое и сильное ядерные взаимодействия. Единая теория поля. Элементы космологии.
6. CПРАВОЧНЫЕ ТАБЛИЦЫ
6.1. Показатель преломления
6.2. Работа выхода электронов
6.3. Масса и энергия покоя некоторых частиц
6.4. Периоды полураспада радиоактивных изотопов
6.5. Массы изотопов, а.е.м.
h = 6,63×10-34 Дж∙с; R = 2,07×10-18 с-1; с = 3×108 м/с; | е | = 1,6×10-19 Кл; 1 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , (2)
, (2) , (3)
, (3) , (4)
, (4)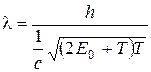 . (5)
. (5) .
. есть комптоновская длина волны l, получим
есть комптоновская длина волны l, получим  . Так как l = 2, 43 пм, то
. Так как l = 2, 43 пм, то  .
. , или
, или  .
. , где Dx – неопределенность координаты частицы (в данном случае электрона); Dр – неопределенность импульса частицы (электрона);
, где Dx – неопределенность координаты частицы (в данном случае электрона); Dр – неопределенность импульса частицы (электрона);  – постоянная Планка, деленная на 2p.
– постоянная Планка, деленная на 2p.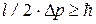 , откуда
, откуда . (2)
. (2) . Заменим Dр на
. Заменим Dр на  (такая замена не увеличит l). Переходя от неравенства к равенству, получим
(такая замена не увеличит l). Переходя от неравенства к равенству, получим  .
. .
. .
. , (1)
, (1) . (2)
. (2)
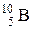 произошла ядерная реакция, в результате которой образовалось два новых ядра. Одно из них – ядро атома водорода
произошла ядерная реакция, в результате которой образовалось два новых ядра. Одно из них – ядро атома водорода  . Определить порядковый номер и массовое число второго ядра, дать символическую запись ядерной реакции и определить ее энергетический эффект.
. Определить порядковый номер и массовое число второго ядра, дать символическую запись ядерной реакции и определить ее энергетический эффект. . Так как a – частица представляет собой ядро гелия
. Так как a – частица представляет собой ядро гелия  , запись реакции имеет вид
, запись реакции имеет вид 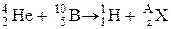 .
. .
. , где dN – число ядер, распавшихся за время dt.
, где dN – число ядер, распавшихся за время dt. , где l – постоянная радиоактивного распада. Так как
, где l – постоянная радиоактивного распада. Так как  , где N0 – число не распавшихся ядер в момент времени, принятый за начальный, то
, где N0 – число не распавшихся ядер в момент времени, принятый за начальный, то  .
.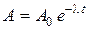 . (2)
. (2) , где m – масса изотопа; m – молярная масса. Выразив в этой формуле значения величин в системе Си, получим
, где m – масса изотопа; m – молярная масса. Выразив в этой формуле значения величин в системе Си, получим  ядер = 4,46×1015 ядер.
ядер = 4,46×1015 ядер. .
.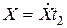 , (1)
, (1) , где Q – заряд ионов одного знака, образуемых излучением за время t1 в воздухе массой m. Масса m = rV. Заряд всех ионов одного знака найдем, умножив элементарный заряд на число ионов: Q =êeêN.
, где Q – заряд ионов одного знака, образуемых излучением за время t1 в воздухе массой m. Масса m = rV. Заряд всех ионов одного знака найдем, умножив элементарный заряд на число ионов: Q =êeêN. и Q примет вид
и Q примет вид  . Выразим величины, входящие в формулу (2), в единицах СИ и, выполнив вычисления, получим: X = 9,41 мкКл/кг.
. Выразим величины, входящие в формулу (2), в единицах СИ и, выполнив вычисления, получим: X = 9,41 мкКл/кг. и трития
и трития  .
.
 (Ответ. 4,03 МэВ).
(Ответ. 4,03 МэВ).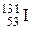 массой m = 0,5 мкг, распавшихся в течение времени: 1) t1 = 1 мин; 2) t2 = 7 сут. (Ответ. 1,38×1011; 1,04×1015).
массой m = 0,5 мкг, распавшихся в течение времени: 1) t1 = 1 мин; 2) t2 = 7 сут. (Ответ. 1,38×1011; 1,04×1015). массой m = 1мкг. (Ответ. 543 кБк).
массой m = 1мкг. (Ответ. 543 кБк). в этой руде приходится 320 г свинца
в этой руде приходится 320 г свинца 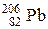 . (Ответ. 3×109 лет).
. (Ответ. 3×109 лет).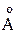 . Какую ускоряющую разность потенциалов прошел электрон?
. Какую ускоряющую разность потенциалов прошел электрон? .
. останется через 5 дней.
останется через 5 дней. ?
? .
. .
. распадается в течение ближайшей секунды?
распадается в течение ближайшей секунды? ?
? .
. ?
? Не) равна 4,00150 а.е.м. Определить массу нейтрального атома гелия.
Не) равна 4,00150 а.е.м. Определить массу нейтрального атома гелия. Li и
Li и  Ве ?
Ве ? О.
О. N?
N? Be +
Be +  +
+  n.
n. B +
B +  n →
n →  Li +
Li +  He.
He.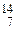 N +
N +  n →
n →  H +
H +  C.
C. А1+
А1+  Si +
Si +  Н.
Н. H +
H +  H →
H →  He +
He +  Не +
Не +  Hе.
Hе. H →
H →  .
. O.
O. Н +
Н +  +
+  Na +
Na +  U.
U. Mn + X →
Mn + X →  Fe +
Fe +  U после α - распада и двух β - распадов.
U после α - распада и двух β - распадов. F +
F +  P, который затем распадается с выделением позитронов. Написать уравнения этих реакций.
P, который затем распадается с выделением позитронов. Написать уравнения этих реакций.