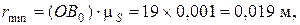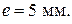|
|
С поступательно движущимся толкателемПостроение диаграмм движения толкателя (коромысла)
Вычерчиваем диаграмму аналога ускорения толкателя
где
Подставляя численные значения, получим
Для построения диаграммы перемещения выходного звена по углу поворота кулачка необходимо выполнить двукратное интегрирование второй производной от перемещения выходного звена по углу поворота кулачка. В соответствии с заданием в интервале угла удаления Для построения диаграммы аналога скорости Через точки 1, 2, 3, …, 13 проводим ординаты, которые делят всю площадь заданных диаграмм на ряд участков. Площадь каждого из участков заменяем равновеликим прямоугольником с общим основанием по оси абсцисс. Проектируем высоты полученных треугольников на ось ординат. Точки проекций 1', 2', 3', …, 13' соединяем с полюсом Р2, взятым на произвольном полюсном расстоянии Н2 от начала осей координат О, лучами Р21', Р22', Р23', …, Р213'. Ось абсцисс диаграммы Диаграмма аналогов скоростей на участке, соответствующем углу Диаграмму перемещения толкателя Вычислим масштабные коэффициенты диаграмм. Масштаб по оси абсцисс диаграмм
Подставив численные значения, получим
Масштабный коэффициент по оси ординат диаграммы перемещений
где h — максимальное перемещение толкателя (центра ролика), мм; Smax — максимальная ордината диаграммы перемещений, мм.
В интервале угла удаления
В интервале угла возвращения
Масштабный коэффициент по оси ординат диаграммы
В интервале угла удаления
В интервале угла возвращения
Масштабный коэффициент по оси ординат диаграммы
В интервале угла удаления
В интервале угла возвращения
Разметку траектории точки В (центра ролика) производим в соответствии с диаграммой Аналогично осуществляем разметку траектории точки В толкателя в интервале угла возвращения.
Построение профиля кулачка с поступательно движущимся толкателем
4.2.1 Определение минимал с поступательно движущимся толкателем
Для кулачковых механизмов минимальный радиус и другие основные размеры определяются по допускаемому углу давления или минимальному углу передачи движения путем графического определения области возможного расположения центра вращения кулачка. Для определения минимального радиуса кулачка rmin и величины эксцентриситета е строим диаграмму По диаграмме
где
и фазы возвращения:
где
Для примера определим значения
Для остальных положений расчеты проводим аналогично и результаты сводим в таблицу 4.1.
Таблица 4.1 — Результаты расчета аналогов скоростей
Откладываем эти значения на параллельных прямых в масштабе Определим минимальный радиус кулачка и эксцентриситет:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , для чего на оси абсцисс в произвольном масштабе
, для чего на оси абсцисс в произвольном масштабе  откладываем заданные углы
откладываем заданные углы  ,
,  ,
,  (приложение О). Для принятой длины диаграммы
(приложение О). Для принятой длины диаграммы 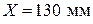 величины отрезков, изображающих фазовые углы:
величины отрезков, изображающих фазовые углы: (4.1)
(4.1)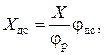 (4.2)
(4.2) (4.3)
(4.3) — рабочий угол кулачка, град.
— рабочий угол кулачка, град.
 (4.4)
(4.4)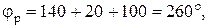
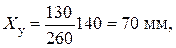
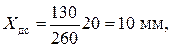
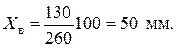
 в произвольном масштабе строим закон равномерно убывающего ускорения, а в интервале угла возвращения
в произвольном масштабе строим закон равномерно убывающего ускорения, а в интервале угла возвращения  – косинусоидальный. Для построения косинусоиды в правой части диаграммы строим вспомогательную полуокружность, которую делим на шесть равных частей (приложение Г).
– косинусоидальный. Для построения косинусоиды в правой части диаграммы строим вспомогательную полуокружность, которую делим на шесть равных частей (приложение Г).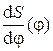 интегрируем построенную диаграмму
интегрируем построенную диаграмму  лельно лучу Р22' проводим линию до пересечения с ординатой 2 и т.д. Полученная ломаная и представляет приближенно искомую интегральную кривую
лельно лучу Р22' проводим линию до пересечения с ординатой 2 и т.д. Полученная ломаная и представляет приближенно искомую интегральную кривую 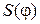 строим методом графического интегрирования кривой
строим методом графического интегрирования кривой  (4.5)
(4.5)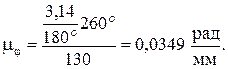
 (4.6)
(4.6)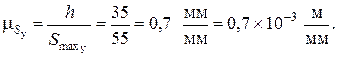
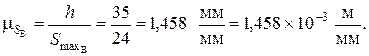
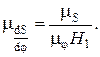 (4.7)
(4.7)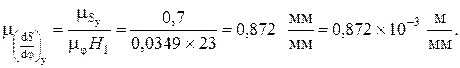

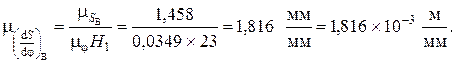
 (4.7)
(4.7)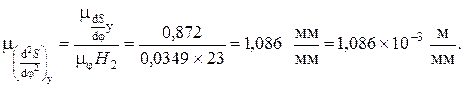
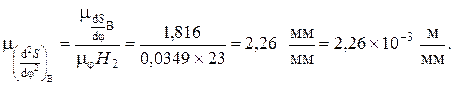
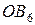 , равный максимальному перемещению толкателя. Конечную точку
, равный максимальному перемещению толкателя. Конечную точку  соединяем с конечной точкой 6' проекции наибольшей ординаты 6 — 6. Через точки 1', 2', …, 5' проводим прямые, параллельные 6' — В6. Полученные точки В1, В2, …, В6 дают разметку траектории толкателя в интервале угла удаления.
соединяем с конечной точкой 6' проекции наибольшей ординаты 6 — 6. Через точки 1', 2', …, 5' проводим прямые, параллельные 6' — В6. Полученные точки В1, В2, …, В6 дают разметку траектории толкателя в интервале угла удаления. ьного радиуса кулачка rmin
ьного радиуса кулачка rmin . Для этого проводим оси координат S и
. Для этого проводим оси координат S и  . По оси ординат S в масштабе
. По оси ординат S в масштабе  отложим перемещения толкателя, взятые из разметки хода толкателя на диаграмме перемещений. Через полученные точки В0, В1, В2, … проводим прямые, параллельные оси абсцисс.
отложим перемещения толкателя, взятые из разметки хода толкателя на диаграмме перемещений. Через полученные точки В0, В1, В2, … проводим прямые, параллельные оси абсцисс. (4.8)
(4.8) — длина ординаты в i-том положении на диаграмме аналогов скоростей для фазы удаления, мм;
— длина ординаты в i-том положении на диаграмме аналогов скоростей для фазы удаления, мм;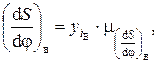 (4.8а)
(4.8а) — длина ординаты в i-том положении на диаграмме аналогов скоростей для фазы возвращения, мм.
— длина ординаты в i-том положении на диаграмме аналогов скоростей для фазы возвращения, мм.

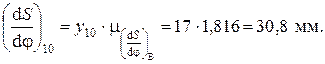
 Причем для фазы удаления эти отрезки откладываются в сторону вращения кулачка, а для возвращения — в обратную. Соединив плавной кривой концы отложенных отрезков, построим кривую
Причем для фазы удаления эти отрезки откладываются в сторону вращения кулачка, а для возвращения — в обратную. Соединив плавной кривой концы отложенных отрезков, построим кривую  (см. задание) к оси
(см. задание) к оси