
|
|
Задачи для работы в аудиторииПрактическое занятие 6 ДИНАМИКА
Примеры решения задач
Решение. Тело можно принять за материальную точку, которая движется по окружности в горизонтальной плоскости с постоянной линейной скоростью. Из этого следует, что тангенциальное ускорение
где Покажем на рис. 2.7 все силы, действующие на груз: силу тяжести Второй закон Ньютона (или уравнение движения) в векторной форме имеет вид
Выберем систему отсчета, как показано на рис. 2.7. Перепишем второй закон Ньютона в скалярном виде в проекциях на оси координат: на ось
на ось
Решая эти уравнения относительно силы натяжения нити
Полное ускорение груза
Поскольку
Задача 2.9. Чтобы двигаться по окружности радиусом R со скоростью v, велосипедист, повернув руль, должен наклониться в сторону поворота. Найти угол наклона велосипедиста к плоскости дороги.
Систему координат выберем так, чтобы ось ОХ была направлена к центру окружности, а ось ОY – вертикально вверх. В проекциях на эти оси составим уравнения на основании второго закона Ньютона:
или
Разделив почленно последнее уравнение на предпоследнее, получим
2.17. Ведро с водой вращают в вертикальной плоскости на веревке длиной – Не знаю, с чего начинать – п. 92. – Не понимаю, как учесть условие, что вода остается в ведре – п. 102. – Не знаю, как найти ускорение – п. 132.
Задачи для работы в аудитории
2.62. На каком расстоянии от поверхности Земли ускорение свободного падения равно 1 м/с2? 2.63. Какие силы действуют на спутник, движущийся вокруг Земли? Падает ли спутник на Землю? 2.64. Почему на экваторе Земли тело весит меньше, чем на полюсе? 2.65. Какой продолжительности должны быть сутки на Земле, чтобы тела на экваторе были невесомы? 2.69. Тело массой т находится на горизонтальном диске на расстоянии r от оси. Диск начинает раскручиваться с малым ускорением. Построить график зависимости составляющей силы трения в радиальном направлении, действующей на тело, от угловой скорости вращения диска. При какой угловой скорости диска начнется соскальзывание тела? 2.79. Самолет делает «мертвую петлю» радиуса R = 500 м с постоянной скоростью u = 360 км/ч. Найти вес летчика массы т = 70 кг в нижней, верхней и средней точках петли.
Задачи для самостоятельного решения
2.66. Найти зависимость веса тела от географической широты. 2.67. Какова первая космическая скорость для планеты, масса и радиус которой в два раза больше, чем у Земли? 2.68. Человек сидит на краю круглой горизонтальной платформы радиусом R = 4 м. С какой частотой n должна вращаться платформа вокруг вертикальной оси, чтобы человек не мог удержаться на ней при коэффициенте трения k = 0,27? 2.70. Автомобиль массой М = 3·103 кг движется с постоянной скоростью v = 36 км/ч: а) по горизонтальному мосту; б) по выпуклому мосту; в) по вогнутому мосту. Радиус кривизны моста в последних двух случаях R = 60 м. С какой силой давит автомобиль на мост (в последних двух случаях) в тот момент, когда линия, соединяющая центр кривизны моста с автомобилем, составляет угол α = 10° с вертикалью? 2.72. С какой наибольшей скоростью может двигаться автомобиль на повороте с радиусом закругления R = 150 м, чтобы его не «занесло», если коэффициент трения скольжения шин о дорогу k = 0,42? 2.74. Поезд движется по закруглению радиусом R = 800 м со скоростью v = 72 км/ч. Определить, на сколько внешний рельс должен быть выше внутреннего, чтобы на колесах не возникало бокового усилия. Расстояние между рельсами по горизонтали принять равным d = 1,5 м. 2.78. Мотоциклист едет по горизонтальной дороге со скоростью 72 км/ч, делая поворот радиусом кривизны 100 м. На сколько при этом он должен наклониться, чтобы не упасть на повороте?
ОТВЕТЫ 2.17. 2.62.13 600 км. 2.63. 2.64. 2.65.1ч. 25 мин. 2.66. 2.67. 2.68.7,77 мин-1. 2.69.См. график. 2.70.а) 29 400 Н; б) 24 000 Н; в) 34 000 Н. 2.71.8,2º. 2.72.89 км/ч. 2.73.54 км/ч. 2.74.7,64 см. 2.75.47º. 2.76.17 м/с. 2.77.Вес автогонщика может увеличиться в 1,08 раза. 2.78.22º. 2.79.2,1 кН; 0,7 кН; 1,6 кН. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
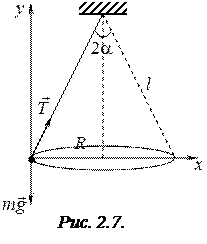 Задача 2.8. Груз массы
Задача 2.8. Груз массы  г, привязанный к нити длиной
г, привязанный к нити длиной 
 см, вращается в горизонтальной плоскости с постоянной скоростью так, что нить описывает коническую поверхность с углом при вершине
см, вращается в горизонтальной плоскости с постоянной скоростью так, что нить описывает коническую поверхность с углом при вершине  . Определить угловую скорость
. Определить угловую скорость  вращения груза и силу натяжения нити
вращения груза и силу натяжения нити  .
. , а полное ускорение определяется только нормальным, т.е.
, а полное ускорение определяется только нормальным, т.е. ,
,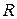 – радиус окружности, по которой движется груз.
– радиус окружности, по которой движется груз. и силу натяжения нити
и силу натяжения нити  , расположенные в плоскости рисунка (вертикальной плоскости).
, расположенные в плоскости рисунка (вертикальной плоскости).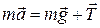 .
. :
: ,
, :
: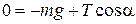 .
. Н.
Н. .
.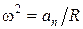 , где
, где  , окончательно для
, окончательно для 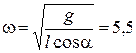 рад/с.
рад/с.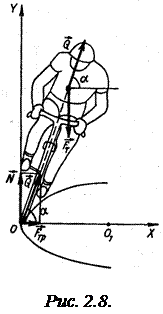 Решение. Когда велосипед наклонен, сила реакции дороги
Решение. Когда велосипед наклонен, сила реакции дороги  направлена под углом α к поверхности дороги (рис. 2.8). Эта сила является равнодействующей двух сил – силы нормальной реакции дороги
направлена под углом α к поверхности дороги (рис. 2.8). Эта сила является равнодействующей двух сил – силы нормальной реакции дороги 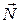 и силы трения покоя
и силы трения покоя  . Последняя всегда принимает такое значение, что сила
. Последняя всегда принимает такое значение, что сила  , направленная вертикально вниз.
, направленная вертикально вниз.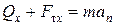 ,
, 
 ,
,  .
. . Следовательно, угол наклона велосипедиста
. Следовательно, угол наклона велосипедиста .
. м. С какой наименьшей скоростью надо его вращать, чтобы при прохождении верхней точки удержать воду в ведре?
м. С какой наименьшей скоростью надо его вращать, чтобы при прохождении верхней точки удержать воду в ведре?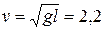 м/с.
м/с. 
 .
. 8 км/с.
8 км/с.