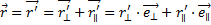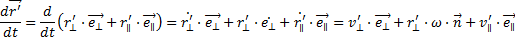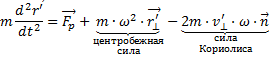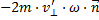Кинетическая энергия тела при плоскопараллельном движении.

При плоскопараллельном движении кинетиче­ская энергия тела равна энергии поступательного движения со скоростью центра масс, сло­женной скинетической энергией вращательного движения вокруг центра масс.

31) Гироскопический эффект. Угловая скорость процессии гироскопа.

Гироскопом называют быстро вращающееся тело, ось вращения которого может изменять свое направление в пространстве. Под действием внешних сил гироскоп может совершать движения, которые кажутся на первый взгляд неожиданными и противоречащими интуиции. На анимации изображён гироскоп в карданном подвесе, допускающем поворот оси массивного ротора вокруг трёх взаимно перпендикулярных осей, пересекающихся в его центре масс. На ось гироскопа подвешен маленький шарик. Если бы маховик гироскопа не вращался, то наблюдалось бы привычное явление: шарик опускался бы под действием собственного веса. Иначе происходит, когда маховик гироскопа приведен в быстрое вращение, как показано на анимации. В этом случае шарик опускаться не будет, а будет двигаться вместе с гироскопом по окружности в горизонтальной плоскости. Такое вращение называется вынужденной прецессией.

Движение гироскопа является следствием фундаментального уравнения механики (ниже все векторные величины обозначены жирным шрифтом, а скалярные величины - обычным шрифтом):

dL/dt = M

где L - вектор момента количества движения (или, иначе говоря, вектор момента импульса), t - время, М - вектор момента сил. В приближённой теории гироскопа пренебрегают моментом импульса, связанным с медленной прецессией гироскопа и считают, что момент импульса полностью определяется вращением маховика:

L = Iw

где I - момент инерции маховика гироскопа, w - вектор угловой частоты вращения маховика гироскопа. С другой стороны, момент сил М, действующих на гироскоп, равен

М = [a, F]

т.е. представляет собой векторное произведение радиус-вектора a, проведённого из центра гироскопа к точке приложения силы F=mg, где m - масса грузика, g - вектор ускорения свободного падения.

Момент количества движения L изменяется только вследствие прецессии гироскопа с угловой скоростью W. Поэтому

dL/dt = [W, L]

Окончательно получаем:

[W, Iw] = - [mg, a]

Так как вектор w сонаправлен вектору a , мы можем записать

W = - (am / Iw) g

Таким образом, мы можем видеть из этой формулы, что маховик гироскопа будет совершать медленное вращение (прецессию) в горизонтальной плоскости, причём угловая скорость прецессии тем больше, чем больше масса подвешенного грузика. Приведенные выше рассуждения справедливы при условии W<<w , т.е. для быстро вращающегося гироскопа. Для гироскопов, применяющихся в технике, величина угловой скорости прецессии бывает в миллионы раз меньше угловой скорости вращения маховика.

32.1. Неинерциальные системы отсчета.

Неинерциальные системы отчета.

Силы инерции.

Законы Ньютона выполняются только в инерциальных системах отсчета. Относительно всех инерциальных систем данное тело движется с одинаковым ускорением w. Любая неинерциальная система отсчета движется относительно инерциальных систем с некоторым ускорением, поэтому ускорение тела в неинерциальной системе отсчета w’ будет отлично от w. Обозначим разность ускорений тела в инерциальной и неинерциальной системах символом а:

w – w^, = a.

Для поступательно движущейся неинерциальной системы а одинаково для всех точек пространства (a=const) и представляет собой ускорение неинерциальной системы отсчета. Для вращающейся неинерциальной системы а в разных точках пространства будет различным (а=а(r’), где r’ — радиус-вектор, определяющий положение точки относительно неинерциальной системы отсчета).

33) Вращательные неинерциальные системы отсчета. Центробежная сила, сила Кориолиса и их свойства.

Вращательные неинерциальные системы отсчета – это такие системы отсчета, в которых все точки пространства в этой системе движутся с одинаковыми угловыми скоростями относительно инерциальной системы отсчета.

Свойства: Центробежная сила и сила Кориолиса – это фиктивные силы, то есть они связаны не с взаимодействием тел, а с выбором неинерциальной системы отсчета.

Центробежная сила
Сила Кориолиса

Центробежная сила — сила инерции, которую вводят во вращающейся (неинерциальной) системе отсчёта (чтобы применять законы Ньютона, рассчитанные только на инерциальные СО) и которая направлена от оси, вокруг которой происходит вращение тела — или — в двумерном случае — от центра вращения (отсюда и название).

Также центробежной силой, особенно в технической литературе, называют силу, действующую со стороны движущегося по круговой траектории тела на вызывающие это вращение связи, равная по модулю центростремительной силе и всегда направленная в противоположную ей сторону.

Сила Кориолиса — одна из сил инерции, существующая в неинерциальной системе отсчёта из-за вращения и законов инерции, проявляющаяся при движении в направлении под углом к оси вращения.

Не нашли, что искали? Воспользуйтесь поиском по сайту: