
|
|
Определение скоростей точек плоской фигурыБыло отмечено, что движение плоской фигуры можно рассматривать как слагающееся из поступательного движения, при котором все точки фигуры движутся со скоростью В самом деле, положение любой точки Мфигуры определяется по отношению к осям Охурадиусом-вектором
В полученном равенстве величина
Скорость
где Таким образом, скорость любой точки Мплоской фигуры геометрически складывается из скорости какой-нибудь другой точкиА, принятой за полюс, и скорости, которую точка Мполучает при вращении фигуры вокруг этого полюса. Модуль и направление скорости
Рис.30 Рис.31
23. Фактически уравнением поступательного движения твердого тела является уравнение второго закона Ньютона: Используя уравнения:
24.В этом случае составляющие
Вращение вокруг оси z происходит только под действием
6.4
или
Так как у всех точек разная, введем, вектор угловой скорости причем
Тогда
где R – расстояние от оси z до dm. Как видно, момент инерции I – величина скалярная.
получим или - Это основное уравнение динамики тела вращающегося вокруг неподвижной оси.
26) Момент импульса твердого тела.
Если ось вращения твердого тела закреплена, то момент силы перпендикулярный этой оси (
Скорость изменения момента импульса твердого тела вдоль оси вращения, которая закреплена, равняется результирующему моменту внешних сил, направленному вдоль этой оси.
28)Момент сил трения качения – закон Кулона. Коэффициент трения качения.
Трение качения. Существование трения качения можно установить экспериментально, например, при исследовании качения тяжелого цилиндра радиуса на горизонтальной плоскости.
Если цилиндр и плоскость - твердые тела с шероховатыми поверхностями (рис. 55, a), то их касание будет происходить в точке, сила N уравновешивает силу тяжести P, а горизонтальная сила Q и сила трения F образуют пару сил (Q,F) под действием которой цилиндр должен начинать движение при любых величинах силы Q. В действительности же цилиндр начинает движение после того, как величина силы Q превысит предельное значение Ql.
Этот факт можно объяснить, если предположить, что цилиндр и плоскость деформируются. Тогда их контакт будет происходить по малой площадке или лунке ( на рис. 55, b малая площадка изображена своим сечением). При увеличении силы Q центр давления будет перемещаться из середины сечения вправо. В результате образуется пара сил (P,N), которая препятствует началу движения цилиндра. В состоянии предельного равновесия на цилиндр действуют пара сил (Ql,F) с моментом Ql·r и уравновешивающая ее пара (P,N) с моментом N·δ, где δ - значение максимального смещения. Из равенства моментов пар сил находим (6)
Пока Q <Ql, цилиндр находится в покое, при Q >Ql начинается качение.
Обычно рис. 55, b упрощают, не изображая на нем смещения точки приложения нормальной реакции, добавляя к силам на рис. 55, a пару сил, препятствующую качению цилиндра, как показано на рис. 55, c.
Момент этой пары сил называется моментом трения качения, он равен моменту пары сил (P,N): (7)
Входящая в формулы (6) и (7) величина максимального смещения точки приложения нормальной реакции δ называется коэффициентом трения качения. Он имеет размерность длины и определяется экспериментально. Приведем приближенные значения этого коэффициента (в метрах) для некоторых материалов: дерево по дереву δ = 0,0005-0,0008; мягкая сталь по стали (колесо по рельсу) - 0.00005; закаленная сталь по стали (шарикоподшипник ) - 0.00001.
Отношение δ/r в формуле (6) для большинства материалов значительно меньше коэффициента трения покоя f0 . Поэтому в технике, когда это возможно, стремятся скольжение заменить качением (колеса, катки, шарикоподшипники и т.п.).
Закон Амонтона — Кулона Основная статья: Закон Кулона (механика) Не путать с законом Кулона! Основной характеристикой трения является коэффициент трения μ, который определяется материалами, из которых изготовлены поверхности взаимодействующих тел. В простейших случаях сила трения F и нормальная нагрузка (или сила нормальной реакции) Nnormal связаны неравенством обращающимся в равенство только при наличии относительного движения. Это соотношение называется законом Амонтона — Кулона. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 полюсаА, и из вращательного движения вокруг этого полюса. Покажем, что скорость любой точки М фигуры складывается геометрически из скоростей, которые точка получает в каждом из этих движений.
полюсаА, и из вращательного движения вокруг этого полюса. Покажем, что скорость любой точки М фигуры складывается геометрически из скоростей, которые точка получает в каждом из этих движений. (рис.30), где
(рис.30), где  - радиус-вектор полюсаА,
- радиус-вектор полюсаА,  - вектор, определяющий положение точки М относительно осей
- вектор, определяющий положение точки М относительно осей  , перемещающихся вместе с полюсом А поступательно (движение фигуры по отношению к этим осям представляет собой вращение вокруг полюса А). Тогда
, перемещающихся вместе с полюсом А поступательно (движение фигуры по отношению к этим осям представляет собой вращение вокруг полюса А). Тогда .
. есть скорость полюсаА; величина же
есть скорость полюсаА; величина же  равна скорости
равна скорости  , которую точка Мполучает при
, которую точка Мполучает при  , т.е. относительно осей
, т.е. относительно осей  , или, иначе говоря, при вращении фигуры вокруг полюса А. Таким образом, из предыдущего равенства действительно следует, что
, или, иначе говоря, при вращении фигуры вокруг полюса А. Таким образом, из предыдущего равенства действительно следует, что .
.
 ,
, - угловая скорость фигуры.
- угловая скорость фигуры. находятся построением соответствующего параллелограмма (рис.31).
находятся построением соответствующего параллелограмма (рис.31).

 и
и  получаем
получаем  – момента внешних сил, направленные вдоль x и y, компенсируются моментами сил реакции закрепления.
– момента внешних сил, направленные вдоль x и y, компенсируются моментами сил реакции закрепления.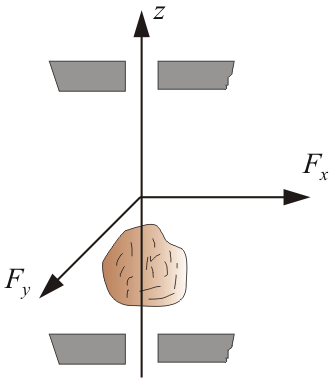 6.5
6.5 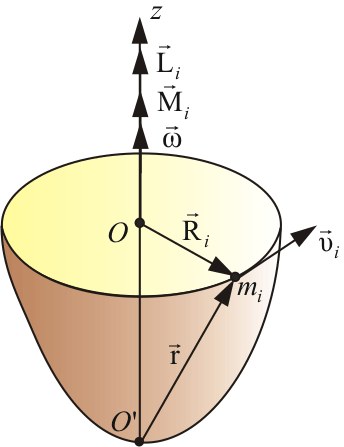

 Пусть некоторое тело вращается вокруг оси z.Получим уравнение динамики для некоторой точки mi этого тела находящегося на расстоянии Ri от оси вращения. При этом помним, что и
Пусть некоторое тело вращается вокруг оси z.Получим уравнение динамики для некоторой точки mi этого тела находящегося на расстоянии Ri от оси вращения. При этом помним, что и направлены всегда вдоль оси вращения z, поэтому в дальнейшем опустим значок z.
направлены всегда вдоль оси вращения z, поэтому в дальнейшем опустим значок z.




 Так как тело абсолютно твердое, то в процессе вращения miиRi останутся неизменными. Тогда:
Так как тело абсолютно твердое, то в процессе вращения miиRi останутся неизменными. Тогда: Обозначим Ii – момент инерции точки находящейся на расстоянии R от оси вращения:
Обозначим Ii – момент инерции точки находящейся на расстоянии R от оси вращения: Так как тело состоит из огромного количества точек и все они находятся на разных расстояниях от оси вращения, то момент инерции тела равен:
Так как тело состоит из огромного количества точек и все они находятся на разных расстояниях от оси вращения, то момент инерции тела равен:
 Просуммировав по всем i-ым точкам,
Просуммировав по всем i-ым точкам,
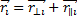
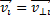



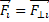
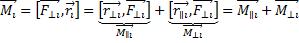
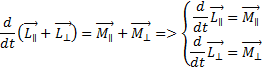
 )за счет сил трения в подшипниках всегда будет равняться нулю.
)за счет сил трения в подшипниках всегда будет равняться нулю.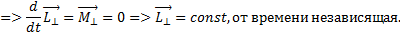

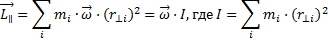

 – момент инерции.
– момент инерции.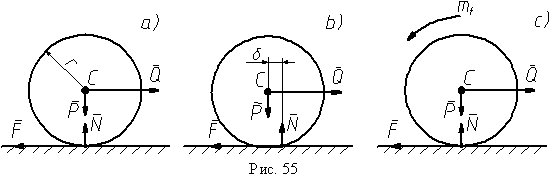
 (6)
(6)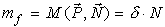 (7)
(7)