|
|
Скорость движения центра масс.
М — полная масса механической системы
k – некоторая система отсчета
18) Уравнение Мещерского. Реактивная сила. Уравнение Мещерского – основное уравнение в механике тел переменной массы, полученное Иваном Мещерским в 1904г. Является частным случаем второго закона Ньютона. Вывод формулы: В момент времени
Если
19) Центральные силы взаимодействия между частицами направлены вдоль линии, соединяющей эти частицы. Эти силы зависят от расстояния между частицами, а следовательно силы являются консервативными.
*Полная механическая энергия системы взаимодействующих частиц сохраняется, если полная работа силы трения (неконсервативных сил) равняется нулю.
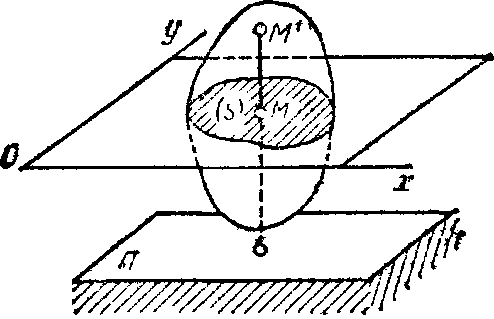
22) Поступательное, вращательное и плоскопараллельное движение твердого тела. Мгновенная ось вращения. Скорость точек при плоскопараллельном движении. Плоскопараллельным (или плоским) называется такое движение твердого тела, при, котором все его точки перемещаются параллельно некоторой фиксированной плоскости П(рис. 28). Плоское движение совершают многие части механизмов и машин, например катящееся колесо на прямолинейном участке пути, шатун в кривошипно-ползунном механизме и др. Частным случаем плоскопараллельного движения является вращательное движение твердого тела вокруг неподвижной оси.
Рис.28 Рис.29
Рассмотрим сечение Sтела какой-нибудь плоскости Оxy, параллельной плоскости П(рис.29). При плоскопараллельном движении все точки тела, лежащие на прямой ММ’, перпендикулярной течению S, т. е. плоскости П, движутся тождественно. Отсюда заключаем, что для изучения движения всего тела достаточно изучить, как движется в плоскости Оху сечение S этого тела или некоторая плоская фигураS. Поэтому в дальнейшем вместо плоского движения тела будем рассматривать движение плоской фигуры Sв ее плоскости, т.е. в плоскости Оху. Положение фигуры Sв плоскости Оху определяется положением какого-нибудь проведенного на этой фигуре отрезка АВ(рис. 28). В свою очередь положение отрезка АВможно определить, зная координаты При движении фигуры величины
Уравнения, определяющие закон происходящего движения, называются уравнениями движения плоской фигуры в ее плоскости. Они же являются уравнениями плоскопараллельного движения твердого тела. Первые два из уравнений движения определяют то движение, которое фигура совершала бы при Основными кинематическими характеристиками рассматриваемого движения являются скорость и ускорение поступательного движения, равные скорости и ускорению полюса
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
— импульсы частиц
масса тела 
, а ее скорость t wx:val="Cambria Math"/><w:i/><w:lang w:val="EN-US"/></w:rPr><m:t>v</m:t></m:r></m:e></m:acc></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 
; тогда по истечении времени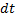 
его масса уменьшится на 
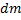и станет равной 
, а скорость увеличится до величины 
. Изменение импульса системы за время 
- внешние силы;
- скорость выбрасываемого тела;
– относительная скорость (скорость выбрасываемого тела относительно основного тела);
и 
точки Аи угол 
, который отрезок АВ образует с осью х. ТочкуА, выбранную для определения положения фигуры S, будем в дальнейшем называть полюсом.
и 
и 
будут изменяться. Чтобы знать закон движения, т. е. положение фигуры в плоскости Охув любой момент времени, надо знать зависимости
.
=const; это, очевидно, будет поступательное движение, при котором все точки фигуры движутся так же, как полюс А. Третье уравнение определяет движение, которое фигура совершала бы при 
и 
, т.е. когда полюсАнеподвижен; это будет вращение фигуры вокруг полюса А. Отсюда можно заключить, что в общем случае движение плоской фигуры в ее плоскости может рассматриваться как слагающееся из поступательного движения, при котором все точки фигуры движутся так же, как полюс А, и из вращательного движения вокруг этого полюса.
, 
, а также угловая скорость 
и угловое ускорение 
вращательного движения вокруг полюса.