
|
|
Консервативные силы. Связь консервативных сил с потенциальной энергией. Потенциальная энергия силы тяжести и упругой деформации.Ускорение точки при прямолинейном движении Если вектор
Частным случаем равноускоренного движения является случай, когда ускорение равно нулю в течение всего времени движения. В этом случае скорость постоянна, а движение происходит по прямолинейной траектории (если скорость тоже равна нулю, то тело покоится), поэтому такое движение называют прямолинейным и равномерным. Равноускоренное движение точки всегда является плоским, а твёрдого тела — плоскопараллельным (поступательным) Вектор ускорения
при движении точки по окружности можно разложить на два слагаемых (компоненты):
Тангенциальное ускорение —
Центростремительное или Нормальное ускорение
Угловое ускорение — показывает, на сколько изменилась угловая скорость за единицу времени, и, по аналогии с линейным ускорением, равно:
Направление вектора здесь показывает, увеличивается или уменьшается модуль скорости. Если векторы углового ускорения и скорости сонаправлены, значение скорости растёт, и наоборот.
4. Кривизна траектории показывает, какова форма движения в пространстве. Чтобы определить кривизну траектории, измеряют радиус кривизны. Если траектория является дугой окружности, радиус кривизны постоянный. С увеличением кривизны ее радиус уменьшается, и, наоборот, с уменьшением кривизны, радиус увеличивается. Пусть траетория имеет изгибы, тогда там где кусочек изгиба можно построить окружность подобранного радиуса, чтобы она подходила к данному месту изгиба. Радиус такой окружности и есть радиус кривизны. Формула для нахождения радиуса кривизны:
5) Вектор элементарного угла поворота, угловой скорости, углового ускорения. Центростремительное ускорение. Угловая скорость и угловое ускорение. Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени:
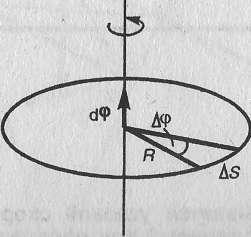
Вектор ω направлен вдоль оси вращения по правилу правого винта, т. е. так же, как и вектор dφ (рис. 2). Размерность угловой скорости dim ω = Т-1, а ее единица — радиан в секунду (рад/с). Линейная скорость точки (см. рис. 1)
Рис.1
т.е v=ωR
В векторном виде формулу для линейной скорости можно написать как векторное произведение:
При этом модуль векторного произведения, по определению, равен ωRsin(ω, R), а направление совпадает с направлением поступательного движения правого винта его вращения отω к R.
Рис.2
Если ω=const, то вращение равномерное и его можно характеризовать периодом вращения Т - временем, за которое точка совершает один полный оборот, т. е. поворачивается на угол 2π. Так как промежутку времени Δt=Т соответствует Δφ=2π, то ω=2π/T, откуда Т = 2π/ω.
Число полных оборотов, совершаемых телом при равномерном его движении по окружности, в единицу времени называется частотой вращения: n= 1/T = ω/(2π),
ω = 2πn.
Рис.3
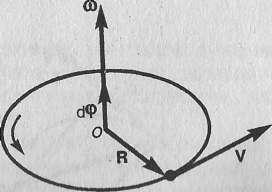
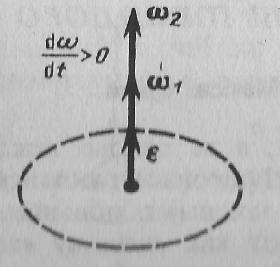
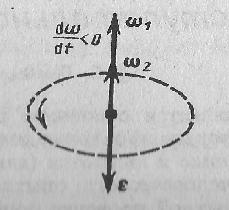
При вращении тела вокруг неподвижной оси вектор углового ускорения ε направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном движении вектор εсонаправлен вектору ω (рис. 3), при замедленном - противонаправлен ему (рис. 4).
Рис.4
Тангенциальная составляющая ускорения aτ=dv/dt , v = ωR и
Нормальная составляющая ускорения
Значит, связь между линейными (длина пути s, пройденного точкой по дуге окружности радиуса R, линейная скорость v, тангенциальное ускорение аτ, нормальное ускорение аn) и угловыми величинами (угол поворота φ, угловая скорость ω, угловое ускорение ε) выражается следующими формулами: s = Rφ, v = Rω, аτ = R?, an = ω2R.
В случае равнопеременного движения точки по окружности (ω=const) ω = ω0 ± ?t, φ = ω0t ± ?t2/2,
где ω0 — начальная угловая скорость.
6. Угловая скорость – векторная величина, определяемая первой производной угла поворота тела по времени. Выражается формулой Угловое ускорение – векторная величина, определяемая первой производной угловой скорости по времени. Выражается формулой Связь между угловыми величинами ( угловой скоростью и угловым ускорением) с линейными (линейной скоростью, тангенциального и линейного ускорения) выражается следующими формулами :
7. Равноускоренное прямолинейное движение. В общем случаеравноускоренным движением называют такое движение, при котором вектор ускорения Определяется по формулам:
8 . Движение тела по окружности является частным случаем криволинейного движения. Наряду с вектором перемещения Угловая скорость измеряется в рад/с. Связь между модулем линейной скорости υ и угловой скоростью ω:
При равномерном движении тела по окружности величины υ и ω остаются неизменными. В этом случае при движении изменяется только направление вектора Равномерное движение тела по окружности является движением с ускорением. Ускорение
направлено по радиусу к центру окружности. Его называют нормальным, или центростремительным ускорением. Модуль центростремительного ускорения связан с линейной υ и угловой ω скоростями .
9. Основные Законы и принцип механики Ньютона 1 закон Ньютона Если ускорение тела равно 0,то существуют такие системы координат в которых это тело будет иметь простейшее уравнение движения, то есть двигаться прямолинейно и равномерно, либо покоится. 2 Закон Ньютона(самый основной) Зависимость вектора ускорения от вектора силы согласно Ньютону, вектор ускорения прямопропорционален вектору силы и обратно пропорционален массе тела. 3 Закон Ньютона Описывает взаимодействие между телами и утверждает что сила которая действует на 1-ое тело со стороны 2-ого по величине равен вектору силы действующей со стороны 1-ого тела. Основной принцип: Масса тела не зависит от скорости тела, не зависит от его положения в пространстве, а также от взаимодействия с другими телами. (масса яв-ся характеристикой).
10) Закон всемирного тяготения. Сила тяжести. Вес тела. Невесомость.
Всемирное тяготение Ньютон обобщил законы движения небесных тел и выяснил, Сила тяжести Частным видом силы всемирного тяготения является сила притяжения тел к Земле. Эту силу называют силой тяжести. Под действием этой силы все тела приобретают ускорение свободного падения. В соответствии со вторым законом Ньютона g = Ft*m следовательно, Ft = mg. Сила тяжести всегда направлена к центру Земли. В зависимости от высоты h над поверхностью Земли и географической широты положения тела ускорение свободного падения приобретает различные значения. На поверхности Земли и в средних широтах ускорение свободного падения равно 9,831 м/с2.
(РЕБЯТА! Убедительная просьба, для вас лучше будет . НЕ СМЕЙТЕ говорить , что вес тела – это масса.) Невесомость 11.Упругие силы Силы упругости При деформациях твердого тела его частицы (атомы, молекулы, ионы), находящиеся в узлах кристаллической решетки, смещаются из своих положений равновесия. Этому смещению противодействуют силы взаимодействия между частицами твердого тела, удерживающие эти частицы на определенном расстоянии друг от друга. Поэтому при любом виде упругой деформации в теле возникают внутренние силы, препятствующие его деформации. Силы, возникающие в теле при его упругой деформации и направленные против направления смещения частиц тела, вызываемого деформацией, называют силами упругости. Силы упругости действуют в любом сечении деформированного тела, а также в месте его контакта с телом, вызывающим деформации. В случае одностороннего растяжения или сжатия сила упругости направлена вдоль прямой, по которой действует внешняя сила, вызывающая деформацию тела, противоположно направлению этой силы и перпендикулярно поверхности тела. Природа упругих сил электрическая. ОБЪЁМНАЯ ДЕФОРМАЦИЯ:При деформации объем тела изменяется. Рассмотрим бесконечно малый параллелепипед объемом ДЕФОРМАЦИЯ СДВИГА:При деформации сдвига происходит сдвиг атомных плоскостей относительно других атомных плоскостей. Относительная деформация сдвига определяется по формуле: где Δx — абсолютный сдвиг параллельных слоёв тела относительно друг друга; l — расстояние между слоями ( Закон Гука для упругих деформаций Закон Гука Связь между силой упругости и упругой деформацией тела (при малых деформациях) была экспериментально установлена современником Ньютона английским физиком Гуком. Математическое выражение закона Гука для деформации одностороннего растяжения (сжатия) имеет вид f=-kx:где f - сила упругости; х - удлинение (деформация) тела; k - коэффициент пропорциональности, зависящий от размеров и материала тела, называемый жесткостью. Единица жесткости в СИ - ньютон на метр (Н/м). Закон Гука для одностороннего растяжения (сжатия) формулируют так: сила упругости, возникающая при деформации тела, пропорциональна удлинению этого тела. Тангенциальное и нормальное напряжение Механическое напряжение — это мера внутренних сил, возникающих в деформируемом теле под влиянием различных факторов. Механическое напряжение в точке тела определяется как отношение внутренней силы к единице площади в данной точке рассматриваемого сечения.
Напряжения являются результатом взаимодействия частиц тела при его нагружении. Внешние силы стремятся изменить взаимное расположение частиц, а возникающие при этом напряжения препятствуют смещению частиц, ограничивая его в большинстве случаев некоторой малой величиной.
Q — механическое напряжение. F — сила, возникшая в теле при деформации. S — площадь. Различают две составляющие вектора механического напряжения: Нормальное механическое напряжение — приложено на единичную площадку сечения, по нормали к сечению (обозначается σ). Касательное механическое напряжение — приложено на единичную площадку сечения, в плоскости сечения по касательной (обозначается τ). Совокупность напряжений, действующих по различным площадкам, проведенным через данную точку, называется напряженным состоянием в точке. В системе СИ механическое напряжение измеряется в паскалях.
13.Работа- скалярная физическая величина, равная произведению модуля силы на модуль перемещения и на косинус угла между ними.
Где
Мощность--скалярная физическая величина, численно равная отношению работы, совершаемой за некоторый промежуток времени, к этому промежутку времени.
Кинетическая энергия-скалярная физическая величина, численно равная половине произведения массы частицы на квадрат модуля ее скорости.
Кинетическая энергия системы отсчета равна сумме кинетических энергий входящих в нее частиц.
где
Теорема о кинетической энергии: Работа равнодействующей силы равна превращению кинетической энергии тела.
14. Консервативные силы. Связь консервативных сил с потенциальной энергией. Потенциальная энергия силы тяжести и упругой деформации.
Сила, действующая на материальную точку, называется консервативной (потенциальной), если работа этой силы зависит только от начального и конечного положений точки. Работа консервативной силы не зависит ни от вида траектории, ни от закона движения материальной точки по траектории Работа консервативных сил равна убыли потенциальной энергии Если в системе действуют консервативные силы, то система обладает потенциальной энергией поэтому консервативные силы называют потенциальными А = Еп1 – Еп2 = -ΔЕпот Потенциальная энергия упруго деформированного тела. Физическая величина, равная половине произведения жесткости тела на квадрат его деформации, называется потенциальной энергией упруго деформированного тела:
Потенциальная энергия упруго деформированного тела — это энергия взаимодействия отдельных частей тела между собой силами упругости. Потенциальная энергия поднятого над Землей тела — это энергия взаимодействия тела и Земли гравитационными силами. Ep=mgh Потенциальная энергия тела в поле силы тяжести.
15)Импульс системы частиц. Теорема об изменении импульса системы частиц Импульсом системы частиц называется суммарный импульс всех частиц системы, т.е.
Используя определение центра инерции системы (4.4) и его скорости, выражение для импульса системы частиц можно преобразовать к виду
где
- скорость изменения импульса системы частиц равна главному вектору внешних сил, действующих на частицы системы. Если главный вектор внешних сил равен нулю, то импульс системы частиц сохраняется (закон сохранения импульса системы частиц). Закон сохранения импульса для системы частиц. Если на систему взаимодействия частиц не действуют никакие внешние силы F, или эта результирующая сила = 0, тогда суммарный импульс такой системы не будет зависеть от времени 16. Упругое и неупругое соударение тел Удар упругий- это такой удар при котором механическая энергия взаимодействия тел не сохраняется. Неупругий удар- когда часть механической энергии переходит в др. виды энергии. (Например в тепловую).
17.Центр масс– геометрическая точка, характеризующая движение тела или системы частиц как целого. Движение твёрдого тела можно рассматривать как суперпозицию движения центра масс и вращательного движения тела вокруг его центра масс. Центр масс при этом движется так же, как двигалось бы тело с такой же массой, но бесконечно малыми размерами (материальная точка). Для описания этого движения применимы все законы Ньютона. Во многих случаях можно вообще не учитывать размеры и форму тела и рассматривать только движение его центра масс.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 не меняется со временем, движение называют равноускоренным. При равноускоренном движении справедливы формулы:
не меняется со временем, движение называют равноускоренным. При равноускоренном движении справедливы формулы: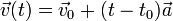
 .
.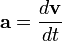
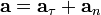
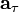 направлено по касательной к траектории (обозначается иногда
направлено по касательной к траектории (обозначается иногда 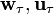 в зависимости от того, какой буквой в данной книге принято обозначать ускорение). Является составляющей вектора ускорения a. Характеризует изменение скорости по модулю.
в зависимости от того, какой буквой в данной книге принято обозначать ускорение). Является составляющей вектора ускорения a. Характеризует изменение скорости по модулю.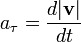
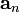 — возникает (не равно нулю) всегда при движении точки по окружности (конечного радиуса) (также обозначается иногда
— возникает (не равно нулю) всегда при движении точки по окружности (конечного радиуса) (также обозначается иногда 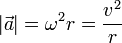
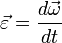
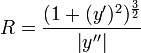
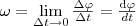
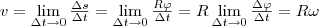
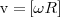
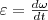
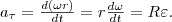
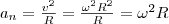
 =
= 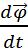 .
. .
. - где:
- где:  – линейная скорость точки.
– линейная скорость точки. - где:
- где:  - тангенциальное ускорение,
- тангенциальное ускорение, 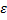 - угловое ускорение.
- угловое ускорение. - где:
- где:  – нормальное ускорение.
– нормальное ускорение. остается неизменным по модулю и направлению. Примером такого движения является движение камня, брошенного под некоторым углом к горизонту (без учета сопротивления воздуха). В любой точке траектории ускорение камня равно ускорению свободного падения
остается неизменным по модулю и направлению. Примером такого движения является движение камня, брошенного под некоторым углом к горизонту (без учета сопротивления воздуха). В любой точке траектории ускорение камня равно ускорению свободного падения .
.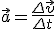
 .
.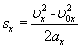
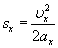
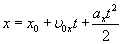
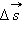 удобно рассматривать угловое перемещение Δφ (или угол поворота), измеряемое в радианах
удобно рассматривать угловое перемещение Δφ (или угол поворота), измеряемое в радианах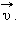


 Силы всемирного тяготения действуют между любыми телами в природе, но ощутимыми они становятся при больших массах.
Силы всемирного тяготения действуют между любыми телами в природе, но ощутимыми они становятся при больших массах.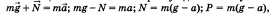 (не важно)
(не важно)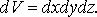 С точностью до бесконечно малых высшего порядка можно считать, что изменение объема обусловлено только изменением длины ребер и не связано с изменением углов сдвига.
С точностью до бесконечно малых высшего порядка можно считать, что изменение объема обусловлено только изменением длины ребер и не связано с изменением углов сдвига. ,
, для малых углов )
для малых углов )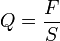
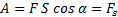
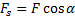 - проекция силы
- проекция силы  на направление перемещения
на направление перемещения 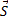 .
.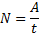

 (через импульс)
(через импульс)
 -масса системы
-масса системы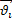 – скорость i-ой частицы относительно центра масс,
– скорость i-ой частицы относительно центра масс, 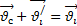
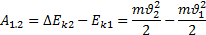
 .
.
 . (4.6)
. (4.6) , (4.7)
, (4.7) - масса системы и
- масса системы и  - скорость центра инерции. Дифференцируя (4.7) по времени и используя (4.5), получим теорему об изменении импульса системы частиц:
- скорость центра инерции. Дифференцируя (4.7) по времени и используя (4.5), получим теорему об изменении импульса системы частиц: (4.8)
(4.8)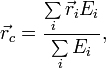
 — радиус-вектор центра масс,
— радиус-вектор центра масс, — радиус-вектор i-й частицы системы,
— радиус-вектор i-й частицы системы,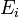 — полная энергия i-й частицы.
— полная энергия i-й частицы.