
|
|
Скалярное произведение векторовОпределение 11. Скалярным произведением двух ненулевых векторов
Если хотя бы один из них равен нулевому вектору, то их скалярное произведение считается равным нулю. Угол между векторами Для скалярного произведения наряду с обозначением Геометрические свойства скалярного произведения: 1) 2) если Алгебраические свойства скалярного произведения: 1) 2) 3) Если векторы
Отсюда, в частности, следует формула для определения косинуса угла между векторами:
Векторное произведение векторов Определение 12. Упорядоченная тройка некомпланарных векторов 1) если, будучи приведены к общему началу, эти векторы располагаются так, как могут быть расположены соответственно большой, несогнутый указательный и средний пальцы правой (левой) руки; 2) если после приведения к общему началу вектор 3) если, находясь внутри телесного угла, образованного приведёнными к общему началу векторами По договорённости обычно рассматривают только правые системы координат. Например, тройка базисных векторов прямоугольной декартовой системы координат в Определение 13. Векторным произведением вектора 1) длина вектора 2) вектор 3) вектор Из определения следует, что если хотя один из них равен 0 или они коллинеарны, то Алгебраические свойства векторного произведения: 1) 2) 3) 4) Если
или в символической записи
Данный определитель нужно раскладывать по элементам первой строки. Смешанное произведение векторов Определение 14. Смешанным произведением упорядоченной тройки векторов Геометрические свойства смешанного произведения: 1) если
2) для того, чтобы три вектора Смешанное произведение через координаты векторов в прямоугольном базисе записывается в виде:
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 1. Известно, что: Вычислить: а) Решение. а) По определению скалярного произведения двух векторов:
При решении б) и в) пользовались алгебраическими свойствами и определением скалярного произведения. Задача 2. Даны векторы б) Решение. а) Воспользуемся формулой (6).
б) Вычислим сначала координаты векторов
Воспользуемся формулой (6):
в) Найдём сначала координаты вектора
г) Найдём координаты вектора
По формуле (5) находим:
Ответ. а) Задача 3. При каком значении Решение. Т.к. Решаем квадратное уравнение относительно
Таким образом, мы получили два значения Задача 4. Найти угол между векторами Решение. По формуле (7) для определения косинуса угла между двумя векторами будем иметь Найдём сначала
Вычислим теперь длины векторов
Ответ. Задача 5. Известно, что Вычислить: а) Решение. а) Воспользуемся определением векторного произведения:
б) С учётом 1-го и 2-го свойства векторного произведения получаем:
в) По определению векторного произведения находим:
Ответ. а) Задача 6. Заданы векторы Решение. а) Т.к. векторы
Мы получили разложение вектора векторного произведения в прямоугольном базисе или б) Вычислим координаты вектора
По формуле (8) находим:
=
Можно было найти координаты вектора
в) Вычислим координаты векторов
По формуле (8) находим:
=
Или, если учитывать результат пункта а):
Ответ. а) в) Задача 7. Вычислить площадь параллелограмма, построенного на векторах Решение. Так как площадь параллелограмма, построенного на векторах
где Задача 8. Вычислить площадь треугольника с вершинами Решение. Площадь треугольника находится по формуле:
Поэтому найдём
Ответ. Задача 9. Найти объём тетраэдра, построенного на векторах Решение. Отметим, что объём тетраэдра, построенного на трёх заданных векторах
откуда
Задача 10. В тетраэдре с вершинами в точках Решение. Из курса геометрии известно, что объём тетраэдра находится по формуле:
Объём тетраэдра равен
откуда
1.3 ПРЯМАЯ НА ПЛОСКОСТИ Справедливо следующее утверждение: если на плоскости Уравнение
с произвольными коэффициентами В курсе аналитической геометрии доказывается, что прямая, определяемая общим уравнением (10), перпендикулярна вектору Каноническим уравнением прямой называется уравнение вида
или
Уравнение (11) – уравнение прямой, проходящей через заданную точку Уравнение (12) – уравнение прямой, проходящей через две данные точки Уравнением прямой с угловым коэффициентом называется уравнение
где Уравнение прямой, не проходящей через начало координат и пересекающей оси координат в точках
Если заданы произвольная точка
где Уравнение прямой, проходящей через заданную точку
Пусть
Уравнение (17) называется нормальным уравнением прямой. Общее уравнение прямой (10) приводится к виду (17) путём умножения на нормирующий множитель
В результате получается
Знак нормирующего множителя противоположен знаку Расстояние
Если две прямые
то косинус угла
Условие параллельности прямых
Условие перпендикулярности прямых
Если известны координаты направляющих векторов Если прямые
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 1. Записать уравнение прямой, проходящей через точку Решение. Воспользуемся уравнением (11), тогда уравнение прямой будет иметь вид:
Задача 2. Составить уравнение прямой, проходящей через две точки Решение. Воспользуемся каноническим уравнением прямой (12):
Подставляя вместо
Уравнение прямой можно записать в общем виде:
Задача 3. Составить уравнение прямой, проходящей через начало координат и наклонённой к оси Решение. Так как прямая проходит через начало координат, то в уравнении
Задача 4. Написать уравнение прямой, проходящей через точку Решение. Уравнение прямой запишем в виде (16):
По условию задачи
Раскрыв скобки, получим общее уравнение прямой:
Задача 5. Написать параметрические уравнения прямой, проходящей через точку Решение. Воспользуемся формулами (15):
Задача 6. Составить уравнение прямой, отсекающей на осях координат отрезки 3 и 5. Решение. Воспользуемся формулой (14). Уравнение прямой в отрезках на осях:
Задача 7. Записать уравнение прямой Решение. Разделим обе части уравнения на (-5):
Здесь Задача 8. Определить площадь треугольника, заключённого между осями координат и прямой Решение. Данный треугольник – прямоугольный, катеты которого представляют собой отрезки, отсекаемые прямой на координатных осях. Запишем уравнение
Здесь Задача 9. Заданы прямая 1) вычислить расстояние 2) написать уравнение прямой 3) написать уравнение прямой Решение. 1) Расстояние от точки
2) Нормальный вектор заданной прямой Подставляя координаты точки
3) По условию задачи прямая
Подставляя координаты точки
Ответ. 1) Задача 10. Установить взаимное расположение прямых Решение. Условия параллельности и перпендикулярности прямых не выполняются. Вектор нормали первой прямой имеет координаты
Следовательно, прямые пересекаются. Точка пересечения принадлежит и первой и второй прямой. Её координаты найдём из системы уравнений:
Отсюда получаем Задача 11. Треугольник 1) Написать уравнение стороны 2) Написать уравнение высоты 3) Найти угол Решение. 1) Воспользуемся уравнением прямой, проходящей через две заданные точки (12):
2) Уравнение высоты Нормальный вектор прямой
Раскрыв скобки, получим уравнение высоты
Длина
3) По определению медианы точка
Таким образом, Составим уравнение медианы
Чтобы найти угол между высотой
Подставим координаты данных векторов в уравнение (7):
Ответ. 1) 3) Задача 12. Определить положение точки Решение. Подставим координаты точки
Задача 13. Написать уравнение прямой, проходящей через точку Решение. Прямая

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 и
и 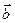 называют число
называют число .
. – наименьший угол между ними.
– наименьший угол между ними. используется также
используется также  .
. (условие перпендикулярности векторов);
(условие перпендикулярности векторов); , то
, то  и
и 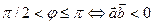 .
. (коммутативность);
(коммутативность); (ассоциативность);
(ассоциативность); (дистрибутивность).
(дистрибутивность). и
и 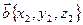 представлены своими координатами в прямоугольном базисе, то скалярное произведение равно:
представлены своими координатами в прямоугольном базисе, то скалярное произведение равно: . (6)
. (6) . (7)
. (7) называется правой (левой), если выполнено одно из следующих трёх условий:
называется правой (левой), если выполнено одно из следующих трёх условий: располагается по ту сторону плоскости векторов
располагается по ту сторону плоскости векторов  и
и  , откуда кратчайший поворот от
, откуда кратчайший поворот от  , мы видим поворот от
, мы видим поворот от  является правой.
является правой.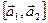 (или
(или 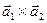 ), определяемый следующими тремя условиями:
), определяемый следующими тремя условиями: ;
;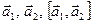 правая.
правая. .
. ;
; ;
; ;
; .
. и
и  - векторы, заданные своими координатами в базисе
- векторы, заданные своими координатами в базисе  , то разложение векторного произведения
, то разложение векторного произведения  ,
, . (8)
. (8) , которое обозначается
, которое обозначается 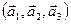 .
. объём параллелепипеда, построенного на векторах
объём параллелепипеда, построенного на векторах 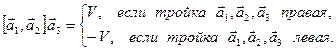
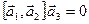 .
. . (9)
. (9)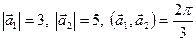 .
.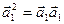 , б)
, б)  , в)
, в)  .
. , т.е.
, т.е.  . Таким образом, получили, что скалярное произведение вектора на себя равно квадрату его длины:
. Таким образом, получили, что скалярное произведение вектора на себя равно квадрату его длины: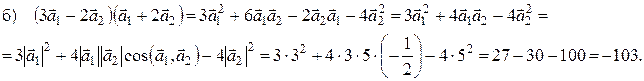
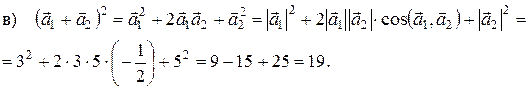
 и
и  . Вычислить: а)
. Вычислить: а)  ;
; ; в)
; в)  ; г)
; г)  .
. ;
;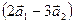 и
и  .
.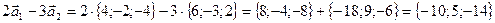 ;
; ;
;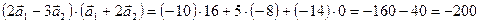 ;
; .
. ;
; ;
; .
. ;
; .
. ; б)
; б)  ; в)
; в)  ; г)
; г)  .
. векторы
векторы  и
и  перпендикулярны?
перпендикулярны? , то имеем:
, то имеем: 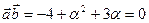 .
.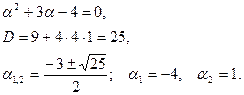
 и
и  , где
, где  и
и  -единичные взаимно перпендикулярные векторы.
-единичные взаимно перпендикулярные векторы. .
. :
: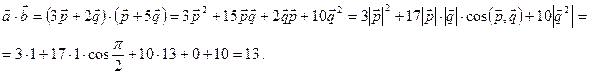


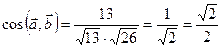 .
. .
. .
. ; б)
; б)  ; в)
; в)  .
. ;
; .
. .
. ;
;
 ;
; ; б)
; б)  ; в)
; в)  .
. и
и  . Найти координаты векторов: а)
. Найти координаты векторов: а)  ; в)
; в)  .
.
 .
. :
: .
.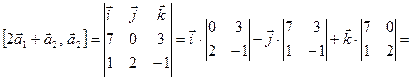
 .
. .
.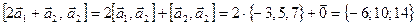 .
. и
и  .
. .
.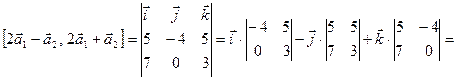
 .
. .
. .
. ; б)
; б)  ,
,  .
. , а затем вычислим длину полученного вектора.
, а затем вычислим длину полученного вектора.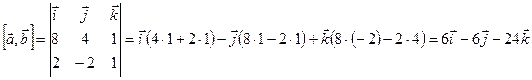 .
.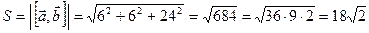 (ед2),
(ед2), площадь параллелограмма.
площадь параллелограмма. ,
,  и
и  .
. .
.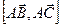 , а затем вычислим длину полученного вектора.
, а затем вычислим длину полученного вектора. ;
;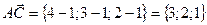 ;
; .
. ,
, (ед2).
(ед2). (ед2).
(ед2). ,
,  ,
,  .
. .
. ,
, (ед3).
(ед3). ,
,  ,
,  ,
,  вычислить высоту
вычислить высоту  .
.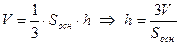 .
. . Найдём координаты векторов
. Найдём координаты векторов 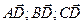 .
. ,
, ,
,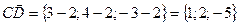 ,
, ,
,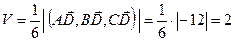 (ед3).
(ед3).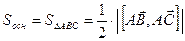 .
. ;
; ;
; .
. .
. ,
, (ед2).
(ед2). (ед.).
(ед.). фиксирована произвольная декартова прямоугольная система координат
фиксирована произвольная декартова прямоугольная система координат  , то всякое уравнение первой степени с двумя переменными
, то всякое уравнение первой степени с двумя переменными  и
и  (линейное уравнение) определяет относительно этой системы координат прямую линию.
(линейное уравнение) определяет относительно этой системы координат прямую линию. (10)
(10) и
и  таким, что
таким, что  и
и  не равны нулю одновременно, называется общим уравнением прямой.
не равны нулю одновременно, называется общим уравнением прямой. . Этот вектор называется нормальным вектором прямой (10).
. Этот вектор называется нормальным вектором прямой (10). , (11)
, (11) , (12)
, (12) , параллельно некоторому вектору
, параллельно некоторому вектору  , который называется направляющим вектором прямой.
, который называется направляющим вектором прямой. и
и  .
. , (13)
, (13) угловой коэффициент, равный тангенсу угла наклона прямой к положительному направлению оси
угловой коэффициент, равный тангенсу угла наклона прямой к положительному направлению оси  ордината точки
ордината точки 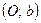 , в которой прямая, не параллельная оси
, в которой прямая, не параллельная оси 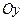 , пересекает эту ось.
, пересекает эту ось. и
и  , может быть записано в виде (уравнение в отрезках на осях):
, может быть записано в виде (уравнение в отрезках на осях): . (14)
. (14) , то параметрические уравнения прямой, проходящей через данную точку, параллельно данному вектору, имеют вид:
, то параметрические уравнения прямой, проходящей через данную точку, параллельно данному вектору, имеют вид: (15)
(15) .
. . (16)
. (16) угол от положительного направления оси
угол от положительного направления оси  до луча
до луча  , проходящего через начало координат, перпендикулярного к прямой и пересекающего эту прямую, а
, проходящего через начало координат, перпендикулярного к прямой и пересекающего эту прямую, а  расстояние от начала координат до прямой. Тогда уравнение прямой может быть записано в виде:
расстояние от начала координат до прямой. Тогда уравнение прямой может быть записано в виде: . (17)
. (17)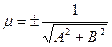 .
.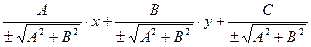 .
. , то знак
, то знак 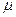 выбирается произвольным образом.
выбирается произвольным образом. от точки
от точки  до прямой, заданной общим уравнением (10) определяется по формуле:
до прямой, заданной общим уравнением (10) определяется по формуле: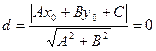 . (18)
. (18)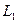 и
и  заданы уравнениями:
заданы уравнениями: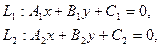
 между ними определяется по формуле:
между ними определяется по формуле: . (19)
. (19) и
и  , эквивалентно условию коллинеарности векторов
, эквивалентно условию коллинеарности векторов  и
и  , заключается в пропорциональности координат этих векторов, то есть имеет вид:
, заключается в пропорциональности координат этих векторов, то есть имеет вид: . (20)
. (20) . Оно имеет вид:
. Оно имеет вид: . (21)
. (21) и
и  , то условия параллельности и перпендикулярности прямых записываются аналогично условиям (20) и (21) соответственно.
, то условия параллельности и перпендикулярности прямых записываются аналогично условиям (20) и (21) соответственно. . (22)
. (22) , параллельно вектору
, параллельно вектору  .
. .
.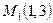 и
и  .
. и
и  координаты точек
координаты точек  и
и 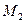 соответственно, получим:
соответственно, получим: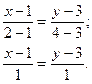
 .
. . Уравнение прямой будет иметь вид
. Уравнение прямой будет иметь вид  . Так как
. Так как  , то окончательно получаем:
, то окончательно получаем: .
. перпендикулярно вектору
перпендикулярно вектору  .
.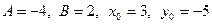 .
. .
. .
. параллельно вектору
параллельно вектору  .
. ,
, .
. .
. в отрезках на осях.
в отрезках на осях. ,
,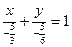 .
. .
. .
.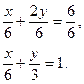
 .
.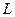 :
:  и точка
и точка  . Требуется:
. Требуется: от точки
от точки  до прямой
до прямой  , проходящей через точку
, проходящей через точку  , проходящей через точку
, проходящей через точку  . Подставляя эти значения в данную формулу, получим:
. Подставляя эти значения в данную формулу, получим: .
.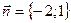 . Так как прямая
. Так как прямая  прямой
прямой 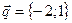 .
. ;
; ;
; ;
;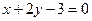 .
. .
. ;
;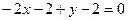 ;
;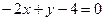 ;
;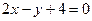 .
. ; 2)
; 2)  и
и  . Если прямые пересекаются, найти их точку пересечения.
. Если прямые пересекаются, найти их точку пересечения. , второй прямой –
, второй прямой –  .
. и
и  .
.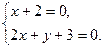
 ,
, 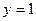 . Точка пересечения имеет координаты
. Точка пересечения имеет координаты  .
.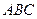 задан координатами своих вершин:
задан координатами своих вершин:  ,
,  и
и  . Требуется:
. Требуется: ;
;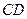 , опущенной из вершины
, опущенной из вершины  ;
; .
.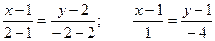 ;
; ;
;  ;
; .
.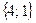 можно взять в качестве направляющего вектора искомой прямой, так как он будет ей перпендикулярен. Подставляя координаты вектора
можно взять в качестве направляющего вектора искомой прямой, так как он будет ей перпендикулярен. Подставляя координаты вектора  :
:  ;
; .
. .
. это расстояние от точки
это расстояние от точки  .
. середина отрезка
середина отрезка  . Её координаты находятся по следующим формулам:
. Её координаты находятся по следующим формулам:  . Подставляя координаты точек
. Подставляя координаты точек  .
. .
.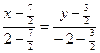 ;
; ;
; ;
;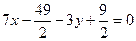 ;
; .
.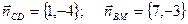 .
. .
.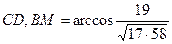 .
. ;
; относительно прямой
относительно прямой  .
. . Следовательно, пара чисел не является решением уравнения
. Следовательно, пара чисел не является решением уравнения  под углом
под углом  к прямой
к прямой 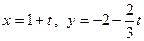 .
. ,
,  . Подставим данные значения в (11):
. Подставим данные значения в (11): ;
;