
|
|
Линейные операции над векторамиМЕТОДИЧЕСКИЕ УКАЗАНИЯ к самостоятельной работе по математике
Часть 1 Аналитическая геометрия
для студентов 1 курса всех специальностей заочной и дистанционной форм обучения
ШАХТЫ 2003
СОСТАВИТЕЛИ
Грозина А.А. доцент кафедры математики, к. т. н.
Саакян О.В. ассистент кафедры математики
Скрипочка Л.Н. ассистент кафедры математики
Хоменко Ю.А. доцент кафедры математики, к.с.н.
РЕЦЕНЗЕНТЫ
Саакян Г.Р. доцент кафедры математики к.т.н. Охрименко О.И. доцент кафедры математики, к.э.н.
Методические указания предназначены студентам заочной и дистанционной форм обучения для подготовки к сдаче экзаменов, выполнению контрольных работ по дисциплине «Математика». Содержат теоретический материал по теме «Аналитическая геометрия», образцы решения примеров. Данные методические указания могут быть также использованы и студентами дневной формы обучения при самостоятельном изучении данной темы, при подготовке к сдаче контрольных точек.
СОДЕРЖАНИЕ
Введение 4 1 Аналитическая геометрия 4 1.1 Определители и матрицы 4 Примеры решения задач 6 1.2 Элементы векторной алгебры 8 Примеры решения задач 12 1.3 Прямая на плоскости 17 Примеры решения задач 19 1.4 Уравнения прямой и плоскости в пространстве 24 Примеры решения задач 27 Список использованных источников 31
Данные методические указания содержат достаточно большое количество задач с решениями по аналитической геометрии, наиболее часто встречающихся в аудиторных контрольных работах для студентов первого курса заочного факультета всех специальностей. В данной работе приводятся также теоретические справки по каждому разделу. Приведённая в методических указаниях теоретическая часть позволит использовать их при самостоятельной работе по изучению указанных тем, при подготовке к сдаче экзаменов студентами заочной формы обучения всех специальностей. В конце методических указаний приводится список рекомендуемой и используемой литературы.
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
1.1 ОПРЕДЕЛИТЕЛИ И МАТРИЦЫ Прежде чем ввести понятие определителя, дадим определение матрицы. Определение 1. Прямоугольная таблица чисел, состоящая из
задающее матрицу
Если Рассмотрим квадратную матрицу второго порядка.
и дадим определение определителя матрицы второго порядка. Определение 2. Выражение
Дадим теперь понятие определителя третьего порядка (или определителя матрицы размера
Отметим правило для построения выражения (2). Выделим в этом определителе главную диагональ, образованную числами
На рисунке 1 это правило изображено схематически. Рассмотрим теперь определитель
Определение 3. Минором Теорема 1. Каков бы ни был номер строки
Поэтому все определители порядка
Следует отметить, что правила (3), (4) выгодно применять, если определитель имеет строку (столбец), в которой лишь небольшое количество элементов отлично от нуля. В этом случае, раскрывая определитель по этой строке (столбцу), мы получим в правой части формул (3), (4) небольшое количество слагаемых. Свойства определителей 10. При перемене местами двух строк (или столбцов) определителя его знак меняется на противоположный, а абсолютная величина не меняется. 20. Определитель с двумя одинаковыми строками или столбцами равен нулю. 30. Умножение всех элементов некоторой строки (или столбца) определителя на число λ, равносильно умножению определителя на это число, т.е. постоянный множитель можно выносить за знак определителя из любой строки или любого столбца. 40. Если все элементы некоторой строки (или столбца) равны нулю, то определитель равен нулю. 50. Если элементы двух строк (или столбцов) определителя пропорциональны, то определитель равен нулю. 60. Если к элементам некоторой строки (или столбца) определителя прибавить соответствующие элементы другой строки (столбца), умноженные на действительное число λ, то величина определителя не изменится.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Пример 1. Найти определитель матрицы Решение.
Пример 2. Вычислить определитель: Решение.
Пример 3. Решить уравнение: Решение. Вычислим определитель:
Ответ. -4; -1. Пример 4. Решить уравнение: Решение. Вычислим определитель:
При решении воспользовались формулой:
Ответ. Пример 5. Вычислить определитель 3-го порядка Решение. Вычислим данный определитель по правилу (2).
Пример 6. Вычислить определитель Решение. Данный определитель можно вычислить и по правилу (2), но так как первый столбец определителя содержит два нуля, то целесообразней разложить данный определитель по элементам первого столбца:
Пример 7. Вычислить определитель Решение. В данном определителе нет нулевых элементов, поэтому вычислим его по правилу (2).
Пример 8. Решить неравенство: Решение. Вычислим сначала определитель, используя правило (2).
Далее решаем неравенство
Ответ. Пример 9. Вычислить определитель 4-го порядка, используя разложение по элементам первой строки: Решение. Используя формулу (3), разложим данный определитель по первой строке:
Здесь определители третьего порядка представляют собой миноры
1.2 ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
Пусть на плоскости дана декартова прямоугольная система координат. Из школьного курса геометрии известно, что каждая точка Аналогично, каждой точке В геометрии вектором (геометрическим) В аналитической геометрии рассматривают пространство «свободных» векторов, т.е. отождествляют (считают равными) любые два вектора, которые совпадают, если при параллельном переносе совместить их начала. Поэтому мы можем всё пространство таких «свободных» векторов отождествить с пространством векторов, исходящих из начала координат. Определение 4. Длиной вектора
Определение 5. Вектор называется нулевым, если начало и конец его совпадают, т.е. его длина равна 0. Определение 6. Векторы называются коллинеарными, если они лежат на одной прямой, либо на параллельных прямых. Определение 7. Два вектора Определение 8. Векторы называются компланарными, если существует плоскость, которой они параллельны. Линейные операции над векторами Линейными операциями над векторами принято называть операцию сложения векторов и операцию умножения векторов на вещественные числа. Сумма векторов
Произведение вектора
Определение 9. Векторы Определение 10. Три линейно независимых вектора
При этом числа В случае декартовой прямоугольной системы координат базисные векторы принято обозначать буквами Выражение
означает, что имеется вектор 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ВВЕДЕНИЕ
ВВЕДЕНИЕ строк и
строк и  столбцов, называется матрицей размера
столбцов, называется матрицей размера  . Используется обозначение
. Используется обозначение ,
, размера
размера  той строки и
той строки и  го столбца находится число
го столбца находится число  . В общем виде матрицу
. В общем виде матрицу  .
. , т.е. число строк и число столбцов матрицы совпадают, то такая матрица называется квадратной порядка
, т.е. число строк и число столбцов матрицы совпадают, то такая матрица называется квадратной порядка 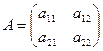
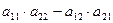 , составленное из элементов матрицы
, составленное из элементов матрицы  .
. . (1)
. (1) ).
). . (2)
. (2) и диагональ, образованную числами
и диагональ, образованную числами  , которую будем называть побочной. Вычисляем произведение элементов, стоящих на главной диагонали и два произведения чисел, расположенных в вершинах двух равнобедренных треугольников с основаниями, параллельными главной диагонали. Складываем эти три произведения. Из полученной суммы вычитаем сумму произведений элементов, стоящих на побочной диагонали и двух произведений чисел, расположенных в вершинах двух равнобедренных треугольников с основаниями, параллельными побочной диагонали.
, которую будем называть побочной. Вычисляем произведение элементов, стоящих на главной диагонали и два произведения чисел, расположенных в вершинах двух равнобедренных треугольников с основаниями, параллельными главной диагонали. Складываем эти три произведения. Из полученной суммы вычитаем сумму произведений элементов, стоящих на побочной диагонали и двух произведений чисел, расположенных в вершинах двух равнобедренных треугольников с основаниями, параллельными побочной диагонали. Рисунок 1
Рисунок 1
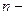 го порядка
го порядка  .
. .
. любого элемента
любого элемента 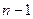 , получающийся из определителя
, получающийся из определителя  , для определителя
, для определителя  . (3)
. (3) можно вычислять по формуле (3), которая представляет собой разложение определителя
можно вычислять по формуле (3), которая представляет собой разложение определителя  . (4)
. (4) .
. .
. .
. .
. .
. ;
; ;
; или
или  ;
; или
или  .
.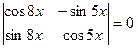 .
. .
. .
. ;
; ;
; .
. .
. .
.
 .
. .
. .
. .
. .
. .
. ;
; ;
; .
. .
. .
.
 элементов
элементов  . Эти определители можно вычислить либо по формуле (2), как это сделано выше, либо по правилам (3), (4).
. Эти определители можно вычислить либо по формуле (2), как это сделано выше, либо по правилам (3), (4). плоскости в данной системе координат однозначно характеризуется двумя числами
плоскости в данной системе координат однозначно характеризуется двумя числами  , которые называются координатами точки
, которые называются координатами точки  , начало которого (точка O) совпадает с началом координат, а конец находится в точке
, начало которого (точка O) совпадает с началом координат, а конец находится в точке 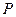 трёхмерного пространства в заданной прямоугольной декартовой системе координат соответствует упорядоченная тройка чисел
трёхмерного пространства в заданной прямоугольной декартовой системе координат соответствует упорядоченная тройка чисел 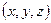 , называемых координатами точки
, называемых координатами точки  в прямоугольной декартовой системе координат в трёхмерном пространстве.
в прямоугольной декартовой системе координат в трёхмерном пространстве. называют направленный отрезок прямой; при этом отрезок прямой линии называется направленным отрезком, если указано, какой из его концов считается началом отрезка, а какой – концом.
называют направленный отрезок прямой; при этом отрезок прямой линии называется направленным отрезком, если указано, какой из его концов считается началом отрезка, а какой – концом. называют число
называют число  , равное
, равное . (5)
. (5)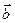 называются равными
называются равными  , если они коллинеарны, имеют одинаковую длину и сонаправлены, т.е. если
, если они коллинеарны, имеют одинаковую длину и сонаправлены, т.е. если 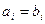 для всех значений индекса
для всех значений индекса  .
. определяется равенством
определяется равенством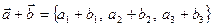 .
.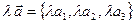 .
. называются линейно независимыми, если равенство нулю их линейной комбинации
называются линейно независимыми, если равенство нулю их линейной комбинации  возможно лишь в случае, когда все числа
возможно лишь в случае, когда все числа  равны нулю.
равны нулю. образуют в пространстве базис, если любой вектор
образуют в пространстве базис, если любой вектор  этого пространства может быть представлен в виде некоторой линейной комбинации векторов
этого пространства может быть представлен в виде некоторой линейной комбинации векторов  .
.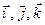 . Каждый из этих векторов имеет длину, равную единице и любые два из них перпендикулярны. Направления векторов
. Каждый из этих векторов имеет длину, равную единице и любые два из них перпендикулярны. Направления векторов  совпадают с направлениями декартовых осей
совпадают с направлениями декартовых осей 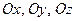 соответственно.
соответственно.
 равны
равны  .
.