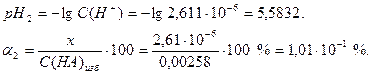|
|
Расчет концентрации ионов водорода и гидроксид-ионов в буферных растворахБуферными растворами называют такие растворы, рН которых остается приблизительно постоянным при добавлении небольших количеств сильной кислоты или щелочи. Буферными свойствами обладают растворы, образованные: - слабой кислотой и ее солью; - слабым основанием и его солью; - средней и кислой солями; - двумя кислыми солями. Во всех этих случаях при добавлении сильной кислоты или щелочи происходит смещение равновесия диссоциации соответствующего слабого электролита (кислоты или основания), в результате чего рН раствора почти не изменяется. Рассмотрим буферный раствор, образованный слабой уксусной кислотой и ее солью ацетатом натрия (ацетатный буферный раствор). Запишем реакции диссоциации этих веществ: Cк – х х х CH3COOH ↔ CH3COO– + H+ Сс Сс Сс CH3COONa → CH3COO– + Na+ Обозначим начальную концентрацию кислоты Ск. Если продиссоциировало х моль/л кислоты, то осталось (Ск – х) CH3COOH и образовалось х моль/л CH3COO– и х моль/л H+. Если начальная концентрация соли Cс, то в результате ее полной диссоциации образуется столько же ионов CH3COO– и Na+. Запишем выражение константы диссоциации уксусной кислоты:
Выразим х:
Обычно, х<<Сс и х<<Ск, тогда (х + Сс) ≈ Сс, а (Ск– х) ≈ Ск. Тогда уравнение (22) примет следующий вид:
Задача 7 К V1 (мл) C1 молярного раствора одноосновной кислоты НА с константой диссоциации К добавили V2 (мл) Сн2 нормального раствора щелочи (таблица 13). Рассчитайте рН и степень диссоциации в исходном (1) и в полученном (2) растворах. Объясните изменение степени диссоциации кислоты. Таблица 13 – Условие задачи 7
Разберем решение задачи на примере 1 варианта. Рассчитаем рН и степень диссоциации в растворе чистой одноосновной кислоты (раствор 1). Запишем реакцию диссоциации кислоты: 0,044–х х х HA ↔ H+ + A–
Пусть продиссоциировало х моль/л кислоты НА, тогда осталось в (С0 – х) или (0,044 – х) и образовалось х моль/л ионов Н+ и х моль/л ионов А–. Подставим эти обозначения в константу диссоциации кислоты:
Решим это уравнение исходя из предположения, что х<<С0 (20), тогда:
Степень диссоциации кислоты больше 0,1 %. Поэтому этот расчет необходимо повторить с использованием точного уравнения (18):
Рассчитаем рН раствора и степень диссоциации кислоты:
Запишем уравнение реакции, протекающей в растворе 2: HA + NaOH → NaA + H2O HA + Na+ + OH– → Na+ + A– + H2O HA + OH– → A– + H2O. Рассчитаем количества щелочи и кислоты, которые были взяты для реакции. Фактор эквивалентности NaOH равен 1, и его нормальная концентрация равна молярной концентрации: n(NaOH) = 0,04 ∙ 0,036 = 0,001400 (моль); n(HA) = 0,044 ∙ 0,037 = 0,001628 (моль). Кислота взята в избытке, который равен: n(HA)изб = 0,001628 – 0,001400 = 0,0001880 (моль). В результате реакции образовалась соль, количество которой будет равно количеству щелочи (n(NaA) = n(NaOH) = 0,001400 моль). В растворе протекают следующие реакции: HA ↔ H+ + A– NaA → Na+ + A– Рассчитаем концентрации веществ, находящихся в растворе. Общий объем раствора равен: Vобщ = 36 + 37 = 73 мл или 0,073 л.
Для расчета рН буферного раствора используем уравнение (23):
По сравнению с исходным раствором НА степень диссоциации значительно уменьшилась (с 2,11 до 0,101 %), несмотря на то, что концентрация кислоты также уменьшается с 0,044 моль/л до 0,002575 моль/л (уменьшение концентрации, как известно, должно приводить к увеличению степени диссоциации). Это можно объяснить тем, что при добавлении щелочи в раствор кислоты образуется большой избыток ионов А–, которые смещают равновесие диссоциации НА влево и уменьшают степень диссоциации. Таблица 14 – Ответы к задаче 7

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 (21)
(21) (22)
(22) (23)
(23)
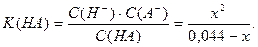

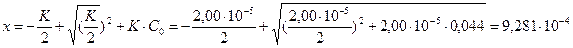 (моль/л).
(моль/л).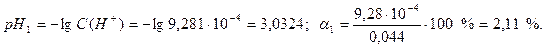
 (моль/л).
(моль/л). (моль/л).
(моль/л). (моль/л).
(моль/л).