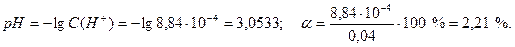|
|
Равновесия в растворах электролитовРасчет концентрации ионов водорода и рН в растворах сильных кислот И оснований При растворении вещества в воде могут образовываться ионы. Частичный или полный распад вещества на ионы в результате взаимодействия с растворителем называют электролитической диссоциацией. Одной из основных характеристик электролитической диссоциации является степень диссоциации (α), которая равна отношению концентрации продиссоциировавших молекул к начальной концентрации растворенного вещества. Степень диссоциации зависит от: природы растворителя; природы растворенного вещества; концентрации раствора (чем меньше концентрация раствора, тем больше степень диссоциации); температуры; наличия одноименного иона. По степени диссоциации все электролиты делятся на сильные и слабые. Сильные электролиты в не слишком концентрированных растворах практически полностью диссоциируют на ионы. К сильным электролитам относятся: - все растворимые в воде основания (LiOH, NaOH, KOH, RbOH, CsOH, Ca(OH)2, Sr(OH)2, Ba(OH)2, Ra(OH)2; - сильные кислоты (HNO3, H2SO4, HCl, HBr, HI, HClO4 и некоторые другие); - почти все растворимые в воде соли, в том числе и комплексные. Задача 5 В мерную колбу объемом V1 (мл) внесли V2 (мл) раствора S1 с концентрацией C1 (моль/л) (таблица 9). Объем раствора довели до метки. Какова молярная и нормальная концентрации полученного раствора и его рН? Таблица 9 – Условие задачи 5
Продолжение таблицы 9
Разберем решение этой задачи на примере вариантов 1 и 2. Рассчитаем концентрацию раствора серной кислоты С2 (вариант 1), полученную при разбавлении раствора С1. Воспользуемся законом разбавления (14):
Найдем нормальную концентрацию раствора (7):
Запишем уравнение диссоциации серной кислоты. Это сильный электролит, который нацело диссоциирует на ионы: 0,0010 2∙0,0010 H2SO4 → 2H+ + SO42– Если начальная концентрация H2SO4 равна 0,00100 моль/л, то, согласно уравнению реакции, концентрация образовавшихся ионов водорода в два раза больше и равна 0,00200 моль/л. Рассчитаем рН полученного раствора: рН = –lg C(H+) = –lg 0,00200 = 2,6990 (рН = 2,70). Полученный результат можно округлить с точностью до ±0,01 рН, в соответствии с точностью обычного рН-метра. Аналогично решаем эту задачу для второго варианта. Рассчитываем концентрацию раствора Ba(OH)2, полученного после разбавления раствора С1 и его нормальность Сн:
Запишем диссоциацию гидроксида бария: 0,0224 2·0,0224 Ba(OH)2 → Ba2+ + 2OH– С(ОН–) = 0,04480 моль/л. Рассчитаем рН раствора: рОН = –lg C(OH–) = –lg 0,04480 = 1,3487; рН = 14 – рОН = 14 – 1,3487 = 12,6513 (рН = 12,65). Таблица 10 – Ответы к задаче 5
Расчет концентрации ионов водорода и рН в растворах слабых кислот И оснований Слабые электролиты диссоциируют не полностью, в их растворах кроме ионов присутствуют также и недиссоциированные молекулы, концентрации которых связаны константой диссоциации. Например, для слабой кислоты HA константа диссоциации может быть записана следующим образом: С0–х х х HA ↔ H+ + A–
Если начальную концентрацию кислоты принять равной С0, а концентрацию продиссоциировавшей кислоты считать равной х, тогда в результате протекания реакции диссоциации в растворе останется (С0 – х) моль/л молекул кислоты и образуется х моль/л ионов водорода (С(Н+) = х) и х моль/л анионов кислоты (С(А–) = х). Эти концентрации для участников реакции называются равновесными. Для определения равновесных концентраций необходимо решить следующее квадратное уравнение:
Степень диссоциации НА (α) равна:
Если степень диссоциации слабой кислоты мала (меньше 0,1 %), то х<<С0 и в знаменателе уравнения (17) можно пренебречь величиной х:
В случае, когда в растворе находится слабое основание, например гидроксид аммония NH4OH, в растворе в равновесии будут находиться его молекулы (C0 – х), гидроксид-ионы ОН– (х) и ионы аммония NH4+ (х). Диссоциацию этого вещества в водном растворе и соответствующую константу диссоциации можно представить следующим образом: С0–х х х NH4OH ↔ NH4+ + OH–
Решая это уравнение, можно найти х, который в этом случае будет равен концентрации ионов ОН–. Поэтому сначала будет получена величина рОН, а затем рН. Задача 6 Рассчитайте рН и степень диссоциации слабой одноосновной кислоты, если ее константа диссоциации равна К, а концентрация раствора – С0 (моль/л) (таблица 11). Таблица 11 – Условие задачи 6
Пример решения задачи 6 (вариант 1). Запишем уравнение электролитической диссоциации слабой одноосновной кислоты НА: 0,040–х х х HA ↔ H+ + A–
Пусть продиссоциировало х моль/л кислоты НА, тогда осталось в (С0 – х) или (0,040 – х) и образовалось х моль/л ионов Н+ и х моль/л ионов А–. Подставим эти обозначения в константу диссоциации кислоты:
Сначала проверим возможность упрощенного решения квадратного уравнения. Для этого решим это уравнение исходя из предположения, что х<<С0 (20), тогда:
Степень диссоциации этой кислоты достаточно мала, однако значение 2,24 % превышает желаемую аналитическую точность определения 0,1 %. Поэтому этот расчет необходимо повторить с использованием точного уравнения (18):
Рассчитаем рН раствора и степень диссоциации кислоты:
Таблица 12 – Ответы к задаче 6 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 (моль/л).
(моль/л). (моль экв/л).
(моль экв/л).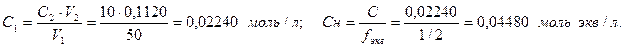
 (моль/л). (16)
(моль/л). (16)
 (19)
(19) (20)
(20)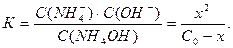

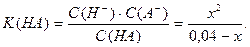
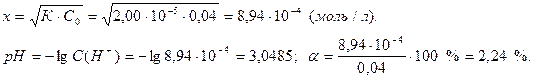
 (моль/л).
(моль/л).