
|
|
Обратная форма закона ГукаЛекция 5. Закон Гука для изотропного материала Постановка задачи Все известных нам в природе материалы элементов конструкций деформируются под действием приложенных к ним сил. В расчетах материалы отличаются на упругие и пластичные. Процесс деформирования в каждом элементе , приложенные силы, производят некоторую работу. Если материал упругий, то эта работа запасается в виде потенциальной энергии, которая освобождается по мере того, как уменьшаются деформирующие силы. Если материал пластичный, то работа, произведенная приложенными к нему внешними силами, пойдет на изменение его физического состояния или вызовет нагревание. Чем больше жесткость материала, тем меньше при данной системе приложенных сил запасенная работа. Две формы обобщенного закона Гука Прямая форма закона Гука При одноосном растяжении стержня, вызванном действием внешних сил (рис. 5.1, а), в каждой частице этого стержня возникают положительные продольные ε1 и отрицательные поперечные (ε2 и ε3) главные деформации, которые связаны между собой зависимостью
где ν — коэффициент Пуассона. Верхние индексы здесь совпадают с обозначением оси 1, по направлению которой действует напряжения σ1. Используя закона Гука где Е — модуль Юнга.
Рис. 5.1. Одно и трехосное напряженное состояние В случае трехосного растяжения частица упругого тела подвержена одновременному действию трех главных напряжений (рис. 5.1, б). От действия напряжений по оси 2 в частице появятся деформации, которым, по аналогии с (5.2), присвоим верхний индекс, совпадающий с индексом напряжения σ2:
От напряжений σ3 получим деформации, которые сопроводим индексом 3:
Полная деформация частицы в направлении главной оси 1, в соответствии с принципом независимости сил, выразится суммой:
Похожие трехчленные выражения будут и для полных деформаций ε2 и ε3. В результате получим формулы обобщенного закона Гука в прямой форме, выражающие деформации через напряжения:
Из формул (5.3) следует вывод, что деформации изотропного тела могут быть представлены только двумя упругими константами материала(модулем Ε и коэффициентом Пуассона ν) и их вполне достаточно. Сложив, левые и правые части выражений (5.3), после упрощений получим закон Гука для объемной деформации
где Отсюда, в частности, следует вывод о том, что для изотропного материала коэффициент Пуассона не может быть больше 0,5. Действительно, в случае всестороннего сжатия материала напряжением σ, например, сумма главных напряжений Σ = – 3 σ и, согласно (5.4), имеем:
То есть объемная деформация будет отрицательной только в том случае, если коэффициент В природе пока не обнаружено изотропных материалов с коэффициентом
обратная форма закона Гука Перепишем первое из трех выражений (5.3) в следующем виде:
Отсюда найдем
и, с учетом (5.4), получим
Введем обозначения для множителей при деформациях
В результате имеем:
В отличие от выражений (5.3), формулы (5.7) вместо упругих констант Е и ν содержат две другие постоянные, λ и μ, которые называются упругими постоянными Ламе14 (константами Ламе). Из формул (5.6) можно получить и обратные зависимости, т. е. выразить Е и ν через постоянные Ламе:
Сложив, левые и правые части выражений (5.7), получим обратную форму записи закона Гука для объемной деформации:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 (5.1)
(5.1) выразим относительные деформации ɛ в (5.1) через заданное напряжение σ1:
выразим относительные деформации ɛ в (5.1) через заданное напряжение σ1:  ,
, 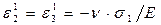 , (5.2)
, (5.2)
 ,
,  , (c)
, (c) ,
, 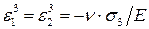 , (d)
, (d)
 .
. (5.3)
(5.3) , (5.4)
, (5.4)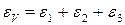 — объемная относительная деформация,
— объемная относительная деформация, 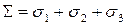 — сумма главных напряжений. В такой форме закон Гукаутверждает, что объемная деформация пропорциональна сумме трех главных напряжений.
— сумма главных напряжений. В такой форме закон Гукаутверждает, что объемная деформация пропорциональна сумме трех главных напряжений.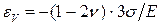 . (5.5)
. (5.5) , в противном случае деформация
, в противном случае деформация  будет положительной и тело при сжатии не уменьшится, а увеличится в объеме, что противоестественно.
будет положительной и тело при сжатии не уменьшится, а увеличится в объеме, что противоестественно. . Однако есть много материалов с коэффициентом Пуассона близким к значению 0,5 (например, резина, парафин и др.). Для пластической стали в состоянии текучести значение коэффициента ν также близко к 0,5. Поэтому, для упрощения математических выкладок, в прикладных задачах величине ν часто придают значение 0,5. В таких случаях
. Однако есть много материалов с коэффициентом Пуассона близким к значению 0,5 (например, резина, парафин и др.). Для пластической стали в состоянии текучести значение коэффициента ν также близко к 0,5. Поэтому, для упрощения математических выкладок, в прикладных задачах величине ν часто придают значение 0,5. В таких случаях  и объем тела не изменяется; материал как бы наделяется свойством несжимаемости. Таким образом, если та или иная проблема решается в предположении о несжимаемости материала, это означает, что в выкладках принято значение
и объем тела не изменяется; материал как бы наделяется свойством несжимаемости. Таким образом, если та или иная проблема решается в предположении о несжимаемости материала, это означает, что в выкладках принято значение 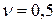 .
.
 или
или  .
.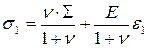
 .
. и
и 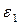
 ,
,  . (5.6)
. (5.6) . Выполнив аналогичные преобразования со второй и третьей формулами (5.6), получим обобщенный закон Гука в обратной форме, в котором напряжения выражаются через деформации:
. Выполнив аналогичные преобразования со второй и третьей формулами (5.6), получим обобщенный закон Гука в обратной форме, в котором напряжения выражаются через деформации: . (5.7)
. (5.7) ,
,  . (5.8)
. (5.8) . (5.9)
. (5.9)