
|
|
На основании (10), подобно (7), получаемСущность модального управления и его преимущества. Суть модального управления состоит в определении численных значений коэффициентов передачи безынерционных ОС по всем переменным состояния объекта с целью обеспечения заданного распределения корней характеристического уравнения замкнутой САУ. Корни характеристического уравнения САУ полностью определяют ее свободное движение
Каждая составляющая В технической литературе приводятся различные наборы стандартных характеристических полиномов 1-8 порядков и соответствующие им графики переходных процессов с указанными на них показателями качества (биноминальные полиномы Ньютона, полиномы Баттерворта и др.). Исходя из порядка объекта и заданных в техническом задании показателей качества САУ, проектант может выбрать требуемый график переходного процесса и соответствующий ему «стандартный» характеристический полином, а затем, используя излагаемый далее алгоритм, выполнить синтез модальных ОС, обеспечивающих заданные показатели качества САУ. Таким образом, теория модального управления позволяет осуществлять синтез многоконтурных замкнутых САУ с заранее заданными показателями качества. Отсюда следуют четыре наиважнейших достоинства модального управления: 1. Синтезированная модальная САУ не требует проверки на устойчивость (так как она заранее должна быть устойчивой и обладать требуемой степенью устойчивости). 2. Синтезированная модальная САУ не требует введения дополнительных корректирующих устройств (так как она сама уже удовлетворяет требуемым показателям качества). 3. Введение модальных ОС, в силу их безынерционности, не повышает порядок объекта и не нарушает его управляемость и наблюдаемость (что зачас- тую происходит при введении пассивных инерционных корректирующих устройств).
4. Относительная простота и экономичность технической реализации модальных САУ (так как реализации модальных ОС может быть выполнена с помощью маломощных измерительно-преобразовательных устройств и электронных усилителей с малыми тепловыми потерями).
Синтез одномерных модальных регуляторов. Постановка задачи. Задано уравнение полностью управляемого объекта с одним входом:
где Требуется определить коэффициенты передачи
при которых замкнутая САУ имела бы желаемый «стандартный» характеристический полином
Решение задачи базируется на использовании следующей теоремы: пусть матрицы полностью управляемой системы представлены в двух различных базисах
где
На основании (1), (2) запишем уравнение свободного движения замкнутой САУ
Определяем характеристический полином матрицы A:
Записываем соответствующую ему пару
(такая форма записи называется нормальной формой).
Теперь согласно (6), (5), (4) можно вычислить матрицу канонического преобразования P и записать уравнение объекта (1) в канонической форме
где
при этом, естественно, матрицы На основании (10), подобно (7), получаем
Для полинома (3), подобно (9), можно записать
Из (12), (13) очевидно, что
Поскольку
то согласно (14), с учетом (9), (13), получаем
Отсюда
или
Таким образом, коэффициенты передачи модального регулятора (модальных ОС) в каноническом виде определяются как разность соответствующих коэффициентов желаемого «стандартного» характеристического полинома САУ (3) и характеристического полинома объекта (8). Используя (11), находим искомую матрицу-строку коэффициентов передачи модального регулятора в исходном базисе: kт= Для проверки полученного решения задачи целесообразно, согласно (7), (16), вычислить матрицу
и определить ее характеристический полином
Совпадение коэффициентов этого полинома с соответствующими коэффициентами желаемого полинома (3) указывает на правильность решения задачи. Исходя из изложенного, можно предложить следующий алгоритм синтеза одномерных модальных регуляторов. Шаг 1. На основании (1) определяется характеристический полином a(p) матрицы A вида (8). Шаг 2. Выбирается желаемый “стандартный” характеристический полином g(p) вида (3). Шаг 3. Согласно (15) вычисляются коэффициенты передачи регулятора в каноническом базисе, которые записываются в виде вектор-строки Шаг 4. На основании (1), (5) составляется матрица управляемости Rв исходном базисе. Шаг 5. Для полинома a(p) составляется каноническая пара Шаг 6. На основании (9), (6) составляется матрица управляемости Шаг 7. Согласно (4) вычисляется матрица преобразования P. Шаг 8. Согласно (16) вычисляется вектор-строка коэффициентов передачи регулятора в исходном базисе kт. Указанный алгоритм легко реализуется для вычислений на ЦВМ на базе стандартных программ матричной алгебры. Пример 1. Заданы структурная схема и параметры объекта (рис. 1).
        xвх + u xвх + u  x2 x2  x1 x1
  
Рис. 1 Корни характеристического уравнения данного объекта p1= -1/T1 = -2; p2 = -1/T2= -1, следовательно, степень его устойчивости η = 1. Требуется определить коэффициенты обратных модальных связей
желаемые значения корней p1 = p2 = -3 и соответствующую им степень устойчивости η = 3 замкнутой системы. На основании рис. 1 запишем
Отсюда
при этом матрицы Aиbуравнения (1) имеют вид A = Дальнейший синтез модального регулятора выполняем в строгом соответствии с приведенным выше алгоритмом:
1) a(p) = 2) g(p) = (p - p1)(p - p2) = (p + 3)(p + 3) =p2 + 6p + 9; 3) 4) 5) 6) 7)
8) Проверка. Согласно (17) вычисляем
Полученный характеристический полином замкнутой модальной системы совпадает с указанным ранее желаемым полиномом g(p), следовательно, коэффициенты Безынерционные модальные ОС изменяют общий коэффициент передачи системы и тем самым влияют на установившееся значение выходной переменной объекта. Чтобы исключить такое влияние, достаточно на входе системы (рис. 1) установить безынерционный усилитель, коэффициент усиления ky которого определяется из равенства коэффициента усиления kм замкнутой модальной САУ и коэффициента усиления k0самого объекта:
Пусть теперь модель объекта представлена в форме его передаточной функции вида
которой соответствует матричное уравнение состояния
Здесь матрицы A и b уже имеют нормальную форму (9), т.е. A=
поэтому согласно (5), (6)
Первое из равенств (20) означает, что в данном случае коэффициенты передачи модального регулятора сразу же могут быть вычислены по формулам (15). Равенство же (21) означает, что на выходе такого регулятора последовательно с ним должен быть включен общий для всех каналов регулятора усилитель с коэффициентом усиления равным величине Подставив (21) в (19), получаем
Это уравнение совпадает с уравнением (7), поэтому для проверки решения подобно (17), следует вычислить матрицу G’= A - bkT и определить ее характеристический полином. Пример 2.Пусть как и в предыдущем примере объект представляет собой апериодическое звено второго порядка (рис. 2) с теми же значениями параметров. Отличие же состоит в том, что теперь доступной для управления является только одна выходная переменная объекта x1.
     + u + u 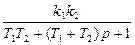 x1 x1
     k1 = 1; T1 = 0.5; k2 = 2; T2 =1 k1 = 1; T1 = 0.5; k2 = 2; T2 =1
  + +
Рис. 2 Требуется определить коэффициенты g(p) = p2+ g1p + g0 = p2 + 6p + 9
Тогда на основании (21), (20), (15) находим искомые коэффициенты k=1/b0=1/4;
Таким образом, при тех же параметрах объекта, но измеряемой только одной из его переменных получили увеличенные, по сравнению с примером 1, значения коэффициентов модальных ОС. Проверка. На основании (23) записываем матрицы объекта в нормальной форме
Далее согласно (17) вычисляем
и тогда
Полученный полином совпадает с ранее принятым “стандартным” характеристическим полиномом g(p), следовательно, коэффициенты Для определения коэффициента усилителя ky запишем коэффициент передачи всей системы рис. 2 и приравняем его к коэффициенту передачи самого объекта:
т.е. получили то же значение, как и в примере 1, что дополнительно подтверждает правильность вычисленных коэффициентов
Л и т е р а т у р а: 1. Кузовков Н. Т. Модальное управление и наблюдающие устройства. М.: Машиностроение, 1976. 2. Кухаренко Н. В. Синтез модальных регуляторов при неполной управляемости объектов // Техническая кибернетика, 1992, № 3, с. 3-10. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


 такого движения, соответствующая отдельному корню pi (или паре комплексно сопряженных корней), в зарубежной литературе называется модой – отсюда и термин «модальное управление». Корни уравнения однозначно зависят от его коэффициентов, поэтому модальное управление можно трактовать как целенаправленное изменение коэффициентов характеристического уравнения объекта с помощью безынерционных ОС.
такого движения, соответствующая отдельному корню pi (или паре комплексно сопряженных корней), в зарубежной литературе называется модой – отсюда и термин «модальное управление». Корни уравнения однозначно зависят от его коэффициентов, поэтому модальное управление можно трактовать как целенаправленное изменение коэффициентов характеристического уравнения объекта с помощью безынерционных ОС. , (1)
, (1)
 - вещественные матрицы указанных размерностей.
- вещественные матрицы указанных размерностей. модального регулятора
модального регулятора , (2)
, (2) (3)
(3) и
и  . Тогда матрица преобразования P пары
. Тогда матрица преобразования P пары  (4)
(4) ; (5)
; (5)  (6)
(6) (7)
(7) (8)
(8) =
=  ;
;  =
=  ; (9)
; (9) ,
,  , (10)
, (10) = P A P-1;
= P A P-1;  = P b;
= P b;  = PX
= PX  X = P-1
X = P-1 ;
; =kTP-1; (11)
=kTP-1; (11) будут иметь нормальную форму (9).
будут иметь нормальную форму (9). (12)
(12) =
= 
 =
=  ,
, =
=  ;
;  ; … ;
; … ;  ;
; 
 ,
,  (15)
(15) P (16)
P (16) =A - bkT (17)
=A - bkT (17)
 .
. вида (9).
вида (9). в каноническом базисе.
в каноническом базисе.




 k1=1; T1=0.5; k2=2; T2=1
k1=1; T1=0.5; k2=2; T2=1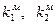 , обеспечивающих
, обеспечивающих

 ;
; ,
, =
=  ; b =
; b = 

 = p2 +3p+2;
= p2 +3p+2; ;
;  ;
;  ;
; ;
;  ;
; ;
;  ;
; ;
; ;
; 
 ;
; 
 ;
; 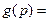

 определены правильно.
определены правильно.

 (18)
(18)
 или в более компактной форме
или в более компактной форме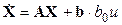 (19)
(19) ,
,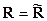 , а согласно (4)
, а согласно (4) 
 . Тогда на основании (11), (10) имеем
. Тогда на основании (11), (10) имеем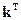 ;
;  ;
;  (20)
(20) (21)
(21) (это равноценно уменьшению всех расчетных коэффициентов регулятора в
(это равноценно уменьшению всех расчетных коэффициентов регулятора в  раз).
раз). (22)
(22)



 -
- k
k 
 +
+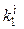
 при которых “стандартный” характеристический полином модальной САУ имел бы ранее принятый вид
при которых “стандартный” характеристический полином модальной САУ имел бы ранее принятый вид (23)
(23) =>
=> 
 ;
; 


 определены правильно.
определены правильно.

 ,
, .
. 