
|
|
Основное уравнение молекулярно-кинетической теории
В молекулярно-кинетической теории (МКТ) элементарным объектом является молекула – мельчайшая частица вещества, определяющая его физико-химические свойства. Основные положения этой теории заключаются в том, что – вещество состоит из мельчайших частиц – молекул; – все молекулы находятся в постоянном беспорядочном тепловом движении, при котором они обмениваются импульсами и энергией.
Молекулярно – кинетическая теория позволяет получить обоснование термодинамических законов и более глубоко объяснить их физическую сущность.
С молекулярной точки зрения идеальным называют газ, удовлетворяющий следующим условиям: – объём самих молекул данного количества газа пренебрежимо мал по сравнению с объёмом сосуда, в котором находится это количество газа; – время столкновения молекул газа друг с другом пренебрежимо мало по сравнению со временем между двумя столкновениями (т.е. временем свободного пробега молекулы); – молекулы взаимодействуют между собой только при непосредственном соприкосновении, при этом они отталкиваются; – силы притяжения между молекулами идеального газа ничтожно малы, и ими можно пренебречь. Микроскопическими параметрами газа называют индивидуальные характеристики молекул, таких как скорость, импульс и кинетическая энергия поступательного движения. Одной из важнейших задач МКТ было установление связи между микроскопическими параметрами газа и макроскопическими параметрами (р, V, T, ν).
Используя модель идеального газа, вычислим давление газа на стенку сосуда.
Предположим, что в сосуде находится одно вещество, т.е. все молекулы имеют одинаковую массу т0и обладают скоростями, различными по направлению, но одинаковыми по модулю. Выберем на стенке сосуда малый участок, площадью ΔS. Так как стенки сосуда, в котором заключён газ, подвергаются непрерывной бомбардировке молекулами, то элементу стенки ΔS сообщается за секунду некоторый импульс, который равен силе, действующей на ΔS. Удар молекулы о стенку будем считать упругим, т.е. υпад = υотр .Тогда изменение импульса молекулы Δ(т0.υх) = – 2т0.υх. За время Δt к стенке подлетят все молекулы, расположенные в цилиндре с основанием ΔS и образующей l = υx.Δt. Число этих молекул
Изменение их импульса равно:
Таким образом сила, действующая на участок ΔS в соответствии с основным уравнением динамики равна:
Давление на стенку сосуда Так как все направления для векторов скоростей молекул равновероятны, то средние значения квадратов модулей их проекций на координатные оси равны между собой:
Учитывая, что на самом деле, молекулы движутся с разными скоростями, необходимо вместо квадрата скорости поставить среднее значение квадрата скорости всех молекул:
Окончательно получаем уравнение Клаузиуса или основное уравнение МКТ:
Выразив плотность вещества через т0и п
получим ещё одно выражение для основного уравнение МКТ
Величина
называют средней квадратичной скоростьюмолекул. Сравнивая основное уравнение МКТ с уравнением состояния идеального газа
p = n.k.T,
получаем Таким образом, можно утверждать, что температура макросистемы хоть и измеряется с помощью макроскопического прибора – термометра и является макроскопическим параметром, она имеет в МКТ смысл микроскопического параметра, а, именно, термодинамическая температура является величиной прямо пропорциональной кинетической энергии теплового движения молекул. В молекулярной физике энергию теплового движения можно выражать и в кельвинах и в джоулях: 1 К = 1,38 . 10–23 Дж 1 Дж = 7,246 . 1022 К.
Наряду с поступательным движением возможно также вращение молекулы и колебания атомов, входящих в состав молекулы. Числом степеней свободыназывают число независимых координат, определяющих положение системы (в нашем случае – молекулы). Для определения положения центра масс молекулы необходимо задать три координаты. Это означает, что молекула имеет три поступательных степени свободы.
Такимобразом, жёсткая двухатомная молекула имеет пять степеней свободы. Если молекула упругая, то возможны колебания атомов и необходима ещё одна степень свободы (расстояние между атомами) – колебательная степень свободы. Так как средняя энергия поступательного движения молекулы равна Для полной средней энергии молекулы имеем:
Число i совпадает с числом степеней свободы только для жёстких молекул. Молекулы идеального газа не взаимодействуют между собой. Поэтому внутреннюю энергию некоторого количества идеального газа можно найти как сумму средних энергий всех молекул газа:
Длиной свободного пробега молекулы газа λ называют среднее расстояние, которое пролетает молекула между очередными её столкновениями с другими молекулами газа.
Таким образом, на одну молекулу газа в среднем приходится объём
Так как концентрацию п молекул газа можно представить в виде
Если в лабораторной системе отсчёта средняя скорость молекул равна
Если υ1и υ2 –скорости молекул 1 и 2, а φ –угол между направлениями векторов этих скоростей то
Так как скорости молекул могут иметь любые произвольные направления, а их средние значения в равновесном газе одинаковые, то усреднение последнего соотношения по всем возможным углам φдаёт
Считая, что средние квадраты скоростей молекул пропорциональны квадратам их средних скоростей, получаем
Выражение для длины свободного пробега принимает вид
Средняя частота соударений молекулы газа с другими молекулами

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 Пусть в сосуде находится идеальный газ с концентрацией молекул
Пусть в сосуде находится идеальный газ с концентрацией молекул 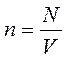 , где N – общее число молекул, V – объём сосуда.
, где N – общее число молекул, V – объём сосуда. .
. .
. .
. .
. т.е.
т.е.  и
и .
. .
. .
.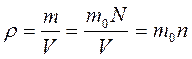 ,
, .
.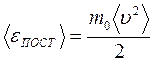 есть средняя кинетическая энергияпоступательного движения молекул , а величину
есть средняя кинетическая энергияпоступательного движения молекул , а величину
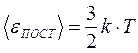 и
и  .
. Если молекула двухатомная и жёсткая («гантель»), то, кроме трёх поступательных степеней свободы, она имеет и две вращательные степени свободы, связанные с углами поворота вокруг двух взаимно перпендикулярных осей 1–1 и 2–2, проходящих через центр масс С .
Если молекула двухатомная и жёсткая («гантель»), то, кроме трёх поступательных степеней свободы, она имеет и две вращательные степени свободы, связанные с углами поворота вокруг двух взаимно перпендикулярных осей 1–1 и 2–2, проходящих через центр масс С . , то получается, что на каждую степень свободы в среднем приходится энергия
, то получается, что на каждую степень свободы в среднем приходится энергия  . На колебательную степень свободы должны приходиться в среднем по две половинки
. На колебательную степень свободы должны приходиться в среднем по две половинки  – одна в виде кинетической и одна в виде потенциальной.
– одна в виде кинетической и одна в виде потенциальной. , где
, где i =zпост + zвр +2zкол .
i =zпост + zвр +2zкол .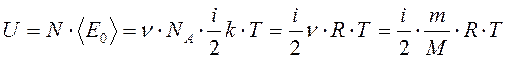 .
. Для оценки λбудем считать, что молекулы идеального газа представляют собой твёрдые шары диаметром d , которые взаимодействуют между собой только путём упругих соударений при непосредственном соприкосновении. При рассмотрении взаимодействия двух молекул систему отсчёта свяжем с центром молекулы 1. В этой системе отсчёта молекула 2 движется со скоростью
Для оценки λбудем считать, что молекулы идеального газа представляют собой твёрдые шары диаметром d , которые взаимодействуют между собой только путём упругих соударений при непосредственном соприкосновении. При рассмотрении взаимодействия двух молекул систему отсчёта свяжем с центром молекулы 1. В этой системе отсчёта молекула 2 движется со скоростью 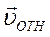 и проходит расстояние L c момента предыдущего столкновения с молекулой 1. Молекула 2 не испытает ни одного столкновения с другими молекулами, если не будет ни одного их центра внутри цилиндра с площадью основания πR2 = πd2 и длиной L.
и проходит расстояние L c момента предыдущего столкновения с молекулой 1. Молекула 2 не испытает ни одного столкновения с другими молекулами, если не будет ни одного их центра внутри цилиндра с площадью основания πR2 = πd2 и длиной L. .
. , то
, то  .
. , а средняя относительная скорость молекулы 2 в системе отсчёта, связанной с молекулой 1 равна
, а средняя относительная скорость молекулы 2 в системе отсчёта, связанной с молекулой 1 равна 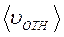 , то длина свободного пробега λи расстояние L будут связаны соотношением
, то длина свободного пробега λи расстояние L будут связаны соотношением .
.
 .
. .
.
 .
. , где
, где – эффективное сечение взаимодействия.
– эффективное сечение взаимодействия. .
.