|
|
Признаки истинности простого сообщения.Рассматриваемое простое сообщение имеет числовые компоненты 4, 2, 6. Как видно, один из них больше каждого из двух других. Данное число называется наибольшим число простого сообщения, 6 – наибольшее число. Главный опорный термин простого сообщения относится к наибольшему числу этого сообщения. Наибольшее число представляет собой значение суммы двух других чисел простого сообщения: 6=4+2. Перечисленные свойства простого сообщения называются существенными признаками. Простое сообщение, в котором причинный опорный термин имеет направленность на уменьшение первоначального числа объектов, обладает перечисленными существенными признаками. Рассмотрим простое сообщение: «Было 7 карандашей, из них отдали 2 карандаша. Осталось 5 карандашей». Причинный опорный термин – отдали – указывает на уменьшение первоначального числа карандашей. Значит, в этом случае первоначальное число простого сообщения и есть его наибольшее число, а относящийся к нему опорный термин «было» есть главный опорный термин этого сообщения. Вспомогательный опорный термин в этом сообщении «осталось», а причинный – «отдали». Простое сообщение называется истинным, если оно обладает всеми его существенными признаками. Если же отсутствует хотя бы один из существенных признаков, то это сообщение называется ложным. Признаки истинности простого сообщения. 1. Состоит из трех предложений, в каждом из которых имеется по одному именованному числу и по одному опорному термину. 2. Наименования трех чисел одинаковы или их можно сделать одинаковыми (заменить обобщающим словом). 3. Из трех опорных терминов (причинный (ПОТ), главный (ГОТ), вспомогательный (ВОТ)) только один является главным опорным термином. Правила нахождения ГОТ: ü если причинный опорный термин имеет направленность на увеличение первоначального числа объектов множества, то главный опорный термин относится к измененному числу (это слово «стало»); ü если причинный опорный термин имеет направленность на уменьшение первоначального числа объектов множества, то главный опорный термин относится к первоначальному числу объектов (это слово «было»); 4. Главный опорный термин относится к наибольшему числу. 5. Наибольшее число равно сумме двух других (или составлено из двух других). Например, проверим, является ли истинным сообщение: На ветке было 2 воробья. Прилетело 3 синицы. Стало 5 птиц. Зададим следующие вопросы: 1. Имеется ли в простом сообщении три числа и три опорных термина? (Да, имеется три числа – 2, 3, 5 и три опорных термина – было, прилетело, стало) 2. Одинаковы ли именования трех чисел? (Нет, наименования разные (воробьи, синицы, птицы), но их можно заменить обобщающим словом – птицы.) 3. Какой из опорных терминов является главным? ( ГОТ – стало, так как ПОТ указывает на увеличение первоначального числа.) 4. Относится ли главный опорный термин к наибольшему числу? (Да, он относится к числу 5) 5. Равно ли наибольшее число сумме двух других? (Да, 5 = 2+3) Вывод: данное сообщение является истинным простым сообщением. Раскроем методику обучения решению задач. Мы отметили, что первый этап – подготовительный. На данном этапе детей знакомят с простым сообщением. Для удобства детей термины можно упростить: вместо словосочетания «простое сообщение» можно употреблять «математический рассказ», вместо слов «опорный термин» - ведущее слово. Для условного обозначения существенных признаков простого сообщения используется моделирование. Опишем цикл занятий по формированию у детей представлений о простом сообщении. 1 занятие. Цель занятия – ознакомление с математическим рассказом и его первым существенным признаком: состоит из 3 предложений, 3 чисел, по одному в каждом предложении. Воспитатель читает детям математический рассказ. Например, «В вазе было 3 гвоздики. В вазу добавили еще 2 гвоздики. В вазе стало 5 гвоздик». Говорит, что это не простой рассказ, а математический. Спрашивает, почему его так называют. (В рассказе есть числа). Сколько предложений в математическом рассказе? (Три) Повторите первое предложение. Повторите второе предложение. Третье предложение. Когда дети произносят предложения – воспитатель на доске записывает эти предложения с помощью принятых в русском языке обозначений:
Затем воспитатель спрашивает, сколько чисел в математическом рассказе? (3 числа). В процессе беседы модель дополняется условными обозначениями числа:
Для закрепления детям предлагаются различные рассказы как математические, так и не математические. Математические рассказы могут содержать как 3 числа, так больше или меньше чисел. Таким образом, кроме анализа правильных математических рассказов (истинных простых сообщений), дети выполняют анализ и неправильных, находят в них ошибки и по возможности исправляют. Детям предлагается также самостоятельно составить математические рассказы. 2 занятие. Цель занятия – ознакомление с математическим рассказом и его вторым существенным признаком: у всех чисел одинаковые наименования. Воспитатель читает математический рассказ: «На тарелке было 3 яблока. Мама положила еще 1 яблоко. На тарелке стало 4 яблока». Ведется беседа по описанным выше вопросам и строится модель этого рассказа. Затем воспитатель спрашивает: Какое слово идет за каждым числом? (Яблоко). За каждым числом идет одинаковое слово. Модель дополняется картинками с яблоком: В дальнейшем от иконических моделей (предметных картинок) переходят к более абстрактным, когда наименование у чисел обозначают одинаковыми геометрическими фигурами – квадратами или прямоугольниками.
Для закрепления детям предлагаются как правильные математические рассказы, так и неправильные. Например, «В коробке лежало 6 карандашей. Из нее взяли 1 ручку. В коробке осталось 5 резинок» и т.п. В процессе анализа выясняется, почему этот рассказ неправильный и предлагается детям исправить его так, чтобы он стал правильным. Также детям предлагается самостоятельно составить математические рассказы и сказать правильные они или нет. 3 занятие. Цель – ознакомление с математическим рассказом и его третьим и четвертым существенным признаком: в каждом предложении есть ведущее слово. Из трех ведущих слов только одно является главным. Главный опорный термин относится к наибольшему числу. Детям предлагается математический рассказ, в котором опорными терминами (ведущими словами) являются «было», «убрали», «осталось». Например, «На полке было 5 книг. Мама взяла одну книгу. На полке осталось 4 книги». С детьми проводится беседа: Сколько предложений в математическом рассказе? (Три) Повторите первое предложение, второе, третье предложение. На доске появляется модель. Затем воспитатель говорит, что в математических рассказах имеются специальные слова, которые имеют особое значение. С помощью этих слов сообщается смысл чисел в рассказе. Так, смысл числа 5 раскрыт в находящемся рядом слове «было», которое означает, что на полке находятся книги и важно, что книг было 5. Далее в рассказе сообщается, что с этим числом произошли изменения. Об этом изменении говорит слово «взяла». Оно находится около числа 1. Последнее число в рассказе – это 4, смысл этого числа раскрывается с помощью слова «осталось». Таким образом, в нашем рассказе слова «было», «убрали», «осталось» – главные, ведущие, опорные. Аналогично идет работа с тройкой слов «было», «добавили», «стало». Затем детям сообщается, что ведущее слово, которое раскрывает смысл самого большого числа в рассказе, называется главным опорным термином (ГОТ) или главным ведущим словом. Какое главное ведущее слово в нашем первом рассказе? (Было) Среди ведущих слов есть слова, указывающие на то событие, которое произошло с предметами, названными в рассказе. Например: убрали, добавили, принесли, унесли и др. Такие слова называются причинными опорными терминами (ПОТ). И третье ведущее слово в задаче называется вспомогательным опорным термином (ВОТ). После этого построенная модель дополняется прямоугольниками разной длины
. . . Для закрепления детям предлагаются задания на анализ правильных и неправильных математических рассказов, составление моделей рассказов, а также задания на самостоятельное составление математических рассказов по моделям. 4 занятие. Цель – ознакомление с математическим рассказом и его пятым существенным признаком: наибольшее число составлено из двух других. Воспитатель читает математический рассказ. По этому рассказу проводится беседа: Сколько предложений в математическом рассказе? (Три) Повторите первое предложение, второе, третье предложение. На доске появляется модель. Назовите наибольшее число в рассказе. (Воспитатель записывает его на доске). Назовите другие числа в рассказе. Эти числа как-нибудь связаны между собой? (Да, наибольшее число составлено из двух других чисел или если мы к первому маленькому числу прибавим второе, то получим наибольшее число.) Для закрепления детям предлагаются задания на анализ различных математических рассказов, на составление моделей рассказов, а также задания на самостоятельное составление математических рассказов по моделям. На втором этапе детей знакомят с арифметической задачей и ее существенными признаками, учат решать задачи. Переход от математического рассказа к задаче происходит через замену в рассказе известного числа на неизвестное. Можно показать детям, что из верного математического рассказа получается 3 текста с одним неизвестным числом. Такие составленные рассказы Е.М. Семенов называет простыми задачами и выделяет следующие существенные признаки этого понятия: 1. Задача состоит из трех предложений, в ней имеются два известных числа и одно неизвестное и три опорных термина. 2. Наименования трех именованных чисел в задаче одинаковые. 3. Из трех ведущих слов только одно является главным опорным термином. 4. В задаче главный опорный термин относится к наибольшему числу. 5. Наибольшее число, состоит из двух других его чисел. Формирование перечисленных выше существенных признаков понятия «простая задача» происходит в течение нескольких занятий. Опишем фрагменты занятий, на которых у детей формируется представление о простой задаче. 1 занятие. В ходе выполнении этого задания выполняется наблюдение за текстом математического рассказа и простой задачи. Воспитатель предлагает математический рассказ: «На полке было 5 книг, к ним добавили 2 книги. На полке стало 7 книг». Затем проводится беседа: Сколько предложений в математическом рассказе? (Три) Сколько чисел в этом рассказе? (Три) Перечислите их. (5, 2, 7) Одинаковые ли наименования у чисел? (Да, одинаковые – книги.) Назовите главный опорный термин. (Стало) К какому числу относится ГОТ? (К наибольшему - 7) Из каких чисел состоит число 7? (Из чисел 5 и 2.) Сделайте вывод (Это верный (правильный) математический рассказ). Изменим этот рассказ так, чтобы в нем был нарушен признак «3 известных числа», чтобы одно из чисел стало неизвестным. Рассказ 1. Было 5 книг, добавили 2 книги. Сколько книг стало? Рассказ 2. Было 5 книг, несколько книг добавили. Стало 7 книг. Сколько книг добавили? Рассказ 3. Было несколько книг, добавили 2 книги. Стало 7 книг. Сколько книг было? Далее выполняется сравнение первоначального рассказа с каждым новым рассказом. Полученные 3 рассказа, в каждом из которых 2 известных числа и 1 неизвестное, называются простыми задачами. Воспитатель показывает, как изменяется модель рассказа, когда он становится задачей: в том предложении, где есть неизвестное число, внутри кружка пишется знак вопроса. В задаче неизвестное число обозначается словом «Сколько?»
Воспитатель сообщает детям, что в задаче имеется две части – условие и вопрос. Условие – часть задачи, в которой описывается заданная ситуация, числовые данные этой ситуации и связи между ними. Вопрос – часть задачи, в которой описывается требование найти неизвестную величину (неизвестное число). Показывается модель задачи.
Условие Вопрос Для закрепления предлагается несколько простых задач, в которых дети должны выделить 2 известных числа и 1 неизвестное. Выделить условие и вопрос задачи. В процесс чтения задачи воспитатель показывает числа, записав их на доске или с помощью карточек с цифрами, составляет модели задач. 2 занятие. Детям предлагаются рассказы, не являющиеся задачами. Например, «На столе лежат 5 ручек. К ним добавили несколько ручек. Сколько ручек стало на столе?». По этому тексту проводится беседа: 1. Сколько известных чисел? 2. Сколько неизвестных чисел? 3. Будет ли этот рассказ задачей? Измените рассказ так, чтобы он стал задачей. 3 занятие. На данном занятии идет работа по ознакомлению детей с математическим смыслом опорных терминов. Детям предлагаются практические ситуации: «Положите перед собой 2 прямоугольника. Справа еще один. Сколько всего прямоугольников положили?» и т.п. 4 занятие. В ходе этого занятия выявляется отношение опорных терминов к числам задачи (известным или неизвестным). Например, детям предлагается задача: В букете было 3 гвоздики. К ним добавили 2 гвоздики. Сколько всего гвоздик стало в букете? После чтения задачи проводится беседа: ü Какие опорные термины в данной задаче? (Было, добавили, стало) ü Назовите главный опорный термин. (Стало, так как причинный опорный термин указывает на увеличение первоначального числа) ü К известному или неизвестному числу он относится? (К неизвестному.) ü Давайте решим эту задачу. Как найти, сколько всего гвоздик стало? (Дети практически решают задачу, решение задачи записывается на доске с помощью цифр и знаков.) Аналогично выполняется анализ еще 2-3 задач, и воспитатель подводит итог: Задачи, в которых главный опорный термин относится к неизвестному числу, решаются действием сложения. На следующем, 5 занятии проводится аналогичная работа, но рассматриваются ситуации, когда главный опорный термин относится к известному числу. Например, У Светы было 5 шариков. Один шарик она подарила Оле. Сколько шариков осталось у Светы? После чтения задачи проводится беседа: ü Какие опорные термины в данной задаче? (Было, подарила, осталось) ü Назовите главный опорный термин. (Было) ü К известному или неизвестному числу он относится? (К известному числу 5.) ü Давайте решим эту задачу. Как найти, сколько осталось шариков? (Дети практически решают задачу, решение задачи записывается на доске с помощью цифр и знаков.) Аналогично выполняется анализ еще 2-3 задач, и воспитатель подводит итог: Задачи, в которых главный опорный термин относится к известному числу, решаются действием вычитания. 6 занятие. На данном занятии показывается роль наименований у чисел задачи. Для выявления роли наименований у чисел задачи изменяются наименования. Если при этом изменении задача перестанет существовать, либо превратится в элементарную, либо для ее решения надо будет выполнить другое, по сравнению с первой, арифметическое действие, то роль наименований будет показана. С детьми выполняются следующие задания. Задание 1: На елку повесили 3 фонарика и 4 ореха. Сколько орехов повесили на елку? (Для решения задачи не надо выполнять арифметического действия.) Измените задачу так, чтобы ее надо было решить действием сложения. (1. Меняем вопрос - Сколько всего игрушек повесили? 2. Меняем наименования - Сначала повесили 3 ореха, потом еще 4 ореха. 3. Орехи заменяем фонариками.) Задание 2: Две девочки и три мальчика катались с горки. Как зовут этих детей? (Это неразрешимая задача (причина - наименования).) Измените задачу так, чтобы ее можно было решить. Детям предлагается еще несколько аналогичных задач, после этого делается вывод о роли наименований у чисел: если наименования у чисел разные, то задачу решить нельзя. На 7 занятии детей знакомят с алгоритмом решения задач: 1.Найти в задаче главный опорный термин. 2.Определить, к какому числу относится главный опорный термин – известному или неизвестному. 3. 4.Записать решение задачи. 5.Назвать ответ задачи. Детям для запоминания алгоритма можно предложить такую модель. На третьем этапе у детей закрепляется умение решать простые задачи. Приведем пример работы над задачей. Задача: В коробке было 5 карандашей, добавили еще 2 карандаша. Сколько карандашей стало в коробке? Для того чтобы выделить главный опорный термин, необходимо найти причинный опорный термин. В данной задаче причинный опорный термин – добавили, он указывает на увеличение первоначального числа, значит главный опорный термин – стало. Главный опорный термин относится к неизвестному числу. Применяем правило: если главный опорный термин относится к неизвестному числу, то задача решается сложением. Значит, задачу решаем действием сложения. Записываем решение задачи 5 + 2 = 7. Формулируем ответ: В коробке стало 7 карандашей. В процессе работы по мере усвоения детьми данного алгоритма, рассуждения можно сократить. Например, «У Оли было 8 конфет. Две конфеты она отдала Марине. Сколько конфет у нее осталось?». Анализ задачи: Главный опорный термин – было, относится к известному числу, задачу решаем действием вычитания. Данная методика помогает сформировать существенные признаки простой задачи и однозначно выбрать действие, с помощью которого решается задача. Методика обучения решению задач А.В. Белошистой, описана в учебном пособии «Формирование и развитие математических способностей дошкольников» (М., 2004). В данной методике для ознакомления детей с арифметической задачей также выделяется три этапа. 1 этап. Цель – учить детей моделировать различные ситуации (объединение множеств, удаление части множества, увеличение или уменьшение множества на несколько элементов, сравнение и т.д.) с помощью различной предметной наглядности символического характера (геометрические фигуры, счетные палочки и т.п.). Учить моделировать различные ситуации в виде графической схемы и читать составленную схему ситуации. Детям предлагаются различные ситуации. Например, «Сначала Маша сорвала 3 яблока. Затем еще 2 яблока». Задание: Сосчитайте, сколько у Маши стало яблок. Для этого обозначьте каждое сорванное яблоко счетной палочкой. Дети выкладывают сначала 3 палочки, затем еще 2. Считают общее количество и отвечают на вопрос, заданный в задаче. Для обучения детей моделированию ситуации в виде схемы предлагается следующее задание: У Мартышки день рождения. Чтобы не забыть, что нужно сделать, она попросила Попугая нарисовать ей план - что поставить на стол. Попугай нарисовал такой план:
Что это может означать? Где у попугая обозначены полки с посудой, а где стол? (3 чашки с одной полки и 1 чашку с другой полки поставили на стол. На столе стоит 4 чашки.)
Аналогично рассматривается ситуация на удаление из множества части. Например: «К Мартышке пришли в гости Удав и Слоненок. А потом с чашками что-то произошло. Попугай нарисовал такую картинку.
Что могло произойти? Что изображено? (Было 4 чашки. Две чашки унесли на кухню, две остались. Или: две – разбили, две – осталось.)
Стрелки на схеме моделируют направление и вид действия: сходящиеся стрелки указывают на объединение, расходящиеся - удаление части. На данных схемах однозначно не задано, какая часть удалена, а какая оставлена. На данном этапе это не существенно. В дальнейшем, когда один из элементов схемы заменится на знак вопроса (произойдет переход к задаче) станет однозначно понятно, что удалили и что надо найти. Полезно показать руками направление движения стрелок, чтобы дети осознавали смысл схемы, моделируя ее через движения рук. Для закрепления умения составлять схему ситуации, используются задания следующих видов: детям предлагается составить сюжетный рассказ по картинке и изобразить его с помощью схемы, либо предлагается готовая схема и дети должны составить рассказ по ней. Пример задания первого вида: составить рассказ и схему по картинке.
Пример задания второго вида: составить рассказ по схеме.
2 этап. Цель – учить детей выбирать соответствующие арифметические действия и составлять математические выражения в соответствии с ситуацией, заданной текстом. Познакомить со знаком «=» и математическим равенством. Например, детям предлагается ситуация: «Мартышка сорвала с одной пальмы 2 банана, а со второй – 4. Все бананы она сложила в корзину». Задание – составить выражение и объяснить выбор знака.
2 + 4 А сколько всего бананов? (6)
Следует составлять только выражения, а не равенства, т.к. важно объяснить выбор знака, а не получить результат. Результат может быть получен пересчетом. Другая ситуация: «Девочка купила 2 красных шарика, 3 зеленых и 4 синих.
Как составить выражение? (2 + 3 + 4) Почему выбрали сложение? Сколько всего шариков? (9) Для обучения соотнесению схематической и символической (математическое выражение) модели ситуации полезно выполнять задания вида: «Выбрать из данных схем подходящую к выражению и объяснить свой выбор».
Критерием выбора выражения является направление стрелок. К сумме подходит 1, 2, а остальные подходят к разности. При выполнении задания следует придерживаться следующей последовательности действий: сначала выбирается нужная по структуре схема. Затем в нее вставляются два числа в парные квадраты. Последним заполняется квадрат с результатом.
Затем идет работа по схеме: Что означает число 6? (Столько ромашек было на поляне.) Что означает число 2? (Столько ромашек сорвала девочка.) Что означает число 4? (Столько ромашек осталось). Сравните запись 6 – 2 и схему. (В записи не обозначено число 4.) В схеме мы обозначили число оставшихся ромашек, а в записи выражения нет. Можно продолжить эту запись и обозначить число оставшихся ромашек, для этого используется специальный знак. Его называют «знак равенства». Пишут так: 6 – 2 = 4. Говорят так: 6 минус 2 равно 4. Всю эту запись целиком называют «равенство» – по имени знака равенства, который в ней использован. С помощью 2-3 различных упражнений дети закрепляют новое понятие и запись. 3 этап. Цель – ознакомление детей с задачей и обучение решению задач при помощи приемов присчитывания и отсчитывания.
или
После рассмотрения составленных рассказов проводится беседа: Чем этот рассказ отличается от тех, что мы составляли раньше? (В схеме есть знак вопроса, рассказ заканчивается вопросом.) Педагог сообщает, что рассказ, заканчивающийся вопросом, отвечая на который, надо выполнить какое-то арифметическое действие (прибавить или отнять), называется задачей. (Следует отметить, что данное определение сформулировано весьма приблизительно в понятной для детей форме и не предназначено для заучивания.) Далее в процессе выполнения различных упражнений дети уточняют особенности задачи (ее отличие от загадки, например такой как, «Два кольца, два конца, а посередине гвоздик»). Педагог подводит детей к пониманию того, что в задаче предлагается проблемная ситуация, для разрешения которой надо выбрать арифметическое действие и затем, выполнив его, ответить на вопрос. Также уточняются представления детей о существенных признаках задачи – наличие двух известных чисел (детям предлагаются тексты с недостающими и лишними данными), наличие вопроса, для ответа на который требуется выполнить арифметическое действие (Например, «Мартышка нашла на грядке 4 спелых клубники и 2 зеленых. Поделилась она с попугаем?»), наличие одинаковых наименований у чисел задачи (Например, «На окне сидели голуби. Три воробья улетели. Сколько сорок осталось на окне?). Детей учат составлять схему и запись решения задачи на нахождение суммы и остатка. Например, рассмотрим работу над задачей «Удав нюхал цветы на поляне. Всего там расцвело 7 цветов. Пришел Слоненок и нечаянно наступил на 1 цветок. Сколько цветов теперь сможет понюхать Удав?» Воспитатель после чтения задачи спрашивает у детей, является ли текст задачей и просит составить ее схему.
При решении задач рекомендуется использовать прием работы со скрытой наглядностью, т.е. сначала наглядность предъявляется, сосчитывается, обозначается цифрами, а затем прячется (в коробку, в корзину, за ширму и т.п.). После этого в соответствии с сюжетом задания приступают к выбору действия, поясняя его. Например: На ветке сидело 6 мартышек. (Педагог выставляет мартышек и предлагает обозначить их количество цифрой.) Затем изображение задергивается занавеской и сообщается продолжение сюжета: - Одна упала. (Эту одну мартышку можно достать из-за занавески и поставить на незакрытую часть фланелеграфа.) - Обозначьте эту мартышку цифрой. (Теперь рядом с занавеской две карточки с цифрами: 6 и 1.) - Каким действием можно обозначить то, что мартышка упала с ветки? (Вычитанием). - Почему вы выбираете вычитание? Почему не сложение? (Мартышка упала с ветки, и теперь на ветке их будет меньше, значит, надо вычитать). Запись завершается постановкой карточки со знаком вычитания. Теперь на фланелеграфе выражение: 6 – 1. - Как найти его значение? Закончите запись. Какой знак нужно поставить, чтобы обозначить, что получилось 5 мартышек? (Знак равенства). Фиксируем равенство: 6 – 1 = 5. После этого занавеска отдергивается и детям предлагается проверить правильность ответа пересчетом. С помощью таких приемов формируется правильное представление о том, что в решении задачи главное – это поиск действия, и том, что решение задачи и ее проверка – это разные учебные действия. Приведенные фрагменты занятий представляют собой взаимосвязанный блок, поскольку в них последовательно рассмотрены взаимосвязанные понятия. Далее, используя данные образцы, педагог может самостоятельно составлять занятия на эту тему, подбирая и придумывая тексты заданий и задач. Таким образом, мы рассмотрели четыре методики обучения дошкольников решению задач. Можно отметить, почти во всех методиках условно выделяется три этапа: 1) подготовительный этап к обучению решению задач; 2) ознакомление с простой задачей и ее решением; 3) формирование умения решать простые задачи на сложение и вычитание. Первоначально во всех методиках рассматривается работа с математическим рассказом: дети по различным картинкам или смоделированным ситуациям составляют рассказы, содержащие числа, и описывают их с помощью схем, т.е. словесную формулировку рассказа переводят в графическую. Однако описанные методики отличаются способом обоснования выбора действия. Так, в методике А.М. Леушиной выбор действия определяется словами: «положили», «добавили» и т.п.- действие сложения, «убрали», «улетели» и т.п. - действие вычитание. В методике Н.И. Непомнящей используется выделение в задаче частей и целого и в зависимости от того, что неизвестно (часть или целое) выбирается действие, которым и решается задача. В методике Е.М. Семенова предлагается выделить главный опорный термин, который находится по определенным правилам, и определить к какому числу (известному или неизвестному) он относится и в зависимости от этого выбрать действие. В методике А.В. Белошистой по ситуации, рассмотренной в задаче, строится схема, на которой стрелки моделируют направление и вид действия: сходящиеся стрелки показывают объединение (действие сложения), расходящиеся стрелки – удаление части (действие вычитание). С нашей точки зрения, однозначно выбрать и обосновать действие позволяют методики Е.М. Семенова и Н.И. Непомнящей.
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
. . .
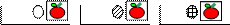
– ГОТ – главный опорный термин
– ПОТ – причинный опорный термин
– ВОТ – вспомогательный опорный термин
Применить правило: если главный опорный термин относится к неизвестному числу, то задача решается сложением. Если главный опорный термин относится к известному числу, то задача решается вычитанием.
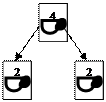
Дети могут составить такой рассказ: «На одной тарелке было 3 яблока, а на другой – 2 яблока. Мама сложила все яблоки в одну тарелку. В этой тарелке получилось 5 яблок». Схема выглядит следующим образом:
1) 2) 3) 4) 5)
Ознакомление детей с математическим равенством осуществляется в процессе рассмотрения следующей ситуации: «На полянке расцвело 6 ромашек (детям предлагается предметная наглядность). Девочка сорвала 2 ромашки, осталось 4. Составьте выражение» Дети составляют выражение 6 - 2. Затем подбирают к этому выражению схему и заполняют ее:
Введение понятия «задача» осуществляется в результате выполнения следующего задания: детям предлагается составить рассказ по новой схеме
Затем детям предлагается составить запись решения задачи. (7 - 1) Почему надо отнимать 1? (Слоненок наступил, поэтому цветов стало меньше. Стрелкой показали, что один из 7 цветков пропал.) Найдите ответ задачи. Запишите равенство. (7 – 1 = 6) Скажите ответ задачи. (Удав сможет понюхать 6 цветков.)