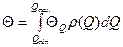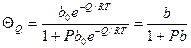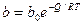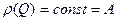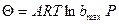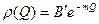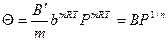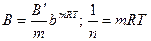|
|
Закон действующих поверхностейСкорость гетерогенно-каталитической реакции равна количеству вещества, реагирующего на единице поверхности катализатора за единицу времени
и зависит от степени заполнения поверхности молекулами реагентов. Вместо закона действующих масс в кинетике гетерогенного катализа используют закон действующих поверхностей: скорость элементарной химической реакции пропорциональна произведению поверхностных концентраций исходных веществ в степени, равной стехиометрическим коэффициентам, с которыми они входят в уравнение реакции (стадии). Поверхностную концентрацию обычно заменяют эквивалентной ей величиной – степенью заполнения поверхности данным реагентом Θ или доля занятой поверхности. Для мономолекулярной реакции
протекающей на поверхности катализатора
Для составления кинетического уравнения, очевидно, требуется уравнение для степени заполнения поверхности реагентом. Закон действующих поверхностей может быть использован при условии, что активные центры хаотически перемешаны и нет упорядоченной адсорбции. Уравнения адсорбции Уравнения для Θ выводятся из рассмотрения процессов адсорбции и десорбции. Для описания адсорбции используют модель образования мономолекулярного слоя на поверхности сорбента при адсорбции типа Т‒Г (твердый сорбент, газообразный адсорбат). Скорость адсорбции пропорциональна поверхности катализатора s, доле его свободной поверхности (1‒Θ) и парциальному давлению P адсорбата в газовой фазе:
Скорость десорбции пропорциональна поверхности сорбента и доле занятой поверхности:
При равновесии скорость адсорбции равна скорости десорбции
b = ka/kb – коэффициент адсорбции.
‒ вот такая форма уравнения изотермы адсорбции Ленгмюра, принятая для описания кинетики гетерогенного катализа. При низком давлении пара адсорбата уравнение Ленгмюра превращается в уравнение Генри:
При насыщении поверхностного слоя молекулами адсорбата все активные центры заняты адсорбированным веществом, Θ = 1. Степень заполнения веществом и количество молей сорбированного вещества связаны уравнением:
n∞ - максимальное количество адсорбированного вещества при Θ = 1, n - количество вещества, адсорбированного поверхностью Если на поверхности твердого тела адсорбируется смесь газов, то степень заполнения поверхности конкретным компонентом рассчитывается по уравнению:
n – количество компонентов в смеси. Следует помнить, что уравнение изотермы адсорбции Ленгмюра, хоть часто хорошо описывает адсорбцию на поверхности Т‒Г и Ж‒Г, было выведено в предположении а) однородной поверхности с равноценными активными центрами; б) образовании мономолекулярного слоя; в) идеальной системы, в которой отсутствует взаимодействие между сорбированными частицами. В реальном мире поверхность сорбента неоднородна, активные центры не равноценны и т.п. Неоднородность поверхности существенно влияет на равновесие и кинетические зависимости процесса адсорбции/десорбции. Модель Ленгмюра применима к очень небольшой доле поверхности с относительно однородными характеристиками. Для учета неоднородности поверхности используют т.н. распределение неоднородности и выполняется интегрирование по всем более-менее однородным участкам поверхности катализатора. Неоднородность определяется по теплоте адсорбции Q. С учетом распределения неоднородности уравнении для доли свободной поверхности:
ΘQ – доля заполненных мест поверхности с данной теплотой адсорбции; ρ(Q) - функция распределения адсорбционных мест по теплотам адсорбции. Если адсорбционные центры равномерно распределены по всем значениям теплот адсорбции, то функция распределения имеет вид:
При среднем заполнении поверхности адсорбатом работает модель (изотерма) Фрумкина-Темкина или логарифмическая изотерма:
bmax – коэффициент адсорбции при наибольшей теплоте адсорбции Если функция распределения экспоненциальная,
то при среднем заполнении поверхности адсорбатом работает модель (изотерма) Фрейндлиха:
В’ и m – коэффициенты. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
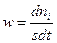
 ,
,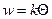
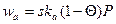
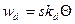
 или
или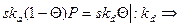
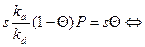

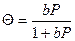
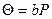
 ,
, ,
,