
|
|
Это уравнение получило название предельного закона Дебая-Хюккеля.Предельный закон устанавливает прямолинейную зависимость логарифма коэффициента активности от Сравнение с экспериментальными данными показывает, что предельный закон выполняется для довольно разбавленных растворов при ионной силе не более 0,001 М.
Зависимость lgγ± от ионной силы раствора для бинарного электролита (LiCl): 1 – предельный закон Дебая-Хюккеля, 2 – уравнение второго приближения; 3 – экспериментальная зависимость.
Картинка показывает сходимость эксперимента и расчета среднего ионного коэффициента. Во втором приближении теории Дебая-Хюккеля конечные размеры ионов учитываются с помощью параметра a, определяемого как среднее расстояние при максимальном сближении ионов. Однако точное значение величины а для растворов электролитов пока не возможно. Величину а поэтому рассматривают как эмпирическую константу, которая зависит от размера иона. Уравнение второго приближения имеет вид
где Аγ определяется соотношением
Коэффициент В для воды при 25°С равен 0,3287∙108 и мало зависит от температуры. Параметр а подбирают таким образом, чтобы расчетные данные совпадали с экспериментом. Порядок величины а – 1 нм. Уравнение второго приближения применимо до значения ионной силы 0,1. Для более широкого диапазона концентраций применяется уравнение третьего приближения Дебая-Хюккеля.
Которое учитывает уменьшение диэлектрической постоянной в непосредственной близости к иону. Величина коэффициента b – из эксперимента зависимости На основе теории Дебая-Хюккеля получены полуэмпирические уравнения:
Электрическая проводимость растворов Введение Электропроводность растворов электролитов, одно из самых общих свойств, является едва ли не наиболее хорошо и подробно изученным свойством. Сравнительно большая точность и легкость ее изучения давно привлекли внимание многочисленных исследователей, накопивших громадный экспериментальный материал. Однако, несмотря на это, до сих пор некоторые явления, связанные с электропроводностью, остаются непонятными и необъясненными теорией. Даже чрезвычайно сложная в математическом отношении современная теория электропроводности дает количественные соотношения, применимые лишь в области наиболее разбавленных растворов. Несмотря на то, что к настоящему времени опубликовано множество монографий и обзоров, посвященных этому вопросу, полной определенности проблема электрической проводимости в растворах так и не получила. Не удается описать с единых позиций концентрационную зависимость электропроводности в широком диапазоне концентраций, не совсем ясен механизм переноса электрической энергии в растворе, существуют разные подходы к интерпретации проводимости сильных и слабых электролитов. В основе экспериментального исследования явлений электропроводности лежит измерение величины удельного сопротивления раствора ρ, связанного с удельной электропроводностью уравнением:
Удельная электропроводность является функцией природы электролита, его концентрации, природы растворителя и температуры. В широком диапазоне концентраций удельная электропроводность проходит через максимум практически для всех электролитов. В разбавленных растворах (при концентрации C < 10−2 – 10−3 моль/л) наблюдается полное единообразие ‒ удельная электропроводность почти линейна по концентрации. Однако в концентрированных растворах, особенно в неводных растворах, такого единообразия не наблюдается. На начальном этапе исследований в области электрической проводимости растворов широко применялось правило Нернста-Томсона: диссоциирующая сила растворителя тем больше, чем больше его диэлектрическая проницаемость. Однако введение диэлектрической проницаемости в закон Кулона встречает существенное возражение – в микроскопическом объеме нельзя применять макроскопическую величину диэлектрической проницаемости. На очень большом опытном материале показано, что при соответствующем подборе компонентов раствора можно для любого растворителя (с малой или большой величиной диэлектрической проницаемости) найти такое вещество, которое образует с этим растворителем проводящий раствор. Некоторые из типичных сильных электролитов (например, галогеноводородные кислоты) совершенно не диссоциируют на ионы при растворении в HF; другие (большинство солей) вступают в реакции двойного обмена и, следовательно, не могут быть растворены как таковые в HF; третьи (кислоты) хотя и образуют с фтороводородной кислотой проводящие растворы, схема их диссоциации отличается от схемы в водных растворах. Эти экспериментальные факты обнаруживают слабость основных постулатов теории диссоциации и ионного переноса заряда. молярная электропроводность представляет собой отношение удельной электропроводности к концентрации электролита в 1 м3:
Молярная электропроводность равна проводимости раствора, содержащего 1 моль электролита, помещенного между параллельными электродами на расстоянии 1 м друг от друга. Если концентрация выражена не в молях на кубический метр, а в молях на литр, то в числителе следует ставить множитель 10-3:
На практике значительно чаще используют эквивалентную электропроводность, поскольку она исключает влияние заряда иона:
где z - число эквивалентов в 1 моле. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 . Из выражения предельного закона также следует, что чем меньше произведение εT, тем больше угловой коэффициент этой зависимости. Так, например, для воды при 25°С А = 0,51, для метанола – 1,78; для ацетона – 3,76.
. Из выражения предельного закона также следует, что чем меньше произведение εT, тем больше угловой коэффициент этой зависимости. Так, например, для воды при 25°С А = 0,51, для метанола – 1,78; для ацетона – 3,76.
 ,
, ,
, 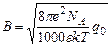
 ,
,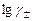 от концентрации.
от концентрации.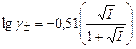 ,
, .
. , Ом‒1см‒1
, Ом‒1см‒1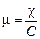

 ,
,