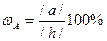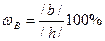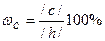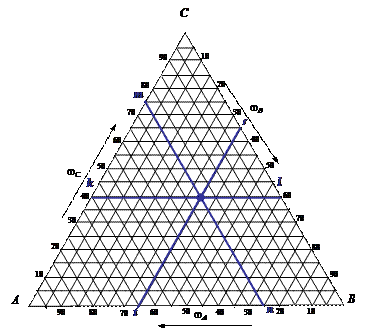
Трехкомпонентные конденсированные системы

Свойства трехкомпонентных систем определяются в общем случае четырьмя независимыми переменными: двумя внешними (давление и температура) и двумя переменными, характеризующими содержание любых двух компонентов из трех в процентах или долях единицы, т.е. состав системы. Если давление в системе постоянно, число переменных уменьшается до трех (состав и температура) и тогда диаграмма состояния трехкомпонентной системы может быть построена в трехмерном пространстве.

Состав трехкомпонентных систем, т.е. концентрация компонентов, графически изображается на плоскости (рис.71). С этой целью обычно используют равносторонний треугольник, называемый концентрационным, в вершинах которого располагаются чистые компоненты (К = 1), на каждой из его сторон - двухкомпонентные системы, а точки внутри треугольника соответствуют трехкомпонентным системам. С помощью сетки в треугольнике и чисел на его сторонах, характеризующих процентное содержание, нетрудно определить состав соответствующих каждой стороне двухкомпонентных систем и любой трехкомпонентной системы.

Виды концентрационных треугольников

Треугольник Гиббса

Применяется чаще для описания водно-солевых систем. Основан на свойстве равносторонних треугольников:

сумма длин перпендикуляров, опущенных из любой точки внутри равностороннего треугольника, равна высоте этого треугольника.

Треугольник Гиббса

Для построения диаграммы по методу Гиббса

проводят высоты из вершин треугольника;

каждую высоту делят на 10 – 100 равных частей;

через каждую точку деления проводят линии, параллельные сторонам треугольника.

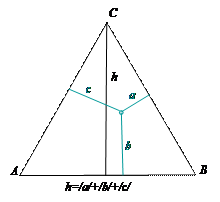
Определение состава системы по методу треугольника Гиббса

Чтобы определить состав системы по методу Гиббса нужно из заданной точки опустить перпендикуляры к сторонам треугольника. Содержание компонента будет определяться длиной перпендикуляра, противоположного вершине треугольника, соответствующей 100% содержанию этого компонента.

Так относительное количество компонента А определяется длиной отрезка а:

Относительное количество компонента В определяется длиной отрезка b:

Относительное количество компонента С определяется длиной отрезка с:

Длины отрезков a, b и c можно просто померить линейкой.

Метод Розебума

При этом используется одно из свойств концентрационного треугольника, согласно которому любая прямая, параллельная его стороне, есть геометрическое место точек с постоянным содержанием компонента, расположенного в вершине, противолежащей этой стороне.

При построении диаграммы по методу Розебума

строят равносторонний треугольник;

каждую сторону треугольника делят на 10 – 100 частей;

через тоски деления проводят линии, параллельные сторонам треугольника;

вершины треугольника – 100% содержание компонентов.

Треугольник Розебума

Определить состав системы по методу треугольника Розебума можно, например, так.

Выбрать точку внутри треугольника (точка Р).

Провести через эту точку две прямые, параллельные двум сторонам треугольника, например, (mn) и (kl).

Линия (mn) проходит через стороны треугольника, идущие от угла «А», следовательно, она определяет концентрацию компонента А – точка пересечения со стороной АС или АВ.

Линия (kl) проходит через стороны треугольника, идущие от угла «С», следовательно, она определяет концентрацию компонента С – точка пересечения со стороной СА или СВ.

Содержание третьего компонента можно определить по разности или

провести еще одну линию, параллельную стороне АС – линия (rt), пересекающая стороны треугольника, идущие из вершины В – она будет определять концентрацию компонента В в точка пересечения со стороной ВА или ВС.

Определение состава системы мо методу треугольника Розебума

Правило луча

Другим важным свойством концентрационного треугольника является «правило луча», в соответствии с которым любая прямая (луч), проведенная из вершины треугольника, есть геометрическое место точек с постоянным отношением концентраций двух противолежащих компонентов. Например, в точках 1, 2 и 3, лежащих на луче, проведенном из вершины треугольника А (рис.71), отношение концентраций компонентов В и С постоянно и равно 2/1, причем по мере удаления точки от вершины А по лучу содержание компонента А в трехкомпонентной системе уменьшается, а содержание компонентов Б и С растет. Это правило применяется для определения изменения состава жидкой фазы, насыщенной одним из компонентов (в данном случае компонентом А).

Третья переменная, температура, изображается на осях, проведенных из вершин концентрационного треугольника перпендикулярно его плоскости. В результате объемная диаграмма состояния трехкомпонентной системы представляет собой трехгранную призму, ребра которой характеризуют состояние каждого из трех компонентов и одновременно являются осями температуры, а грани – состояние трех соответствующих бинарных систем АВ, АС и ВС. Геометрические элементы внутри призмы отражают состояние трехкомпонентной системы.

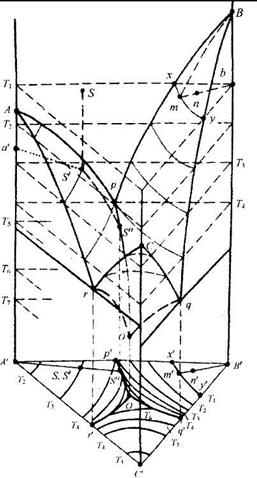
На рис. изображена объемная диаграмма состояния простейшей трехкомпонентной системы, компоненты которой неограниченно растворимы в жидком состоянии, кристаллизуются из расплава в чистом виде (твердых растворов нет), не образуют между собой химических соединений и не испытывают полиморфных превращений.

Точки А, В и С на этой диаграмме соответствуют температуре кристаллизации (или плавления) компонентов системы. Из этих точек берут начало по две линии ликвидус, расположенные на гранях призмы бинарных систем и пересекающиеся в точках двойных эвтектик р, q, r. В трехкомпонентной системе каждая пара этих линий служит границей поверхностей, показывающих, как и ликвидус бинарных систем, температуру начала кристаллизации одного из компонентов, соответственно А, В или С, а также состав жидкой фазы, насыщенной этим компонентом.

Точкам двойных эвтектик р, q и г в трехкомпонентной системе соответствуют линии двойных эвтектик рО, qO и rO, показывающие изменение состава жидкой фазы, насыщенной двумя компонентами (соответственно А и В, В и С, А и С) и являющиеся линиями пересечения каждой из двух поверхностей ликвидус. Точка О, расположенная на пересечении трех линий двойных эвтектик, соответствует наименьшей температуре на внешней поверхности диа­граммы и называется точкой тройной эвтектики. Она пока­зывает состав жидкой фазы, насыщенной одновременно тремя компонентами.

Основой топологии диаграммы является правило фаз Гиббса: F = К + п - Ф или при постоянном давлении F = 3 + 1 – Ф. Его следствия для трехкомпонентных систем:

одна фаза, например жидкая, имеет три степени свободы,т.е. одновременно могут меняться ее состав и температура, и поэтому ей соответствует определенный объем диаграммы;

две находящиеся в равновесии фазы имеют две степени свободы,т.е. переменный при заданной темпера туре состав, чему на объемной диаграмме соответствует поверхность, а на плоской диаграмме - линия;

три находящиеся в равновесии фазы обладают только одной степенью свободы(может меняться их температура) и поэтому при заданной температуре состав этих фаз строго фиксирован. Например, при кристаллизации из жидкости двойной эвтектики температура продолжает понижаться, но при этом состав эвтектической жидкости меняется по линии пересечения соответствующих поверхностей ликвидус;

если в равновесии находятся четыре фазы, а такое число фаз согласно правилу фаз Гиббса является максимальным, то система становится безвариантной.Этому состоянию системы на объемной диаграмме соответствует параллельная основанию призмы плоскость, на которой расположены фигуративные точки фаз постоянного состава, находящихся в равновесии при соответствующей постоянной температуре.

Например, при температуре Tq (рис.72), соответствующей точке тройной эвтектики О, число степеней свободы F = 0 и из жидкости, насыщенной тремя компонентами, происходит совместная кристаллизация этих компонентов по уравнению Ж₀ = А + В + С. Температура остается постоянной до тех пор, пока не закончится кристаллизация.

Изометрическая проекция объемной диаграммы, хотя и наглядна, но неудобна. На практике обычно используют плоские диаграммы в концентрационном треугольнике по Гиббсу или Розебуму, которые являются

а) сечением объемной диаграммы при заданной температуре;

б) проекцией нескольких сечений при разных температурах.

Не нашли, что искали? Воспользуйтесь поиском по сайту: