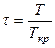|
|
Зависимость химического потенциала от температурыЗависимость химического потенциала от температуры для чистого вещества (в данном примере – растворителя), будучи представлена графически, имеет три кривые, соответствующие твердому, жидкому и газообразному состояниям.
Поскольку Точка А характеризуется фазовым переходом – плавлением растворителя; ей соответствует температура плавления Тm. Точка В соответствует процессу испарения с температурой кипения Ткип. Химический потенциал растворителя при образовании раствора, в соответствии с теорией идеальных растворов, понижается на величину Химический потенциал в газах Ситуация идеального газа Для начала рассмотрим ситуацию, когда есть идеальный газ – чистое вещество. В этой ситуации химический потенциал идеального газа равен его энергии Гиббса: Энергия Гиббса является функцией давления, температуры и состава. Т.к. взято чистое вещество, то
Ограничим систему по температуре (T = const). Тогда
Применив уравнение Менделеева-Клапейрона
где μ* – постоянная интегрирования. Для определения μ* используют представление о т.н. стандартном состоянии (P = 1 атм., Т = 298 K) С учетом стандартного состояния уравнение химического потенциала:
где Изменение химического потенциала
Если будет смесь идеальных газов, то для компонента смеси:
Химический потенциал реального газа В ситуации реального газа необходим учитывать взаимодействие молекул газа друг с другом. Взаимодействие не обязательно химическое. Может определяться электростатическим и другими видами взаимодействия молекул. Для учета взаимодействий молекул друг с другом Льюис предложил использовать понятие фугитивности в уравнении химического потенциала идеального газа:
В обоих уравнениях Изменение химического потенциала неидеального газа:
Фугитивность По Льюису фугитивность – величина, которую нужно подставить в выражение химического потенциала идеального газа, чтобы получить значение химического потенциала для реального газа. Величина фугитивности связана с парциальным давлением газа уравнением:
где Р – давление газа, γ – коэффициент фугитивности. Таким образом, величина фугитивности f включает в себя понятие концентрации (для газов – парциальное давление) и поправку на неидеальность системы γ. Фугитивность имеет такую же размерность, как и давление. Ее величина не зависит от размерности давления. Коэффициент фугитивности величина безразмерная, величина коэффициента фугитивности в одних и тех же условиях состояния газа зависит от единиц измерения. Обычно коэффициент фугитивности меньше единицы. При увеличении давления газа коэффициент фугитивности уменьшается до какого-то предела, но затем может и увеличиваться. При больших давлениях, когда силы притяжения преобладают над силами отталкивания, коэффициент фугитивности может быть больше единицы. К использованию фугитивности на практике прибегают при давлениях в системе, больших 50 атм. При меньших давлениях при выполнении приближенных вычислений, определением фугитивности пренебрегают. Для нахождения фугитивности необходимы данные до парциальному давлению и коэффициенту фугитивности. Коэффициент фугитивности определяют по экспериментальным данным. С использованием справочных данных коэффициент активности можно определить, например, по методу соответственных состояний. Принцип соответственных состояний: при одинаковых параметрах все газы обладают приблизительно одинаковыми свойствами. Приведенный параметр – это отношение данного параметра (давления, температуры) к его критическому значению. Приведенное давление Приведенная температура Критические значения температуры и давления приводятся в справочной литературе. Для определения коэффициента фугитивности пользуются специальными таблицами: 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
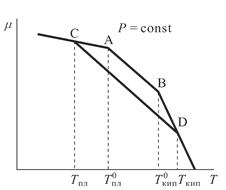
 , а S(s) < S(l) < S(g), то углы наклона касательных к зависимости
, а S(s) < S(l) < S(g), то углы наклона касательных к зависимости  будут увеличиваться по мере повышения температуры (энтропия зависит от температуры), а в точках фазового перехода претерпевать изломы, так как при этом энтропия меняется скачком.
будут увеличиваться по мере повышения температуры (энтропия зависит от температуры), а в точках фазового перехода претерпевать изломы, так как при этом энтропия меняется скачком.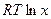 . Поэтому кривая
. Поэтому кривая  и адекватны экспериментальным данным для реальных растворов.
и адекватны экспериментальным данным для реальных растворов. .
. и ее изменение описывается дифференциальным уравнением:
и ее изменение описывается дифференциальным уравнением: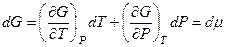
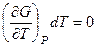 и с учетом свойства энергии Гиббса как характеристической функции
и с учетом свойства энергии Гиббса как характеристической функции  изменение химического потенциала определяется дифференциальным уравнением:
изменение химического потенциала определяется дифференциальным уравнением:
 для 1 моль газа и подставив полученное выражение для V в дифференциальное уравнение химического потенциала идеального газа получим:
для 1 моль газа и подставив полученное выражение для V в дифференциальное уравнение химического потенциала идеального газа получим: откуда
откуда 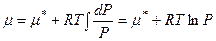 ,
,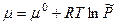 ,
, – стандартный химический потенциал,
– стандартный химический потенциал,  – относительное давление;
– относительное давление;  – отношение текущего парциального давления идеального газа к его давлению в стандартных условиях. Относительное давление – величина безразмерная, но численно относительное давление равно парциальному давлению газа, выраженному в атмосферах.
– отношение текущего парциального давления идеального газа к его давлению в стандартных условиях. Относительное давление – величина безразмерная, но численно относительное давление равно парциальному давлению газа, выраженному в атмосферах.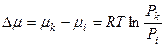
 и
и 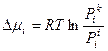
 для однокомпонентной системы
для однокомпонентной системы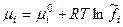 для смеси неидеальных газов
для смеси неидеальных газов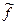 =1, а f0 = Р0);
=1, а f0 = Р0);  , где f0 – стандартная фугитивность – фугитивность газа в стандартном состоянии, относительная фугитивность численно равна фугитивности, выраженной в атмосферах.
, где f0 – стандартная фугитивность – фугитивность газа в стандартном состоянии, относительная фугитивность численно равна фугитивности, выраженной в атмосферах. для однокомпонентной системы
для однокомпонентной системы для смеси неидеальных газов
для смеси неидеальных газов ,
,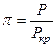 ;
;