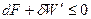|
|
Термодинамические потенциалыИз уравнения I и II начал термодинамики На практике используются системы закрытые либо открытые. Следовательно, необходим вывод критерия, который бы отвечал двум требованиям: 1) позволял прогнозировать направление протекания процесса в любых условиях его проведения; 2) его можно было вычислить исходя из термодинамических характеристик системы. В качестве подобного критерия была разработана система термодинамических потенциалов (Гиббс, Гельмгольц, Дюгем). Термодинамический потенциал – максимальная работа, которую может совершить система при обратимом протекании процесса в данных условиях. Тогда если система совершает по ходу процесса работу, меньшую, чем максимальная, то такой процесс идет самопроизвольно: Объединенное уравнение первого и второго законов термодинамики можно записать в виде для простой системы для сложной системы В простой системе осуществляются обратимые процессы: В сложной системе осуществляются обратимые процессы: Для систем, единственным видом работы которых является работа расширения (простые системы) четыре вида условий взаимодействия системы с окружающей средой:
Ситуация V,S = const Объединенное уравнение первого и второго законов термодинамики для простой системы: Очевидно, что для протекания процесса необходимо условие В данном случае внутренняя энергия будет термодинамическим потенциалом (изохорно-изоэнтропийным) и критерием возможности самопроизвольности протекания процесса. Ситуация Р,S = const Согласно преобразованию Лежандра Для простых систем Тогда уравнение Очевидно, что для протекания процесса необходимо условие В данном случае энтальпия будет термодинамическим потенциалом (изобарно-изоэнтропийным) и критерием возможности самопроизвольности протекания процесса. Ситуация V,T = const
Термодинамическая функция F=U – TS называется функцией Гелъмголъца, или изохорно-изотермическим потенциалом. Поскольку эта функция образована из функций состояния U и S, она также является функцией состояния. Очевидно, что для протекания процесса необходимо условие Таким образом с приближением системы к состоянию равновесия изохорно-изотермический потенциал убывает, достигая минимума в состоянии равновесия. Ситуация Р,T = const Р,T = const, следовательно W = 0.
Термодинамическая функция G = H – TS называется функцией Гиббса, или изобарно-изотермическим потенциалом. Поскольку эта функция образована из функций состояния U и S, она также является функцией состояния. Очевидно, что для протекания процесса необходимо условие Для сложных систем в перечисленных ситуациях критерии самопроизвольности протекания процесса те же самые. Преобразования уравнения V,S = const
В состоянии равновесия работа равна убыли внутренней энергии V,T = const
В состоянии равновесия работа равна убыли энтальпии V,T = const
В состоянии равновесия работа равна убыли энергии Гельмгольца Р,T = const
В состоянии равновесия работа равна убыли энергии Гиббса Функции U, H, F, G называются характеристическими. Работа, которая может быть совершена сложной системой при данных условиях взаимодействия с окружающей средой (за вычетом работы расширения), равна убыли соответствующих характеристических функций. Поскольку в состоянии равновесия работа, совершенная системой, максимальна при определенных внешних условиях, по этой причине характеристические функции U, И, F, G называют термодинамическими потенциалами. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 выводится, что для изолированных систем критерием самопроизвольности протекания процесса является изменение энтропии: dS > 0. Для состояния равновесия в изолированной системе нужно выполнение условия dS = 0.
выводится, что для изолированных систем критерием самопроизвольности протекания процесса является изменение энтропии: dS > 0. Для состояния равновесия в изолированной системе нужно выполнение условия dS = 0. или состояние равновесия
или состояние равновесия 





 , а для равновесия
, а для равновесия  .
.


 , а для равновесия
, а для равновесия  .
.
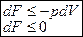
 , а для равновесия
, а для равновесия  .
.



 , а для равновесия
, а для равновесия 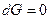 .
.